Thống kê Sinh học Cơ bản và Lâm sàng, Ấn bản thứ 5. Chương 10: Các Phương pháp Thống kê cho Nhiều Biến số (Thống kê Đa biến)

Thống kê Sinh học Cơ bản và Lâm sàng, Ấn bản thứ 5 – Basic & Clinical Biostatistics, 5e
Tác giả: Susan White – Nhà xuất bản McGraw-Hill Medical – Biên dịch: Ths.Bs. Lê Đình Sáng

Chương 10: Các Phương pháp Thống kê cho Nhiều Biến số
Statistical Methods for Multiple Variables

NHỮNG KHÁI NIỆM CHÍNH

Việc lựa chọn các phương pháp thống kê phụ thuộc vào câu hỏi nghiên cứu, các thang đo của biến số, và số lượng biến số cần phân tích.
Nhiều quy trình thống kê nâng cao có thể được diễn giải như một sự mở rộng hoặc sửa đổi của phân tích hồi quy đa biến.
Nhiều phương pháp thống kê được sử dụng cho các câu hỏi với một biến độc lập có sự tương đồng trực tiếp với các phương pháp cho nhiều biến độc lập.
Thuật ngữ “đa biến” (multivariate) được sử dụng khi có nhiều hơn một biến độc lập được phân tích.
Hồi quy đa biến là một phương pháp đơn giản và lý tưởng để kiểm soát các biến gây nhiễu.
Các hệ số hồi quy đa biến cho biết mối quan hệ giữa các biến độc lập và biến phụ thuộc là dương hay âm.
Mã hóa giả (dummy), hay chỉ báo (indicator), được sử dụng khi các biến danh nghĩa được dùng trong hồi quy đa biến.
Các hệ số hồi quy cho biết mức độ thay đổi của biến phụ thuộc cho mỗi thay đổi một đơn vị ở biến X, trong khi giữ hằng định các biến độc lập khác.
Hồi quy đa biến chỉ đo lường mối quan hệ tuyến tính.
Thống kê R đa biến (Multiple R) là chỉ số tốt nhất về mức độ phù hợp của mô hình với dữ liệu—mô hình giải thích được bao nhiêu phần trăm phương sai.
Có một số phương pháp có thể được sử dụng để lựa chọn các biến trong một hồi quy đa biến.
Hồi quy đa thức (Polynomial regression) có thể được sử dụng khi mối quan hệ là cong.
Kiểm định chéo (Cross-validation) cho chúng ta biết mô hình sẽ có khả năng áp dụng như thế nào nếu chúng ta sử dụng nó trên một mẫu đối tượng khác.
Một quy tắc kinh nghiệm tốt là có số đối tượng gấp mười lần số biến số.
Phân tích hiệp phương sai (Analysis of covariance) kiểm soát các biến gây nhiễu; nó có thể được sử dụng như một phần của phân tích phương sai hoặc trong hồi quy đa biến.
Hồi quy logistic (Logistic regression) dự đoán một kết cục danh nghĩa; đây là phương pháp hồi quy được sử dụng rộng rãi nhất trong y học.
Các hệ số hồi quy trong hồi quy logistic có thể được chuyển đổi để cho ra các tỷ số chênh (odds ratios).
Mô hình Cox (Cox model) là phương pháp tương tự đa biến của đường cong Kaplan-Meier; nó dự đoán các kết cục phụ thuộc thời gian khi có các quan sát bị kiểm duyệt.
Mô hình Cox còn được gọi là mô hình nguy cơ tỷ lệ thuận (proportional hazard model); đây là một trong những phương pháp thống kê quan trọng nhất trong y học.
Phân tích tổng hợp (Meta-analysis) cung cấp một cách để kết hợp các kết quả từ nhiều nghiên cứu một cách định lượng và đặc biệt hữu ích khi các nghiên cứu đi đến kết luận trái ngược nhau hoặc dựa trên các mẫu nhỏ.
Kích thước ảnh hưởng (Effect size) là một thước đo về độ lớn của sự khác biệt giữa hai nhóm; đây là một khái niệm hữu ích trong việc ước tính cỡ mẫu.
Bộ sưu tập Cochrane (Cochrane Collection) là một tập hợp các phân tích tổng hợp được thiết kế rất tốt và có sẵn tại các thư viện và trực tuyến.
Có một số phương pháp khả dụng khi mục tiêu là phân loại các đối tượng vào các nhóm.
Phân tích phương sai đa biến (Multivariate analysis of variance – MANOVA), tương tự như việc sử dụng ANOVA khi có nhiều biến phụ thuộc.

VẤN ĐỀ MỞ ĐẦU

Vấn đề mở đầu 1

Trong Chương 8, chúng ta đã xem xét nghiên cứu của Neidert và cộng sự (2016), nghiên cứu mối quan hệ giữa các phép đo thành phần cơ thể: hoạt độ DPP-IV huyết tương, mỡ gynoid, BMI, và khối lượng nạc.

Vấn đề mở đầu 2

Shah và cộng sự (2018) đã nghiên cứu các bệnh nhân bị tăng áp phổi (PHTN) để xác định xem tình trạng chức năng tự báo cáo của họ có thể được sử dụng để dự đoán các kết cục sau phẫu thuật hay không. Họ đã sử dụng hồi quy logistic để xác định những bệnh nhân có thể có thời gian nằm viện kéo dài (>7 ngày) dựa trên các chỉ số lâm sàng. Shah và các đồng nghiệp (2018) muốn phát triển một mô hình để giúp nhân viên bệnh viện dự đoán những bệnh nhân bị tăng áp phổi nào có thể có thời gian nằm viện sau phẫu thuật kéo dài.

Vấn đề mở đầu 3

Trong chương trước, chúng ta đã sử dụng dữ liệu từ một nghiên cứu của Lin và cộng sự (2018) để minh họa phương pháp phân tích sống còn Kaplan-Meier. Các nhà điều tra đã nghiên cứu hai phương pháp điều trị ung thư ruột kết di căn. Vui lòng tham khảo Chương 9 để biết thêm chi tiết.

MỤC ĐÍCH CỦA CHƯƠNG

Mục đích của chương này là trình bày một khung khái niệm áp dụng cho hầu hết tất cả các quy trình thống kê đã được thảo luận cho đến nay trong tài liệu này. Chúng tôi cũng mô tả một số kỹ thuật nâng cao hơn được sử dụng trong y học.

Một Khung Khái niệm

Các chương trước đã minh họa các kỹ thuật thống kê phù hợp khi số lượng quan sát trên mỗi đối tượng trong một nghiên cứu bị hạn chế. Ví dụ, phép kiểm t được sử dụng khi hai nhóm đối tượng được nghiên cứu và thước đo quan tâm là một biến số định lượng duy nhất—như trong Vấn đề mở đầu 1 ở Chương 6, thảo luận về sự khác biệt trong mức độ kích hoạt tự quản lý ở các đối tượng có và không có bệnh mãn tính (Bos-Touwen và cộng sự, 2015). Khi kết cục quan tâm là danh nghĩa, phép kiểm chi-bình phương có thể được sử dụng—như nghiên cứu của Anderson và cộng sự (2018) về vắc-xin cúm (Chương 6, Vấn đề mở đầu 3). Phân tích hồi quy được sử dụng để dự đoán một thước đo định lượng từ một thước đo khác, như trong nghiên cứu dự đoán tỷ lệ phần trăm mỡ cơ thể (Neidert và cộng sự, 2016; Chương 8, Vấn đề mở đầu 1).

Ngoài ra, mỗi ví dụ này có thể được xem xét về mặt khái niệm như là bao gồm một tập hợp các đối tượng với hai quan sát trên mỗi đối tượng: (1) đối với phép kiểm t, một biến định lượng, điểm kích hoạt, và một biến danh nghĩa (hoặc tư cách thành viên nhóm), bệnh tiểu đường loại II; (2) đối với phép kiểm chi-bình phương, hai biến danh nghĩa, vắc-xin cúm và chẩn đoán cúm sau khi có triệu chứng; (3) đối với hồi quy, hai biến định lượng, tỷ lệ phần trăm mỡ cơ thể và chỉ số khối cơ thể. Việc nhìn nhận các câu hỏi nghiên cứu từ góc độ này là có lợi vì các ý tưởng tương tự như các tình huống có nhiều biến số được bao gồm trong một nghiên cứu.

Để thực hành việc xem xét các câu hỏi nghiên cứu từ một góc độ khái niệm, chúng ta hãy xem lại Vấn đề mở đầu 1 trong Chương 7 của Dysangco và cộng sự (2017). Mục tiêu là để xác định xem có sự khác biệt về HCL-C ở những bệnh nhân HIV-, HIV+ có ART, và HIV+ không có ART hay không. Câu hỏi nghiên cứu trong nghiên cứu này có thể được xem là bao gồm một tập hợp các đối tượng với hai quan sát trên mỗi đối tượng: một biến định lượng, HDL-C, và một biến danh nghĩa (hoặc tư cách thành viên nhóm), tình trạng HIV, với ba loại. Nếu chỉ có hai loại được bao gồm cho tình trạng HIV, phép kiểm t sẽ được sử dụng. Tuy nhiên, với nhiều hơn hai nhóm, phân tích phương sai một chiều (ANOVA) là phù hợp.

Nhiều vấn đề trong y học có nhiều hơn hai quan sát trên mỗi đối tượng do sự phức tạp trong việc nghiên cứu bệnh tật ở người. Trên thực tế, nhiều vấn đề mở đầu được sử dụng trong tài liệu này có nhiều quan sát, mặc dù chúng tôi đã chọn đơn giản hóa các vấn đề bằng cách chỉ kiểm tra các biến số được chọn. Một phương pháp liên quan đến nhiều hơn hai quan sát trên mỗi đối tượng đã được thảo luận: ANOVA hai chiều. Nhớ lại rằng trong Vấn đề mở đầu 2 ở Chương 7, các hoạt động sinh hoạt hàng ngày (ADL) đã được kiểm tra ở các mức độ suy giảm nhận thức và giới tính khác nhau (Cornelis và cộng sự, 2017). Đối với phân tích này, các nhà điều tra đã phân loại các đối tượng theo hai biến danh nghĩa của suy giảm nhận thức—bệnh Alzheimer (AD) so với suy giảm nhận thức nhẹ (MCI) và giới tính—và một biến định lượng, chức năng ADL (i-ADL-CDI). Nếu thuật ngữ biến độc lập được sử dụng để chỉ các biến tư cách thành viên nhóm (ví dụ, AD hoặc MCI), hoặc biến X (ví dụ, huyết áp đo bằng thiết bị ngón tay), và thuật ngữ phụ thuộc được sử dụng để chỉ các biến có trung bình được so sánh (ví dụ, i-ADL-CDI), hoặc biến Y (ví dụ, huyết áp đo bằng thiết bị băng quấn), các quan sát có thể được tóm tắt như trong Bảng 10-1. (Để đơn giản, bản tóm tắt này bỏ qua các biến thứ tự; các biến được đo trên thang thứ tự thường được coi như là danh nghĩa.)

Bảng 10-1. Tóm tắt khung khái niệm cho các câu hỏi liên quan đến hai biến.

Biến độc lập	Biến phụ thuộc	Phương pháp
Danh nghĩa	Danh nghĩa	Chi-bình phương
Danh nghĩa (nhị phân)	Định lượng	Phép kiểm tª
Danh nghĩa (nhiều hơn hai giá trị)	Định lượng	ANOVA một chiềuª
Danh nghĩa	Định lượng (bị kiểm duyệt)	Phương pháp tính toán bảo hiểm
Định lượng	Định lượng	Hồi quyᵇ
ANOVA, phân tích phương sai.
ª Giả sử các giả định cần thiết (ví dụ, tính chuẩn, độc lập, v.v.) được đáp ứng. ᵇ Tương quan là phù hợp khi không có biến nào được chỉ định là độc lập hoặc phụ thuộc.

GIỚI THIỆU CÁC PHƯƠNG PHÁP CHO NHIỀU BIẾN SỐ

Các kỹ thuật thống kê liên quan đến nhiều biến số ngày càng được sử dụng nhiều trong nghiên cứu y học, và một số trong số chúng được minh họa trong chương này. Mô hình hồi quy đa biến, trong đó một số biến độc lập được sử dụng để giải thích hoặc dự đoán các giá trị của một biến phản hồi định lượng duy nhất, được trình bày đầu tiên, một phần vì nó là một sự mở rộng tự nhiên của mô hình hồi quy cho một biến độc lập được minh họa trong Chương 8. Tuy nhiên, quan trọng hơn, tất cả các phương pháp nâng cao khác ngoại trừ phân tích tổng hợp đều có thể được xem như là các sửa đổi hoặc mở rộng của mô hình hồi quy đa biến. Tất cả ngoại trừ phân tích tổng hợp đều liên quan đến nhiều hơn hai quan sát biến độc lập trên mỗi đối tượng và quan tâm đến việc giải thích hoặc dự đoán.

Mục tiêu trong chương này là trình bày logic của các phương pháp khác nhau được liệt kê trong Bảng 10-2 và minh họa cách chúng được sử dụng và diễn giải trong nghiên cứu y học.

Bảng 10-2. Tóm tắt khung khái niệm cho các câu hỏi liên quan đến hai hoặc nhiều biến độc lập (giải thích).

Các biến độc lập	Biến phụ thuộc	Phương pháp
Danh nghĩa	Danh nghĩa	Log-linear
Danh nghĩa và định lượng	Danh nghĩa (nhị phân)	Hồi quy logistic
Danh nghĩa và định lượng	Danh nghĩa (2 hoặc nhiều loại)	Hồi quy logistic, Phân tích phân biệtª, Phân tích cụm, Điểm xu hướng, CART
Danh nghĩa	Định lượng	ANOVAª, MANOVA
Định lượng	Định lượng	Hồi quy đa biếnª
Danh nghĩa và định lượng	Định lượng (bị kiểm duyệt)	Mô hình nguy cơ tỷ lệ thuận Cox
Các yếu tố gây nhiễu	Định lượng	ANCOVAª, MANOVAª, GEEª
Các yếu tố gây nhiễu	Danh nghĩa	Mantel-Haenszel
Chỉ định lượng		Phân tích nhân tố
CART, cây phân loại và hồi quy; ANOVA, phân tích phương sai; ANCOVA, phân tích hiệp phương sai; MANOVA, phân tích phương sai đa biến; GEE, phương trình ước tính tổng quát. ª Cần có một số giả định nhất định (ví dụ, tính chuẩn đa biến, độc lập, v.v.) để sử dụng các phương pháp này.

Trước khi chúng ta xem xét các phương pháp nâng cao, cần có một bình luận về thuật ngữ. Một số nhà thống kê dành riêng thuật ngữ “đa biến” (multivariate) để chỉ các tình huống liên quan đến nhiều hơn một biến phụ thuộc (hoặc phản hồi). Theo định nghĩa chặt chẽ này, hồi quy đa biến và hầu hết các phương pháp khác được thảo luận trong chương này sẽ không được phân loại là các kỹ thuật đa biến. Các nhà thống kê khác, bao gồm cả chúng tôi, cũng sử dụng thuật ngữ này để chỉ các phương pháp kiểm tra tác động đồng thời của nhiều biến độc lập. Theo định nghĩa này, tất cả các kỹ thuật được thảo luận trong chương này (có thể ngoại trừ một số phân tích tổng hợp) đều được phân loại là đa biến.

HỒI QUY ĐA BIẾN

Ôn tập về Hồi quy

Hồi quy tuyến tính đơn (Chương 8) là phương pháp được lựa chọn khi câu hỏi nghiên cứu là dự đoán giá trị của một biến phản hồi (phụ thuộc), ký hiệu là Y, từ một biến giải thích (độc lập) X. Mô hình hồi quy là:

Để đơn giản hóa ký hiệu trong chương này, chúng tôi sử dụng Y để chỉ biến phụ thuộc, mặc dù Y’, giá trị dự đoán, thực sự được cho bởi phương trình này. Chúng tôi cũng sử dụng a và b, các ước tính mẫu, thay vì các tham số quần thể, và , trong đó a là hệ số chặn và b là hệ số hồi quy. Vui lòng tham khảo Chương 8 nếu bạn muốn xem lại hồi quy tuyến tính đơn.

Hồi quy đa biến

Việc mở rộng hồi quy đơn sang hai hoặc nhiều biến độc lập là rất đơn giản. Ví dụ, nếu bốn biến độc lập đang được nghiên cứu, mô hình hồi quy đa biến là:

$X_{1}$ là biến độc lập thứ nhất và $b_{1}$ là hệ số hồi quy liên quan đến nó, $X_{2}$ là biến độc lập thứ hai và $b_{2}$ là hệ số hồi quy liên quan đến nó, và cứ thế tiếp tục. Phương trình số học này được gọi là một tổ hợp tuyến tính (linear combination); do đó, biến phản hồi Y có thể được biểu diễn dưới dạng một tổ hợp (tuyến tính) của các biến giải thích. Lưu ý rằng một tổ hợp tuyến tính thực sự chỉ là một trung bình có trọng số cho ra một con số duy nhất (hoặc chỉ số) sau khi các X được nhân với các b tương ứng của chúng và các tích bx được cộng lại.

Biến phụ thuộc Y phải là một thước đo định lượng. Mô hình hồi quy đa biến truyền thống cũng yêu cầu các biến độc lập phải là các thước đo định lượng; tuy nhiên, các biến độc lập danh nghĩa cũng có thể được sử dụng, như đã thảo luận trong phần tiếp theo. Tóm lại, kỹ thuật phù hợp cho các biến độc lập định lượng và một biến phụ thuộc định lượng duy nhất là mô hình hồi quy đa biến, như được chỉ ra trong Bảng 10-2.

Hồi quy đa biến có thể khó diễn giải, và kết quả có thể không lặp lại được nếu các biến độc lập có tương quan cao với nhau. Trong tình huống cực đoan, hai biến có tương quan hoàn hảo được gọi là cộng tuyến (collinear). Khi xảy ra đa cộng tuyến (multicollinearity), phương sai của các hệ số hồi quy lớn nên giá trị quan sát được có thể xa giá trị thực.

Diễn giải Phương trình Hồi quy Đa biến

Trong nghiên cứu của Neidert và cộng sự (2016) (Vấn đề mở đầu 1 trong Chương 8), mục tiêu của nghiên cứu là tổng hợp các thống kê liên quan đến BMI, tỷ lệ phần trăm mỡ cơ thể, và Dipeptidyl peptidase IV huyết tương cho những người khỏe mạnh. Chúng tôi cung cấp một số thông tin cơ bản về các biến này trong Bảng 10-3 và thấy rằng nghiên cứu bao gồm 71 nữ và 40 nam.

Bảng 10-3. Giá trị trung bình và độ lệch chuẩn phân theo giới tính.

Giới tính		Tuổi (năm)	BMI ( $k g / m^{2}$ )	% Mỡ
Nữ	Trung bình	24.63	23.39	32.28
	N	71	71	71
	Độ lệch chuẩn	8.82	3.80	6.54
Nam	Trung bình	27.20	24.54	21.36
	N	40	40	40
	Độ lệch chuẩn	10.85	3.69	7.84
Tổng	Trung bình	25.56	23.80	28.34
	N	111	111	111
	Độ lệch chuẩn	9.63	3.79	8.76
Dữ liệu từ Neidert LE, và cộng sự (2016).

Bảng 10-4 cho thấy phương trình hồi quy để dự đoán tỷ lệ phần trăm mỡ cơ thể. Tập trung ban đầu vào phần Hệ số, chúng ta thấy rằng tất cả các biến ngoại trừ tuổi đều có liên quan có ý nghĩa thống kê đến tỷ lệ phần trăm mỡ cơ thể.

Bảng 10-4. Hồi quy đa biến dự đoán tỷ lệ phần trăm mỡ cơ thể.

Tóm tắt Mô hình

Model	R	R Bình phương	R Bình phương Điều chỉnh	Sai số chuẩn của Ước tính
1	0,794ª	0,630	0,620	5,402703898
ª Các biến dự đoán: (Hằng số), Giới tính Nam, Tuổi (năm), BMI (kg/m²)

ANOVAª

Model		Tổng bình phương	df	Trung bình bình phương	F	Sig.
1	Hồi quy	5317,227	3	1772,409	60,721	,000ᵇ
	Phần dư	3123,245	107	29,189
	Tổng	8440,472	110
ª Biến phụ thuộc: % Mỡ ᵇ Các biến dự đoán: (Hằng số), Giới tính Nam, Tuổi (năm), BMI (kg/m²)

Hệ sốª

Model		Hệ số chưa chuẩn hóa		Hệ số chuẩn hóa
		B	Sai số chuẩn	Beta	t	Sig.
1	(Hằng số)	4,008	3,283		1,221	,225
	Tuổi (năm)	0,063	0,058	0,069	1,082	,282
	BMI (kg/m²)	1,142	0,148	0,494	7,705	,000
	Giới tính Nam	-12,389	1,083	-0,682	-11,439	,000
ª Biến phụ thuộc: % Mỡ
Nguồn dữ liệu: Neidert LE, và cộng sự (2016).

Biến thứ nhất là một biến định lượng, tuổi, với hệ số hồi quy, b, là 0,063, không có ý nghĩa thống kê ( $p = 0, 282$ ). Biến thứ hai, BMI, cũng là định lượng; hệ số hồi quy 1,142 cho thấy rằng những bệnh nhân có BMI cao hơn cũng có tỷ lệ phần trăm mỡ cơ thể cao hơn, điều này chắc chắn có lý.

Biến thứ ba, giới tính, là một biến nhị phân có hai giá trị. Đối với các mô hình hồi quy, việc mã hóa các biến nhị phân thành 0 và 1 là thuận tiện; trong ví dụ này, nữ có mã 0 cho giới tính, và nam có mã 1. Quy trình này, được gọi là mã hóa giả (dummy) hoặc chỉ báo (indicator), cho phép các nhà điều tra bao gồm các biến danh nghĩa trong một phương trình hồi quy một cách đơn giản. Các biến giả được diễn giải như sau: Một đối tượng là nam có mã cho nam, 1, được nhân với hệ số hồi quy cho giới tính, -12,389, dẫn đến việc trừ đi 12,389 điểm khỏi tỷ lệ phần trăm mỡ cơ thể của anh ta.

Các hệ số hồi quy được diễn giải khác nhau trong hồi quy đa biến so với hồi quy đơn. Trong hồi quy đơn, hệ số hồi quy b cho biết lượng giá trị dự đoán của Y thay đổi mỗi khi X tăng 1 đơn vị. Trong hồi quy đa biến, một hệ số hồi quy nhất định cho biết giá trị dự đoán của Y thay đổi bao nhiêu mỗi khi X tăng 1 đơn vị, trong khi giữ các giá trị của tất cả các biến khác trong phương trình hồi quy không đổi—như thể tất cả các đối tượng đều có cùng giá trị trên các biến khác.

Cần nhắc lại rằng hồi quy đa biến chỉ đo lường mối quan hệ tuyến tính giữa các biến độc lập và biến phụ thuộc, giống như trong hồi quy đơn. Biểu đồ phân tán giữa BMI và tỷ lệ phần trăm mỡ cơ thể được hiển thị trong Hình 10-1. Hình này cho thấy một mối quan hệ cong, và có thể phù hợp để biến đổi BMI bằng cách lấy logarit tự nhiên của nó.

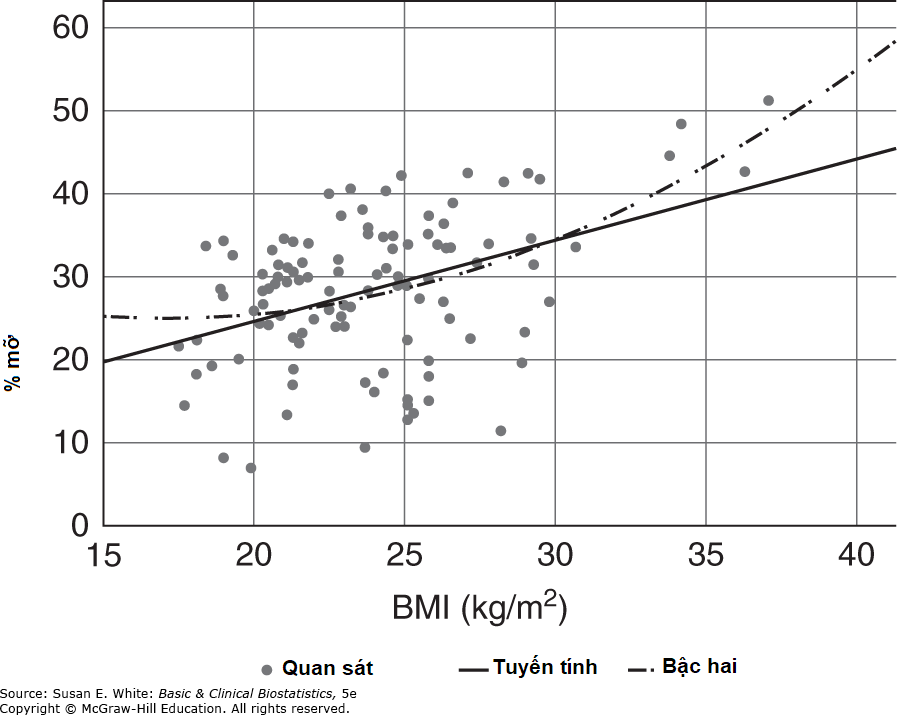
Hình 10-1. Biểu đồ minh họa mối quan hệ phi tuyến tính giữa BMI và tỷ lệ phần trăm mỡ cơ thể.

Hệ số hồi quy chuẩn hóa

Hầu hết các tác giả trình bày các hệ số hồi quy có thể được sử dụng với các đối tượng riêng lẻ để có được các giá trị Y dự đoán. Nhưng kích thước của các hệ số hồi quy không thể được sử dụng để quyết định biến độc lập nào là quan trọng nhất, bởi vì kích thước của chúng cũng liên quan đến thang đo mà các biến được đo lường, giống như trong hồi quy đơn. Các hệ số hồi quy này đôi khi được gọi là chưa chuẩn hóa (unstandardized); chúng không thể được sử dụng để đưa ra kết luận về tầm quan trọng của biến.

Một cách để loại bỏ ảnh hưởng của thang đo là chuẩn hóa (standardize) các hệ số hồi quy. Việc chuẩn hóa có thể được thực hiện bằng cách trừ đi giá trị trung bình của X và chia cho độ lệch chuẩn trước khi phân tích, để tất cả các biến có trung bình là 0 và độ lệch chuẩn là 1. Sau phép biến đổi này, có thể so sánh độ lớn của các hệ số hồi quy và đưa ra kết luận về biến giải thích nào đóng vai trò quan trọng. Các hệ số hồi quy chuẩn hóa thường được gọi là các hệ số beta (). Phần “Hệ số” của Bảng 10-4 cũng chứa các hệ số hồi quy chuẩn hóa. Sử dụng các hệ số chuẩn hóa trong Bảng 10-4, bạn có thể xác định biến nào, BMI hay giới tính, có ảnh hưởng nhiều hơn trong việc dự đoán tỷ lệ phần trăm mỡ cơ thể không? Nếu bạn chọn giới tính, bạn đã đúng, bởi vì giá trị tuyệt đối của hệ số chuẩn hóa của nó lớn hơn, 0,682, so với 0,494 của BMI.

Hệ số chuẩn hóa = hệ số chưa chuẩn hóa nhân với độ lệch chuẩn của biến X và chia cho độ lệch chuẩn của biến Y: .

R Đa biến

R đa biến (Multiple R) là sự tương tự trong hồi quy đa biến của hệ số tương quan moment sản phẩm Pearson r. Nó còn được gọi là hệ số xác định đa biến (coefficient of multiple determination). Ví dụ, giả sử tỷ lệ phần trăm mỡ cơ thể được tính cho mỗi người trong nghiên cứu của Niedert và cộng sự; sau đó, tương quan giữa tỷ lệ phần trăm mỡ cơ thể dự đoán và tỷ lệ phần trăm mỡ cơ thể thực tế được tính. Tương quan này là R đa biến. Nếu R đa biến được bình phương (), nó đo lường bao nhiêu phần trăm sự biến thiên trong điểm trầm cảm thực tế được giải thích bằng việc biết thông tin có trong phương trình hồi quy. được diễn giải theo cách hoàn toàn giống như trong tương quan và hồi quy đơn.

Sau khi BMI, tuổi và chủng tộc được nhập vào phương trình hồi quy, cho thấy rằng hơn 63% sự biến thiên trong tỷ lệ phần trăm mỡ cơ thể được giải thích bằng việc biết BMI, tuổi và chủng tộc của bệnh nhân.

Lựa chọn Biến cho Mô hình Hồi quy

Việc quyết định các biến cung cấp dự đoán tốt nhất đôi khi được gọi là xây dựng mô hình (model building). Việc lựa chọn các biến cho các mô hình hồi quy có thể được thực hiện theo nhiều cách.

Các chương trình máy tính cũng chứa các quy trình để chọn một tập hợp tối ưu các biến giải thích. Một quy trình như vậy được gọi là chọn tiến (forward selection). Chọn tiến bắt đầu với một biến trong phương trình hồi quy; sau đó, các biến bổ sung được thêm vào từng cái một cho đến khi tất cả các biến có ý nghĩa thống kê được bao gồm trong phương trình.

Một quy trình loại bỏ lùi (backward elimination) tương tự cũng có thể được sử dụng; trong đó, tất cả các biến ban đầu được bao gồm trong phương trình hồi quy. Biến X sẽ làm giảm đi một lượng nhỏ nhất sẽ được loại bỏ khỏi phương trình.

Khi các đặc điểm của cả hai quy trình chọn tiến và loại bỏ lùi được sử dụng cùng nhau, phương pháp này được gọi là hồi quy từng bước (stepwise regression).

Hồi quy Đa thức

Hồi quy đa thức (Polynomial regression) là một trường hợp đặc biệt của hồi quy đa biến trong đó mỗi số hạng trong phương trình là một lũy thừa của X. Hồi quy đa thức cung cấp một cách để phù hợp một mô hình hồi quy với các mối quan hệ cong và là một giải pháp thay thế cho việc biến đổi dữ liệu thành một thang đo tuyến tính. Ví dụ, phương trình sau có thể được sử dụng để dự đoán một mối quan hệ bậc hai:

Kiểm định chéo

Các quy trình thống kê cho tất cả các mô hình hồi quy dựa trên các tương quan giữa các biến, mà đến lượt nó, liên quan đến lượng biến thiên trong các biến được bao gồm trong nghiên cứu. Tuy nhiên, một số biến thiên quan sát được trong bất kỳ biến nào chỉ đơn giản là xảy ra do ngẫu nhiên. Nếu phương trình được sử dụng để dự đoán kết quả cho các đối tượng trong tương lai, nó nên được xác thực trên một mẫu thứ hai, một quá trình được gọi là kiểm định chéo (cross validation).

Yêu cầu về Cỡ mẫu

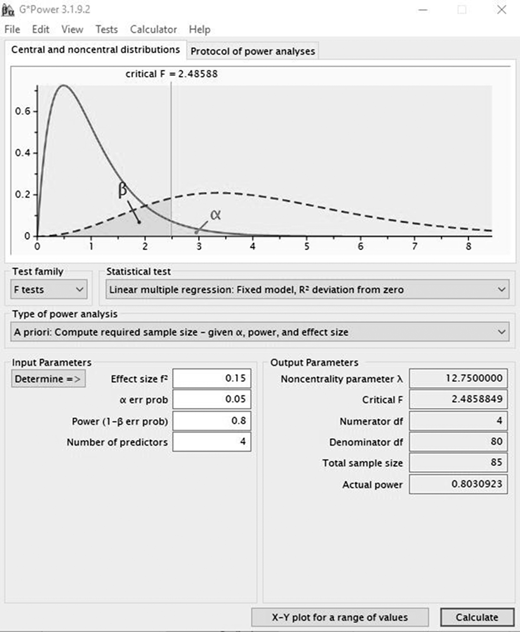
Một khuyến nghị phổ biến của các nhà thống kê yêu cầu số lượng đối tượng gấp mười lần số lượng biến độc lập. Hộp 10-1 cho thấy kết quả từ chương trình G*Power để ước tính cỡ mẫu. Phân tích công suất chỉ ra rằng một mẫu 85 người cho công suất là 0,80, giả sử giá trị $α$ hay p là 0,05.

HỘP 10-1. ƯỚC TÍNH CỠ MẪU CHO HỒI QUY ĐA BIẾN SỬ DỤNG GPOWER.*

KIỂM SOÁT SỰ GÂY NHIỄU

Phân tích Hiệp phương sai

Phân tích hiệp phương sai (Analysis of covariance – ANCOVA) là kỹ thuật thống kê được sử dụng để kiểm soát ảnh hưởng của một biến gây nhiễu. Các biến gây nhiễu xảy ra thường xuyên nhất khi các đối tượng không thể được phân ngẫu nhiên vào các nhóm khác nhau, tức là, khi các nhóm quan tâm đã tồn tại. Guo và cộng sự (2018) (Chương 7 và 8) đã dự đoán thể lực tổng thể được đo bằng dựa trên Chỉ số Ruffier (RI); họ muốn kiểm soát tuổi của các đối tượng và đã làm như vậy bằng cách thêm tuổi vào phương trình hồi quy. Khi chỉ RI được sử dụng để dự đoán thể lực ( tính bằng ), phương trình hồi quy là:

Phương trình có thêm tuổi là:

Sử dụng phương trình này, mức độ thể lực được dự đoán sẽ giảm 0,952 cho mỗi lần tăng 1 đơn vị RI, trong khi giữ tuổi không đổi hoặc độc lập với tuổi.

Trong ANCOVA, biến gây nhiễu được gọi là hiệp biến (covariate), và giá trị trung bình của biến phụ thuộc trong các nhóm được cho là đã được điều chỉnh (adjusted) theo hiệp biến. Hình 10-2 minh họa dữ liệu giả định, trong đó mối quan hệ giữa điểm tắc nghẽn và bất thường vận động thành tim dường như là như nhau đối với người hút thuốc và người không hút thuốc. Tuy nhiên, người không hút thuốc có cả điểm tắc nghẽn thấp hơn và số lượng bất thường vận động thành tim thấp hơn.

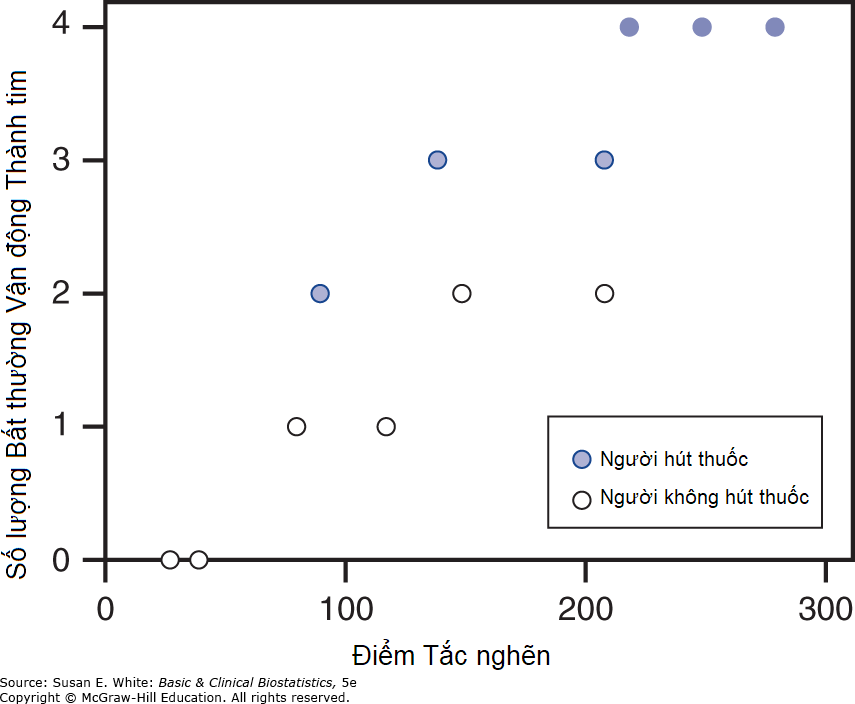
Hình 10-2. Mối quan hệ giữa mức độ hẹp động mạch vành và các bất thường vận động thành tâm thất ở người hút thuốc và người không hút thuốc (dữ liệu giả định).

Phương trình hồi quy được xác định cho các quan sát giả định trong Hình 10-2 là:

Nếu ANCOVA được sử dụng để kiểm soát mức độ hẹp động mạch vành, trung bình vận động thành tim đã điều chỉnh là 2,81 đối với người hút thuốc và 1,53 đối với người không hút thuốc, chênh lệch 1,28. Trong ANCOVA, trung bình Y đã điều chỉnh cho một nhóm nhất định được tính như sau:

$\bar{Y}_{\text{đã điều chỉnh, j}} = \bar{Y}_{\text{chưa điều chỉnh, j}} - b(\bar{X}_j - \bar{X}_{\text{chung}})$

Hình 10-3 minh họa một cách sơ đồ cách ANCOVA điều chỉnh trung bình của biến phụ thuộc nếu hiệp biến là quan trọng.

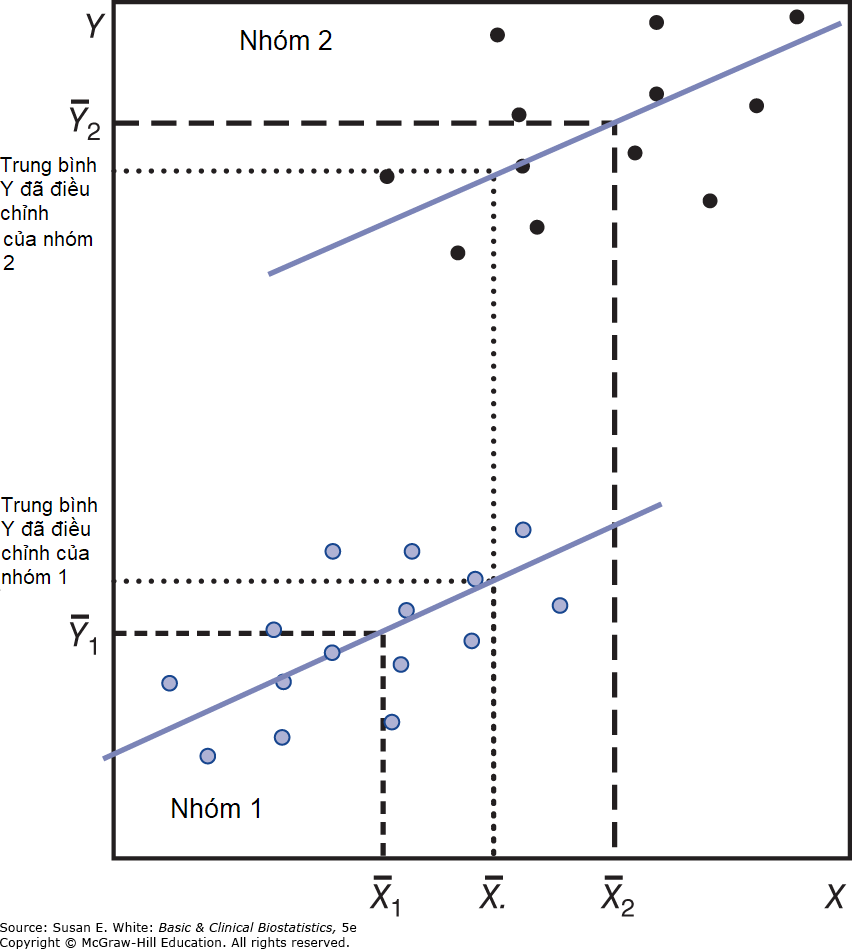
Hình 10-3. Minh họa các giá trị trung bình được điều chỉnh bằng phân tích hiệp phương sai.

ANCOVA giả định rằng mối quan hệ giữa hiệp biến (biến X) và biến phụ thuộc (Y) là như nhau trong tất cả các nhóm, tức là các độ dốc hồi quy là như nhau.

ANCOVA có thể được coi là một trường hợp đặc biệt của câu hỏi tổng quát hơn về việc so sánh hai đường hồi quy. Nếu chúng ta đặt X là BMI, Y là phần trăm mỡ cơ thể, và Z là một biến giả, trong đó Z=1 cho nam và Z=0 cho nữ, thì mô hình hồi quy đa biến để kiểm tra xem hai đường hồi quy có giống nhau không là:

Phương trình Ước tính Tổng quát (GEE)

Nhiều thiết kế nghiên cứu, bao gồm cả các nghiên cứu quan sát và thử nghiệm lâm sàng, liên quan đến các quan sát được phân cụm hoặc phân cấp. Một nhóm các phương pháp đã được phát triển cho những tình huống đặc biệt này. Ví dụ, trong một nghiên cứu, kết quả của những bệnh nhân được phẫu thuật bởi cùng một bác sĩ phẫu thuật có thể liên quan đến các yếu tố khác ngoài phương pháp phẫu thuật, chẳng hạn như trình độ kỹ năng của bác sĩ phẫu thuật. Trong tình huống này, bệnh nhân được cho là lồng vào (nested) trong các bác sĩ.

Nhóm các phương pháp phù hợp với các loại câu hỏi nghiên cứu này bao gồm phương trình ước tính tổng quát (generalized estimating equations – GEE), mô hình đa cấp, và phân tích dữ liệu có cấu trúc phân cấp.

DỰ ĐOÁN CÁC KẾT CỤC DANH NGHĨA HOẶC PHÂN LOẠI

Khi kết cục được đo trên thang danh nghĩa, các phương pháp tiếp cận khác phải được sử dụng. Bảng 10-2 chỉ ra rằng một số phương pháp có thể được sử dụng để phân tích các vấn đề với một số biến độc lập khi biến phụ thuộc là danh nghĩa.

Hồi quy Logistic

Hồi quy logistic (Logistic regression) thường được sử dụng khi các biến độc lập bao gồm cả các thước đo định lượng và danh nghĩa và biến kết cục là nhị phân (lưỡng phân). Mô hình logistic cho xác suất mà kết cục xảy ra như một hàm số mũ của các biến độc lập. Ví dụ, với ba biến độc lập, mô hình là:

trong đó $b_{0}$ là hệ số chặn, $b_{1}, b_{2}$ , và $b_{3}$ là các hệ số hồi quy, và exp cho biết rằng cơ số của logarit tự nhiên (2,718) được lũy thừa lên số mũ trong ngoặc.

Trong nghiên cứu được mô tả trong Vấn đề mở đầu 2, các biến được các nhà điều tra sử dụng để dự đoán thời gian nằm viện kéo dài được liệt kê trong Bảng 10-5. Kết quả phân tích được đưa ra trong Bảng 10-6.

Bảng 10-5. Các biến, mã, và tần số của các biến.ª

	Giá trị	Tần số
ASA
3	0	420
>3	1	130
Tình trạng chức năng kém
Không	0	277
Có	1	273
Tăng huyết áp nặng
Có	0	365
Không	1	185
Phương pháp phẫu thuật mở
Không	0	258
Có	1	292
Thời gian phẫu thuật
<= 2 giờ	0	350
>2 giờ	1	197
Tăng áp phổi nặng
Không	0	477
Có	1	50
ª Không phải tất cả các tổng đều giống nhau do thiếu dữ liệu trên một số biến. Dữ liệu từ Shah AC, và cộng sự (2018).

Bảng 10-6: Mô hình hồi quy Logistic cho LOS (Thời gian nằm viện) lớn hơn 7 ngày

Các biến trong phương trình

	B	S.E.	Wald	df	Sig.	Exp(B)	KTC 95% cho EXP(B)
							Dưới
Bước 1ª
ASA <=3; >3 (1)	0,887	0,240	13,717	1	,000	2,428	1,518
Tình trạng chức năng KÉM (1)	0,754	0,234	10,378	1	,001	2,126	1,344
KHÔNG có Tăng huyết áp nặng (1)	0,632	0,236	7,153	1	,007	1,882	1,184
Phương pháp phẫu thuật MỞ (1)	1,084	0,249	18,968	1	,000	2,957	1,815
Thời gian phẫu thuật <=2 / >2 (1)	0,838	0,230	13,271	1	,000	2,311	1,473
Hằng số	-3,246	0,305	113,039	1	,000	0,039

Bảng phân loạiᵇ

		Dự đoán
Quan sát		LOS > 7 ĐÚNG	Tỷ lệ phần trăm Đúng
		0	1
Bước 1	LOS > 7 ĐÚNG
	0	409	22
	1	90	26
	Tỷ lệ phần trăm Tổng thể

ª Các biến được nhập vào ở bước 1: ASA<=3/>3, Tình trạng chức năng KÉM, KHÔNG có Tăng huyết áp nặng, Phương pháp phẫu thuật MỞ, Thời gian phẫu thuật <=2/>2. ᵇ Giá trị ngưỡng là 0,500. Nguồn dữ liệu: Shah AC, và cộng sự (2018).

Cột trong Bảng 10-6 có nhãn “Exp(B)” là rủi ro tương đối cho giá trị 1 so với 0 cho mỗi yếu tố nguy cơ. Phương trình logistic có thể được sử dụng để tìm xác suất cho bất kỳ cá nhân nào. Ví dụ, chúng ta hãy tìm xác suất một bệnh nhân có ASA là 1, tình trạng chức năng kém, không có sHTN, và một thủ thuật phẫu thuật mở kéo dài 1 giờ có thời gian nằm viện dài hơn 7 ngày.

Các hệ số hồi quy từ Bảng 10-6 là:

và chúng ta đánh giá nó như sau:

Thay -0,776 vào phương trình xác suất:

Do đó, cơ hội bệnh nhân này có LOS dài là 31,5%.

Một ưu điểm của hồi quy logistic là hệ số hồi quy có thể được diễn giải dưới dạng rủi ro tương đối trong các nghiên cứu đoàn hệ hoặc tỷ số chênh trong các nghiên cứu bệnh-chứng. Ví dụ, rủi ro tương đối của LOS >7 sau một thủ thuật phẫu thuật kéo dài hơn 2 giờ là .

Phân tích Log-Linear

Khi cả biến độc lập và biến phụ thuộc đều được đo trên thang danh nghĩa, và có ba hoặc nhiều biến, một phương pháp thống kê gọi là phân tích log-linear là phù hợp. Phân tích log-linear tương tự như một mô hình hồi quy trong đó tất cả các biến, cả độc lập và phụ thuộc, đều được đo trên thang danh nghĩa. Kỹ thuật này được gọi là log-linear vì nó liên quan đến việc sử dụng logarit của các tần số quan sát được trong bảng ngẫu nhiên.

DỰ ĐOÁN MỘT KẾT CỤC BỊ KIỂM DUYỆT: MÔ HÌNH NGUY CƠ TỶ LỆ THUẬN COX

Trong Chương 9, chúng ta đã thấy rằng các phương pháp đặc biệt phải được sử dụng khi một kết cục chưa được quan sát cho tất cả các đối tượng trong mẫu nghiên cứu. Kỹ thuật hồi quy do Cox (1972) phát triển là phù hợp khi có các quan sát bị kiểm duyệt phụ thuộc thời gian. Kỹ thuật này được gọi là hồi quy Cox, hay mô hình nguy cơ tỷ lệ thuận.

Hiểu Mô hình Cox

Nhớ lại từ Chương 9 rằng hàm sống còn cho xác suất một người sẽ sống sót qua khoảng thời gian tiếp theo, với điều kiện họ đã sống sót cho đến thời điểm đó. Hàm nguy cơ, ngược lại, là xác suất một người sẽ chết trong khoảng thời gian tiếp theo, với điều kiện họ đã sống sót cho đến đầu khoảng thời gian đó.

Trong mô hình Cox, độ dài thời gian được đánh giá bằng hàm nguy cơ, và tổ hợp tuyến tính của các giá trị độc lập là số mũ của logarit tự nhiên, e. Ví dụ, đối với nghiên cứu của Martinez, mô hình được viết là:

Nói cách khác, mô hình này nói rằng xác suất chết trong khoảng thời gian tiếp theo có thể được tìm thấy bằng cách nhân nguy cơ cơ bản ( $h_{0}$ ) với logarit tự nhiên được nâng lên lũy thừa của tổ hợp tuyến tính của các biến độc lập.

Một ví dụ về Mô hình Cox

Trong nghiên cứu của Martínez và cộng sự (2017), các nhà nghiên cứu đã sử dụng mô hình nguy cơ tỷ lệ thuận Cox để kiểm tra mối quan hệ giữa tình trạng hôn nhân và sự sống còn do ung thư vú. Các nhà điều tra muốn kiểm soát các biến gây nhiễu có thể có. Kết quả phân tích từ Bảng 3 trong bản thảo, được sao chép trong Bảng 10-8, được sử dụng để chỉ ra một số đặc điểm nổi bật của phương pháp này.

Bảng 10-8. Kết quả từ mô hình nguy cơ tỷ lệ thuận Cox sử dụng cả các biến trước và sau điều trị.

	Tử vong toàn bộ
	Số ca tử vong Chưa kết hôn	Số ca tử vong Đã kết hôn	MRRª (KTC 95%) Chưa kết hôn vs. Đã kết hôn
Theo Chủng tộc/sắc tộc
Da trắng không phải gốc Tây Ban Nha	8761	5858	1.31 (1.26-1.36)
Da đen	1599	614	1.17 (1.05-1.30)
Gốc Tây Ban Nha	1943	1750	1.15 (1.07-1.24)
Châu Á/Đảo Thái Bình Dương	894	1006	1.29 (1.16-1.43)
Khác/không rõ	109	76	1.06 (0.74-1.53)
p-không đồng nhấtᵇ			<0.001
…
MRR là tỷ số suất tử vong (mortality rate ratios) và có thể được diễn giải giống như tỷ số nguy cơ.

PHÂN TÍCH TỔNG HỢP

Phân tích tổng hợp (Meta-analysis) là một cách để kết hợp kết quả của một số nghiên cứu độc lập về một chủ đề cụ thể. Phân tích tổng hợp khác với các phương pháp đã thảo luận ở các phần trước vì mục đích của nó không phải là để xác định các yếu tố nguy cơ hoặc dự đoán kết quả cho các bệnh nhân riêng lẻ; thay vào đó, kỹ thuật này có thể áp dụng cho bất kỳ câu hỏi nghiên cứu nào.

Sacks và cộng sự (1987) đã xem xét các phân tích tổng hợp của các thử nghiệm lâm sàng và kết luận rằng phân tích tổng hợp có bốn mục đích: (1) tăng cường sức mạnh thống kê bằng cách tăng cỡ mẫu, (2) giải quyết sự không chắc chắn khi các báo cáo không đồng ý, (3) cải thiện các ước tính về kích thước ảnh hưởng (effect size), và (4) trả lời các câu hỏi không được đặt ra khi bắt đầu nghiên cứu.

Bellou và cộng sự (2018) đã sử dụng phân tích tổng hợp để đánh giá các yếu tố nguy cơ của bệnh tiểu đường loại 2. Hình 10-5 minh họa cách trình bày điển hình các phát hiện từ các nghiên cứu phân tích tổng hợp.

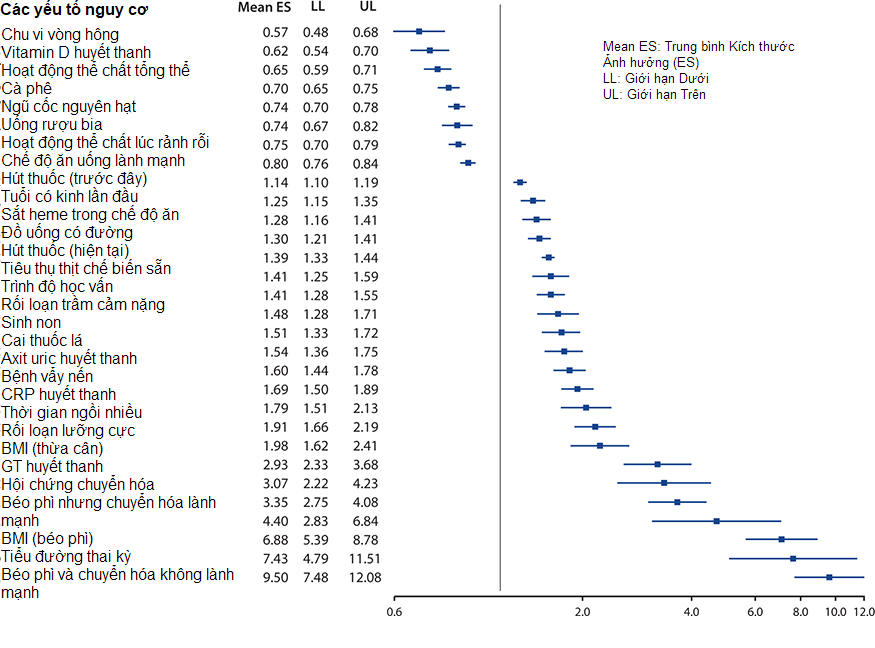
Hình 10-5. Ví dụ biểu đồ phân tích tổng hợp cho thấy dữ liệu tổng hợp về các yếu tố nguy cơ của bệnh tiểu đường loại II.

Một phân tích tổng hợp không chỉ đơn giản là cộng các giá trị trung bình hoặc tỷ lệ qua các nghiên cứu để xác định một giá trị trung bình hoặc tỷ lệ “trung bình”. Mặc dù có một số phương pháp khác nhau có thể được sử dụng để kết hợp kết quả, tất cả chúng đều sử dụng cùng một nguyên tắc là xác định một kích thước ảnh hưởng trong mỗi nghiên cứu và sau đó kết hợp các kích thước ảnh hưởng theo một cách nào đó.

CÁC PHƯƠNG PHÁP PHÂN LOẠI

Một số phương pháp đa biến có thể được sử dụng khi câu hỏi nghiên cứu liên quan đến phân loại. Khi mục tiêu là phân loại các đối tượng vào các nhóm, phân tích phân biệt (discriminant analysis), phân tích cụm (cluster analysis), và phân tích điểm xu hướng (propensity score analysis) là phù hợp.

Phân tích Phân biệt

Phân tích phân biệt tương tự như hồi quy logistic ở chỗ nó được sử dụng để dự đoán một kết cục danh nghĩa hoặc phân loại. Tuy nhiên, nó khác với hồi quy logistic ở chỗ nó giả định rằng các biến độc lập tuân theo một phân phối chuẩn đa biến.

Phân tích Nhân tố

Trong một vấn đề nghiên cứu mà phân tích nhân tố (factor analysis) là phù hợp, tất cả các biến được coi là độc lập; nói cách khác, không có mong muốn dự đoán một biến dựa trên các biến khác. Về mặt khái niệm, phân tích nhân tố hoạt động như sau: Đầu tiên, một số lượng lớn người được đo lường trên một tập hợp các mục. Bước thứ hai liên quan đến việc tính toán các tương quan. Phân tích nhân tố trả lời câu hỏi liệu một số mục có nhóm lại với nhau một cách logic hay không.

Phân tích Cụm

Một kỹ thuật thống kê tương tự về mặt khái niệm với phân tích nhân tố là phân tích cụm (cluster analysis). Sự khác biệt là phân tích cụm cố gắng tìm ra những điểm tương đồng giữa các đối tượng được đo lường thay vì giữa các phép đo đã được thực hiện.

Điểm Xu hướng

Phương pháp điểm xu hướng (propensity score) là một giải pháp thay thế cho hồi quy đa biến và phân tích hiệp phương sai. Nó cung cấp một phương pháp sáng tạo để kiểm soát toàn bộ một nhóm các biến gây nhiễu.

Cây Phân loại và Hồi quy (CART)

Phân tích cây phân loại và hồi quy (Classification and regression tree – CART) là một phương pháp tiếp cận để phân tích các cơ sở dữ liệu lớn nhằm tìm ra các mẫu và mối quan hệ có ý nghĩa giữa các biến.

NHIỀU BIẾN PHỤ THUỘC

Phân tích phương sai đa biến (MANOVA) và tương quan chính tắc (canonical correlation) tương tự nhau ở chỗ cả hai đều liên quan đến nhiều biến phụ thuộc cũng như nhiều biến độc lập.

Phân tích Phương sai Đa biến

Phân tích phương sai đa biến (Multivariate analysis of variance – MANOVA) về mặt khái niệm là một sự mở rộng đơn giản của các thiết kế ANOVA đã thảo luận trong Chương 7 sang các tình huống có hai hoặc nhiều biến phụ thuộc.

Phân tích Tương quan Chính tắc

Phân tích tương quan chính tắc (Canonical correlation analysis) cũng liên quan đến cả nhiều biến độc lập và nhiều biến phụ thuộc. Phương pháp này phù hợp khi cả biến độc lập và kết cục đều là định lượng, và câu hỏi nghiên cứu tập trung vào mối quan hệ giữa tập hợp các biến độc lập và tập hợp các biến phụ thuộc.

Ví dụ, giả sử các nhà nghiên cứu muốn kiểm tra mối quan hệ tổng thể giữa các chỉ số về kết cục sức khỏe (chức năng thể chất, sức khỏe tâm thần, nhận thức về sức khỏe, tuổi, giới tính, v.v.) được đo lường vào đầu một nghiên cứu và tập hợp các kết cục (chức năng thể chất, sức khỏe tâm thần, các mối quan hệ xã hội, các triệu chứng nghiêm trọng, v.v.) được đo lường vào cuối nghiên cứu. Phân tích tương quan chính tắc hình thành một tổ hợp tuyến tính của các biến độc lập để dự đoán không chỉ một thước đo kết cục duy nhất, mà là một tổ hợp tuyến tính của các thước đo kết cục. Hai tổ hợp tuyến tính của các biến độc lập và biến phụ thuộc, mỗi tổ hợp cho ra một con số duy nhất (hoặc chỉ số), được xác định sao cho tương quan giữa chúng là lớn nhất có thể. Tương quan giữa cặp tổ hợp tuyến tính (hoặc các con số hoặc chỉ số) được gọi là tương quan chính tắc (canonical correlation). Sau đó, cũng như trong phân tích nhân tố, một cặp tổ hợp tuyến tính thứ hai được rút ra từ phương sai còn lại sau khi ảnh hưởng của cặp thứ nhất được loại bỏ, và cặp thứ ba từ những gì còn lại, và cứ thế tiếp tục. Các hệ số chính tắc trong các tổ hợp tuyến tính được diễn giải theo cách tương tự như các hệ số hồi quy trong một phương trình hồi quy đa biến, và các tương quan chính tắc như R đa biến. Thông thường, hai hoặc ba cặp tổ hợp tuyến tính đầu tiên chiếm đủ phương sai, và chúng có thể được diễn giải để có được những hiểu biết sâu sắc về các yếu tố hoặc các chiều liên quan.

Mối quan hệ giữa tính cách và các triệu chứng trầm cảm đã được nghiên cứu trong một mẫu dựa trên cộng đồng gồm 804 cá nhân. Grucza và cộng sự (2003) đã sử dụng Bảng kiểm Khí chất và Tính cách (TCI) để đánh giá tính cách và Thang đo Trầm cảm của Trung tâm Nghiên cứu Dịch tễ học (CES-D) để đo lường các triệu chứng trầm cảm. Cả hai bảng câu hỏi này đều chứa nhiều thang đo hoặc nhân tố, và các tác giả đã sử dụng phân tích tương quan chính tắc để tìm hiểu xem các nhân tố trên TCI liên quan như thế nào đến các nhân tố trên CES-D. Họ đã phát hiện ra một số mối quan hệ và kết luận rằng mức độ nghiêm trọng và các dạng triệu chứng trầm cảm được giải thích một phần bởi các đặc điểm tính cách.

TÓM TẮT CÁC PHƯƠNG PHÁP NÂNG CAO

Các phương pháp nâng cao được trình bày trong chương này được sử dụng trong khoảng 10% đến 15% các bài báo trên các tạp chí y khoa và phẫu thuật. Thật không may cho độc giả của y văn, những phương pháp này phức tạp và không dễ hiểu, và chúng không phải lúc nào cũng được mô tả một cách đầy đủ. Cũng như các kỹ thuật thống kê phức tạp khác, các nhà điều tra nên tham khảo ý kiến của một nhà thống kê nếu một phương pháp thống kê nâng cao được lên kế hoạch. Bảng 10-2 cung cấp một hướng dẫn để lựa chọn phương pháp phù hợp, tùy thuộc vào số lượng biến độc lập và thang đo mà chúng được đo lường.

BÀI TẬP THỰC HÀNH

Bảng 10-9. Các hệ số hồi quy và giá trị kiểm định t để dự đoán số ngày nằm giường trong nghiên cứu RAND.

Các biến giải thích và các thước đo khác (X)	Hệ số (b)	Kiểm định t
Hệ số chặn	0,613	22,36
Chương trình FFS miễn phí	-0,017	-2,17
Chương trình FFS trả phí	-0,014	-2,18
Chức năng cá nhân	-0,0002	-1,35
Sức khỏe tâm thần	-0,00006	0,25
Nhận thức về sức khỏe	-0,002	-5,17
Tuổi	-0,0001	-0,54
Giới tính Nam	-0,026	-4,58
Thu nhập	-0,021	-1,65
Thời hạn ba năm	0,002	0,44
Đã khám sức khỏe	-0,003	-0,56
Số ngày nằm giường	0,105	6,15
Cỡ mẫu	1568
	0,12
Sai số chuẩn phần dư	0,01
FFS, trả phí theo dịch vụ.
Dữ liệu từ Ware JE, và cộng sự (1987).

Bảng 10-10. Các giá trị cho phương trình dự đoán.

Biến	Giá trị
Chức năng cá nhân	80
Sức khỏe tâm thần	80
Nhận thức về sức khỏe	75
Tuổi	70
Thu nhập	10 (từ một công thức được sử dụng trong nghiên cứu RAND)
Thời hạn ba nămª	Có
Đã khám sức khỏeª	Có
Số ngày nằm giường	14
ª Chỉ một biến giả với 1 = có và 0 = không.

Bảng 10-11. Kết quả hồi quy để dự đoán trầm cảm ở đợt 2.

Biến dự đoánª	b	Betaᵇ	p		Thay đổi
Điểm trầm cảm Đợt 1	0,267	0,231	0,000	0,182	0,182
Nhân khẩu-xã hội
Tuổi	-0,014	-0,024	0,538	0,187	0,005
Giới tính	0,165	0,034	0,370
Sức khỏe tâm lý
Rối loạn thần kinh, đợt 1	0,067	0,077	0,056	0,0237	0,050
Tiền sử trầm cảm	0,320	0,136	0,000
Sức khỏe thể chất
ADL, đợt 1	-0,154	-0,103	0,033	0,411	0,174
ADL, đợt 2	0,275	0,283	0,012
ADL bình phương, đợt 2	-0,013	-0,150	0,076
Số triệu chứng hiện tại, đợt 2	0,115	0,117	0,009
Số bệnh lý, đợt 2	0,309	0,226	0,000
HA, tâm thu, đợt 2	-0,010	-0,092	0,010
Thay đổi đánh giá sức khỏe toàn cầu	0,284	0,079	0,028
Thay đổi suy giảm giác quan	-0,045	-0,064	0,073
Hỗ trợ xã hội/không hoạt động
Hỗ trợ xã hội-bạn bè, đợt 2	-1,650	-0,095	0,015	0,442	0,031
Hỗ trợ xã hội-thăm viếng, đợt 2	-1,229	-0,087	0,032
Mức độ hoạt động, đợt 2	0,061	0,095	0,025
Dịch vụ (chỉ cư dân cộng đồng), đợt 2	0,207ᶜ	0,135ᶜ	0,0010	0,438ᶜ	0,015
ADL, sinh hoạt hàng ngày của người lớn; HA, huyết áp. ª Chỉ những biến được bao gồm trong mô hình cuối cùng được hiển thị. ᵇ Giá trị beta chuẩn hóa, kiểm soát tất cả các biến khác trong hồi quy, ngoại trừ việc sử dụng dịch vụ. Dựa trên cư dân cộng đồng và cơ sở. ᶜ Hồi quy chỉ giới hạn trong mẫu cộng đồng; các hệ số cho các biến khác chỉ thay đổi rất nhỏ so với những gì thu được với hồi quy trên mẫu đầy đủ. Sửa đổi với sự cho phép từ Henderson AS, và cộng sự (1997).

Bảng 10-12. Tóm tắt các trường hợp.ª

Chiều cao cuối cùng SDS	Tuổi	Liều	Chiều cao của Cha	Chiều cao của Mẹ	Chiều cao SDS Tuổi theo thời gian	Chiều cao SDS Tuổi xương
-2,18	6,652	20,00	-2,14	-2,20	-3,07	-1,75
-2,15	10,383	16,00	-2,78	-0,15	-2,20	-2,43
-1,65	10,565	16,00	-1,91	-1,87	-2,62	-0,90
-1,18	10,104	15,00	0,84	-1,63	-2,43	-2,06
-1,31	11,145	14,00	-1,80	-0,70	-1,92	-1,49
-1,35	9,682	14,00	0,09	0,38	-1,38	-0,54
-1,18	9,863	16,00	-0,26	-1,70	-2,08	-1,32
-2,51	9,463	15,00	-3,62	-0,75	-2,36	-0,45
-1,61	7,704	19,00	-2,11	-1,25	-1,98	1,23
-2,15	5,858	25,00	1,31	0,23	-2,43	-1,95
0,80	5,153	22,00	-0,14	-1,83	-2,36	-0,39
-0,20	6,986	21,00	-0,14	-1,83	-2,09	-0,98
0,20	8,967	17,00	-0,14	-1,83	-1,38	-0,19
-0,71	6,970	21,00	0,50	1,63	-1,09	0,49
-1,71	6,515	13,00	0,84	-0,10	-1,98	-0,18
-2,32	7,548	21,00	-2,89	-0,20	-3,30	-2,25
Tổng N	16	16	16	16	16	16
SDS, điểm độ lệch chuẩn. ª Giới hạn trong 100 trường hợp đầu tiên. Dữ liệu từ Hindmarsh PC, Brook CG (1996).

Bảng 10-13. Kết quả từ hồi quy đa biến từng bước để dự đoán chiều cao cuối cùng theo điểm độ lệch chuẩn.

Model		Hệ số chưa chuẩn hóa		Hệ số chuẩn hóa
		B	SE	β	t	Ý nghĩa
1	(Hằng số)	-1,055	0,248		-4,261	0,001
	Chiều cao của cha	0,302	0,142	0,494	2,126	0,052
2	(Hằng số)	-1,335	0,284		-4,705	0,000
	Chiều cao của cha	0,337	0,135	0,552	2,503	0,026
	Chiều cao của mẹ	-0,343	0,200	-0,378	-1,715	0,110
3	(Hằng số)	0,205	0,734		0,280	0,785
	Chiều cao của cha	0,211	0,131	0,345	1,612	0,133
	Chiều cao của mẹ	-0,478	0,185	-0,527	-2,581	0,024
	Chiều cao SDS tuổi theo thời gian	0,820	0,368	0,505	2,230	0,046
4	(Hằng số)	-1,110	0,927		-1,198	0,256
	Chiều cao của cha	0,128	0,124	0,210	1,035	0,323
	Chiều cao của mẹ	-0,559	0,170	-0,617	-3,284	0,007
	Chiều cao SDS tuổi theo thời gian	1,132	0,363	0,697	3,116	0,010
	Liều	0,104	0,052	0,385	2,009	0,070
5	(Hằng số)	-1,138	0,929		-1,225	0,244
	Chiều cao của mẹ	-0,575	0,170	-0,634	-3,381	0,005
	Chiều cao SDS tuổi theo thời gian	1,325	0,313	0,816	4,229	0,001
	Liều	0,121	0,049	0,451	2,487	0,029
SE, sai số chuẩn; SDS, điểm độ lệch chuẩn. Biến phụ thuộc: chiều cao cuối cùng SDS. Lưu ý: Vì cỡ mẫu nhỏ, chúng tôi đặt xác suất để các biến nhập vào phương trình hồi quy là 0,15 và để các biến bị loại bỏ là 0,20. Dữ liệu từ Hindmarsh PC, Brook CG (1996).

Bảng Chú giải Thuật ngữ Thống kê Anh – Việt (Chương 10)

STT	Tên thuật ngữ tiếng Anh	Phiên âm	Nghĩa tiếng Việt
1	Multiple Variables	/ˈmʌltɪpəl ˈveriəbəlz/	Nhiều Biến số
2	Statistical Methods	/stəˈtɪstɪkəl ˈmeθədz/	Các Phương pháp Thống kê
3	Research Question	/rɪˈsɜːrtʃ ˈkwestʃən/	Câu hỏi Nghiên cứu
4	Scales of measurement	/skeɪlz əv ˈmeʒərmənt/	Các thang đo lường
5	Multiple Regression Analysis	/ˈmʌltɪpəl rɪˈɡreʃən əˈnæləsɪs/	Phân tích Hồi quy Đa biến
6	Independent Variable	/ˌɪndɪˈpendənt ˈveriəbəl/	Biến độc lập
7	Dependent Variable	/dɪˈpendənt ˈveriəbəl/	Biến phụ thuộc
8	Multivariate	/ˌmʌltiˈveriət/	Đa biến
9	Confounding Variables	/kənˈfaʊndɪŋ ˈveriəbəlz/	Các biến gây nhiễu
10	Multiple Regression Coefficients	/ˈmʌltɪpəl rɪˈɡreʃən ˌkoʊɪˈfɪʃənts/	Các hệ số Hồi quy Đa biến
11	Dummy Coding	/ˈdʌmi ˈkoʊdɪŋ/	Mã hóa giả
12	Indicator Coding	/ˈɪndɪkeɪtər ˈkoʊdɪŋ/	Mã hóa chỉ báo
13	Linear Relationship	/ˈlɪniər rɪˈleɪʃənʃɪp/	Mối quan hệ Tuyến tính
14	Multiple R	/ˈmʌltɪpəl ɑːr/	R Đa biến
15	Variance	/ˈveriəns/	Phương sai
16	Model	/ˈmɒdəl/	Mô hình
17	Polynomial Regression	/ˌpɒlɪˈnoʊmiəl rɪˈɡreʃən/	Hồi quy Đa thức
18	Curvilinear	/ˌkɜːrvɪˈlɪniər/	Cong (Phi tuyến tính)
19	Cross-validation	/krɒs ˌvælɪˈdeɪʃən/	Kiểm định chéo
20	Rule of thumb	/ruːl əv θʌm/	Quy tắc kinh nghiệm
21	Analysis of Covariance (ANCOVA)	/əˈnæləsɪs əv ˌkoʊˈveriəns/	Phân tích Hiệp phương sai
22	Logistic Regression	/ləˈdʒɪstɪk rɪˈɡreʃən/	Hồi quy Logistic
23	Nominal Outcome	/ˈnɒmɪnəl ˈaʊtkʌm/	Kết cục danh nghĩa
24	Odds Ratios	/ɒdz ˈreɪʃiəʊz/	Tỷ số chênh
25	Cox Model	/kɒks ˈmɒdəl/	Mô hình Cox
26	Time-dependent Outcomes	/taɪm dɪˈpendənt ˈaʊtkʌmz/	Các kết cục phụ thuộc thời gian
27	Censored Observations	/ˈsensərd ˌɒbzərˈveɪʃənz/	Các quan sát bị kiểm duyệt
28	Proportional Hazard Model	/prəˈpɔːrʃənəl ˈhæzərd ˈmɒdəl/	Mô hình Nguy cơ Tỷ lệ thuận
29	Meta-analysis	/ˈmetə əˈnæləsɪs/	Phân tích tổng hợp
30	Quantitative	/ˈkwɒntɪtətɪv/	Định lượng
31	Effect Size	/ɪˈfekt saɪz/	Kích thước ảnh hưởng
32	Magnitude of differences	/ˈmæɡnɪtjuːd əv ˈdɪfrənsɪz/	Độ lớn của sự khác biệt
33	Sample Sizes	/ˈsæmpəl saɪzɪz/	Cỡ mẫu
34	Cochrane Collection	/ˈkɒkrən kəˈlekʃən/	Bộ sưu tập Cochrane
35	Classify subjects	/ˈklæsɪfaɪ ˈsʌbdʒekts/	Phân loại đối tượng
36	Multivariate Analysis of Variance (MANOVA)	/ˌmʌltiˈveriət əˈnæləsɪs əv ˈveriəns/	Phân tích Phương sai Đa biến
37	Conceptual Framework	/kənˈsepʧuəl ˈfreɪmwɜːrk/	Khung khái niệm
38	t-test	/ˈtiː test/	Phép kiểm t
39	Numerical Variable	/njuːˈmerɪkəl ˈveriəbəl/	Biến định lượng
40	Nominal Variable	/ˈnɒmɪnəl ˈveriəbəl/	Biến danh nghĩa
41	Chi-square test	/kaɪ skwer test/	Phép kiểm Chi-bình phương
42	Regression Analysis	/rɪˈɡreʃən əˈnæləsɪs/	Phân tích Hồi quy
43	Group Membership	/ɡruːp ˈmembərʃɪp/	Tư cách thành viên nhóm
44	One-way ANOVA	/wʌn weɪ əˈnoʊvə/	ANOVA một chiều
45	Two-way ANOVA	/tuː weɪ əˈnoʊvə/	ANOVA hai chiều
46	Ordinal Variables	/ˈɔːrdɪnəl ˈveriəbəlz/	Các biến thứ tự
47	Explanatory Variables	/ɪkˈsplænətɔːri ˈveriəbəlz/	Các biến giải thích
48	Response Variable	/rɪˈspɒns ˈveriəbəl/	Biến phản hồi (Biến phụ thuộc)
49	Log-linear analysis	/lɒɡ ˈlɪniər əˈnæləsɪs/	Phân tích Log-linear
50	Discriminant analysis	/dɪˈskrɪmɪnənt əˈnæləsɪs/	Phân tích phân biệt
51	Cluster analysis	/ˈklʌstər əˈnæləsɪs/	Phân tích cụm
52	Propensity scores	/prəˈpensəti skɔːrz/	Điểm xu hướng
53	CART (Classification and Regression Tree)	/kɑːrt/	Cây Phân loại và Hồi quy
54	Factor analysis	/ˈfæktər əˈnæləsɪs/	Phân tích nhân tố
55	GEE (Generalized Estimating Equations)	/dʒiː iː iː/	Phương trình Ước tính Tổng quát
56	Multivariate normality	/ˌmʌltiˈveriət nɔːrˈmæləti/	Tính chuẩn đa biến
57	Simple Linear Regression	/ˈsɪmpəl ˈlɪniər rɪˈɡreʃən/	Hồi quy Tuyến tính Đơn
58	Intercept	/ˈɪntərsept/	Hệ số chặn
59	Regression Coefficient	/rɪˈɡreʃən ˌkoʊɪˈfɪʃənt/	Hệ số hồi quy
60	Sample estimates	/ˈsæmpəl ˈestɪməts/	Các ước tính mẫu
61	Population parameters	/ˌpɒpjuˈleɪʃən pəˈræmɪtərz/	Các tham số quần thể
62	Linear Combination	/ˈlɪniər ˌkɒmbɪˈneɪʃən/	Tổ hợp tuyến tính
63	Weighted average	/ˈweɪtɪd ˈævərɪdʒ/	Trung bình có trọng số
64	Collinear	/kəˈlɪniər/	Cộng tuyến
65	Multicollinearity	/ˌmʌltikoʊˌlɪniˈærəti/	Đa cộng tuyến
66	Ridge Regression	/rɪdʒ rɪˈɡreʃən/	Hồi quy Ridge
67	Principal Components Regression	/ˈprɪnsəpəl kəmˈpoʊnənts rɪˈɡreʃən/	Hồi quy Thành phần Chính
68	Binary variable	/ˈbaɪnəri ˈveriəbəl/	Biến nhị phân
69	Unstandardized coefficients	/ʌnˈstændərdaɪzd ˌkoʊɪˈfɪʃənts/	Các hệ số chưa chuẩn hóa
70	Standardized Regression Coefficients	/ˈstændərdaɪzd rɪˈɡreʃən ˌkoʊɪˈfɪʃənts/	Các hệ số Hồi quy Chuẩn hóa
71	Beta coefficients	/ˈbeɪtə ˌkoʊɪˈfɪʃənts/	Các hệ số beta
72	Moderator variable	/ˈmɒdəreɪtər ˈveriəbəl/	Biến điều tiết
73	Coefficient of multiple determination	/ˌkoʊɪˈfɪʃənt əv ˈmʌltɪpəl dɪˌtɜːrmɪˈneɪʃən/	Hệ số xác định đa biến
74	R-squared (R²)	/ɑːr skwerd/	R-bình phương (R²)
75	F distribution	/ef ˌdɪstrɪˈbjuːʃən/	Phân phối F
76	Model building	/ˈmɒdəl ˈbɪldɪŋ/	Xây dựng mô hình
77	“Enter” method	/ˈentər ˈmeθəd/	Phương pháp “Nhập” (đưa tất cả biến vào cùng lúc)
78	Forward selection	/ˈfɔːrwərd sɪˈlekʃən/	Lựa chọn tiến
79	Backward elimination	/ˈbækwərd ɪˌlɪmɪˈneɪʃən/	Loại bỏ lùi
80	Stepwise regression	/ˈstepwaɪz rɪˈɡreʃən/	Hồi quy từng bước
81	Parsimonious equation	/ˌpɑːrsɪˈmoʊniəs ɪˈkweɪʒən/	Phương trình tinh gọn (tiết kiệm biến)
82	Hierarchical regression	/ˌhaɪəˈrɑːrkɪkəl rɪˈɡreʃən/	Hồi quy phân cấp
83	Quadratic relationship	/kwɒˈdrætɪk rɪˈleɪʃənʃɪp/	Mối quan hệ bậc hai
84	Cubic term	/ˈkjuːbɪk tɜːrm/	Số hạng bậc ba
85	Curve fitting	/kɜːrv ˈfɪtɪŋ/	Khớp đường cong
86	Missing Observations	/ˈmɪsɪŋ ˌɒbzərˈveɪʃənz/	Các quan sát bị thiếu
87	Prospectively	/prəˈspektɪvli/	(Thu thập) tiến cứu
88	Case-control study	/keɪs kənˈtroʊl ˈstʌdi/	Nghiên cứu bệnh-chứng
89	Imputing	/ɪmˈpjuːtɪŋ/	Gán giá trị (thay thế dữ liệu thiếu)
90	Holdout sample	/ˈhoʊldaʊt ˈsæmpəl/	Mẫu giữ lại (để kiểm định)
91	Jackknife method	/ˈdʒæknaɪf ˈmeθəd/	Phương pháp Jackknife
92	Bootstrap method	/ˈbuːtstræp ˈmeθəd/	Phương pháp Bootstrap
93	Resampling methods	/riːˈsæmplɪŋ ˈmeθədz/	Các phương pháp lấy mẫu lại
94	Shrinkage	/ˈʃrɪŋkɪdʒ/	Sự co lại (của R²)
95	Adjusted R-squared	/əˈdʒʌstɪd ɑːr skwerd/	R-bình phương điều chỉnh
96	Power program	/ˈpaʊər ˈproʊɡræm/	Chương trình tính công suất
97	Power curve	/ˈpaʊər kɜːrv/	Đường cong công suất
98	Covariate	/ˌkoʊˈveriət/	Hiệp biến
99	Adjusted mean	/əˈdʒʌstɪd miːn/	Trung bình điều chỉnh
100	Unadjusted mean	/ˌʌnəˈdʒʌstɪd miːn/	Trung bình chưa điều chỉnh
101	Regression slopes	/rɪˈɡreʃən sloʊps/	Các độ dốc hồi quy
102	Coincident (lines)	/koʊˈɪnsɪdənt/	(Các đường) trùng nhau
103	Interaction	/ˌɪntərˈækʃən/	Tương tác
104	Clustered observations	/ˈklʌstərd ˌɒbzərˈveɪʃənz/	Các quan sát được phân cụm
105	Hierarchical data	/ˌhaɪəˈrɑːrkɪkəl ˈdeɪtə/	Dữ liệu phân cấp
106	Nested (data)	/ˈnestɪd/	(Dữ liệu) lồng nhau
107	Unit of analysis	/ˈjuːnɪt əv əˈnæləsɪs/	Đơn vị phân tích
108	Multilevel modeling	/ˌmʌltiˈlevəl ˈmɒdəlɪŋ/	Mô hình hóa đa cấp
109	Binary outcome	/ˈbaɪnəri ˈaʊtkʌm/	Kết cục nhị phân
110	Dichotomous outcome	/daɪˈkɒtəməs ˈaʊtkʌm/	Kết cục lưỡng phân
111	Exponential function	/ˌekspəˈnenʃəl ˈfʌŋkʃən/	Hàm số mũ
112	Goodness of fit test	/ˈɡʊdnəs əv fɪt test/	Phép kiểm độ phù hợp
113	Classification table	/ˌklæsɪfɪˈkeɪʃən ˈteɪbəl/	Bảng phân loại
114	Kappa statistic	/ˈkæpə stəˈtɪstɪk/	Thống kê Kappa
115	Nonparametric correlations	/ˌnɒnpærəˈmetrɪk ˌkɒrəˈleɪʃənz/	Các tương quan phi tham số
116	Lambda correlation	/ˈlæmdə ˌkɒrəˈleɪʃən/	Tương quan Lambda
117	Tau correlation	/taʊ ˌkɒrəˈleɪʃən/	Tương quan Tau
118	Contingency table	/kənˈtɪndʒənsi ˈteɪbəl/	Bảng ngẫu nhiên
119	Multidimensional contingency tables	/ˌmʌltidaɪˈmenʃənəl kənˈtɪndʒənsi ˈteɪbəlz/	Các bảng ngẫu nhiên đa chiều
120	Covariates	/ˌkoʊˈveriəts/	Các hiệp biến
121	Relative risk	/ˈrelətɪv rɪsk/	Nguy cơ tương đối
122	Baseline hazard	/ˈbeɪslaɪn ˈhæzərd/	Nguy cơ cơ bản
123	Multiplicative effect	/ˌmʌltɪˈplɪkətɪv ɪˈfekt/	Hiệu ứng nhân
124	Proportional effect	/prəˈpɔːrʃənəl ɪˈfekt/	Hiệu ứng tỷ lệ thuận
125	Mortality rate ratios (MRR)	/mɔːrˈtæləti reɪt ˈreɪʃiəʊz/	Tỷ số suất tử vong
126	Statistical power	/stəˈtɪstɪkəl ˈpaʊər/	Sức mạnh thống kê (Công suất)
127	Mendelian randomization (MR)	/menˈdiːliən ˌrændəmaɪˈzeɪʃən/	Phân ngẫu nhiên Mendel
128	Risk estimates	/rɪsk ˈestɪməts/	Các ước tính nguy cơ
129	Summary odds ratios	/ˈsʌməri ɒdz ˈreɪʃiəʊz/	Các tỷ số chênh tóm tắt
130	Pooled p-value	/puːld piː ˈvæljuː/	Giá trị p gộp
131	Publication bias	/ˌpʌblɪˈkeɪʃən ˈbaɪəs/	Sai lệch công bố
132	Heterogeneity	/ˌhetərəʊdʒəˈniːəti/	Tính không đồng nhất
133	Systematic Reviews	/ˌsɪstəˈmætɪk rɪˈvjuːz/	Các tổng quan hệ thống
134	Discriminant functions	/dɪˈskrɪmɪnənt ˈfʌŋkʃənz/	Các hàm phân biệt
135	Wilks’ lambda	/wɪlks ˈlæmdə/	Lambda của Wilks
136	Factors	/ˈfæktərz/	Các nhân tố
137	Taxonomic scheme	/ˌtæksəˈnɒmɪk skiːm/	Sơ đồ phân loại
138	Q-type factor analysis	/kjuː taɪp ˈfæktər əˈnæləsɪs/	Phân tích nhân tố loại Q
139	Cut points	/kʌt pɔɪnts/	Các điểm cắt
140	Univariate ANOVA	/ˌjuːnɪˈveriət əˈnoʊvə/	ANOVA đơn biến
141	Canonical Correlation Analysis	/kəˈnɒnɪkəl ˌkɒrəˈleɪʃən əˈnæləsɪs/	Phân tích Tương quan Chính tắc
142	Canonical correlation	/kəˈnɒnɪkəl ˌkɒrəˈleɪʃən/	Tương quan chính tắc
143	Canonical coefficients	/kəˈnɒnɪkəl ˌkoʊɪˈfɪʃənts/	Các hệ số chính tắc
144	Ponderal index	/ˈpɒndərəl ˈɪndeks/	Chỉ số Ponderal (chỉ số khối lượng cơ thể)
145	Anthropometric variables	/ˌænθrəpəˈmetrɪk ˈveriəbəlz/	Các biến nhân trắc học
146	Fee-for-service (FFS)	/fiː fər ˈsɜːrvɪs/	Trả phí theo dịch vụ
147	Health maintenance organizations (HMO)	/helθ ˈmeɪntənəns ˌɔːrɡənaɪˈzeɪʃənz/	Các tổ chức bảo trì sức khỏe
148	Residual standard error	/rɪˈzɪdjuəl ˈstændərd ˈerər/	Sai số chuẩn phần dư
149	Cognitive performance	/ˈkɒɡnɪtɪv pərˈfɔːrməns/	Hiệu suất nhận thức
150	Standard deviation scores (SDS)	/ˈstændərd ˌdiːviˈeɪʃən skɔːrz/	Các điểm độ lệch chuẩn