Thống kê Sinh học Cơ bản và Lâm sàng, Ấn bản thứ 5. Chương 4: Xác suất & Các chủ đề liên quan để Suy luận về Dữ liệu

Thống kê Sinh học Cơ bản và Lâm sàng, Ấn bản thứ 5 – Basic & Clinical Biostatistics, 5e
Tác giả: Susan White – Nhà xuất bản McGraw-Hill Medical – Biên dịch: Ths.Bs. Lê Đình Sáng

Chương 4: Xác suất & Các chủ đề liên quan để Suy luận về Dữ liệu

Probability & Related Topics for Making Inferences About Data

CÁC KHÁI NIỆM CHÍNH

Xác suất là một khái niệm quan trọng trong thống kê. Cả xác suất khách quan và chủ quan đều được sử dụng trong lĩnh vực y học.
Các định nghĩa cơ bản bao gồm khái niệm về một biến cố hoặc kết quả. Một số quy tắc thiết yếu cho chúng ta biết cách kết hợp các xác suất của các biến cố.
Định lý Bayes liên quan đến khái niệm xác suất có điều kiện—xác suất của một kết quả phụ thuộc vào một kết quả trước đó. Định lý Bayes là một phần của quá trình suy luận khi diễn giải các quy trình chẩn đoán.
Các quần thể hiếm khi được nghiên cứu; thay vào đó, các nhà nghiên cứu nghiên cứu các mẫu.
Một số phương pháp lấy mẫu được sử dụng trong nghiên cứu y học; một vấn đề quan trọng là bất kỳ phương pháp nào cũng phải là ngẫu nhiên.
Khi các nhà nghiên cứu chọn các mẫu ngẫu nhiên và sau đó thực hiện các phép đo, kết quả là một biến ngẫu nhiên. Quá trình này làm cho các kiểm định và suy luận thống kê trở nên khả thi.
Phân phối nhị thức được sử dụng để xác định xác suất của các biến cố có/không—số lần một kết quả nhất định xảy ra trong một số lần thử nhất định.
Phân phối Poisson được sử dụng để xác định xác suất của các biến cố hiếm gặp.
Phân phối chuẩn được sử dụng để tìm xác suất một kết quả xảy ra khi các quan sát có phân phối hình chuông. Nó được sử dụng trong nhiều thủ tục thống kê.
Nếu nhiều mẫu ngẫu nhiên được rút ra từ một quần thể, một thống kê, chẳng hạn như giá trị trung bình, sẽ tuân theo một phân phối gọi là phân phối lấy mẫu.
Định lý giới hạn trung tâm cho chúng ta biết rằng các giá trị trung bình của các quan sát, bất kể chúng được phân phối như thế nào, bắt đầu tuân theo phân phối chuẩn khi cỡ mẫu tăng lên. Đây là một trong những lý do tại sao phân phối chuẩn rất quan trọng trong thống kê.
Điều quan trọng là phải biết sự khác biệt giữa độ lệch chuẩn, mô tả sự phân tán của các quan sát riêng lẻ, và sai số chuẩn của trung bình, mô tả sự phân tán của các quan sát trung bình.
Một trong những mục đích của thống kê là sử dụng một mẫu để ước tính một điều gì đó về quần thể. Các ước tính tạo thành cơ sở của các kiểm định thống kê.
Các khoảng tin cậy có thể được hình thành xung quanh một ước tính để cho chúng ta biết ước tính đó sẽ thay đổi bao nhiêu trong các mẫu lặp lại.

CÁC VẤN ĐỀ TÌNH HUỐNG

Vấn đề Tình huống 1

Tổ chức Y tế Thế giới (WHO) thu thập tỷ lệ mắc cúm trên toàn thế giới. CDC thu thập số liệu thống kê cho Hoa Kỳ và các vùng lãnh thổ. Việc thu thập dữ liệu được hoàn thành hàng tuần thông qua các phòng thí nghiệm hợp tác của NREVSS. Dữ liệu cho mùa cúm 2017-2018 được sử dụng làm Vấn đề Tình huống để minh họa các khái niệm về xác suất và được hiển thị trong Bảng 4-1.

Vấn đề Tình huống 2

Một ngân hàng máu địa phương được yêu cầu cung cấp thông tin về sự phân bố các nhóm máu giữa nam và nữ. Thông tin này hữu ích trong việc minh họa một số nguyên tắc cơ bản trong lý thuyết xác suất. Kết quả được đưa ra trong phần “Các Định nghĩa và Quy tắc Cơ bản của Xác suất.”

Vấn đề Tình huống 3

Tại Hoa Kỳ, ung thư tuyến tiền liệt là nguyên nhân gây tử vong đứng hàng thứ hai trong số những người đàn ông chết vì khối u ác tính, chiếm 12.3% số ca tử vong do ung thư. Những người đàn ông được điều trị phẫu thuật bằng phương pháp cắt bỏ tuyến tiền liệt triệt để thường cũng được điều trị bằng xạ trị cứu vớt. Shipley và các đồng nghiệp (2017) đã điều tra tiện ích của việc bổ sung liệu pháp kháng androgen cùng với xạ trị có thể giúp kéo dài thời gian sống còn hay không.

Vấn đề Tình huống 4

Nghiên cứu Phẫu thuật Động mạch Vành (CASS) là một nghiên cứu kinh điển vào năm 1983; đó là một thử nghiệm hợp tác đa trung tâm, tiến cứu, ngẫu nhiên về liệu pháp nội khoa và phẫu thuật ở các phân nhóm bệnh nhân mắc bệnh tim thiếu máu cục bộ ổn định. Nghiên cứu kinh điển này đã xác định rằng tỷ lệ sống còn 10 năm trong nhóm bệnh nhân này là tốt như nhau ở nhóm được điều trị nội khoa và nhóm được điều trị phẫu thuật (tái thông mạch vành) (Alderman và cộng sự 1990). Một phần thứ hai của nghiên cứu đã so sánh tác động của điều trị nội khoa và phẫu thuật đối với chất lượng cuộc sống.

MỤC ĐÍCH CỦA CHƯƠNG

Chương trước đã trình bày các phương pháp tóm tắt thông tin từ các nghiên cứu: đồ thị, biểu đồ và các thống kê tóm tắt. Tuy nhiên, một lý do chính để thực hiện nghiên cứu lâm sàng là để khái quát hóa các phát hiện từ tập hợp các quan sát trên một nhóm đối tượng cho những người khác tương tự như các đối tượng đó. Shipley và các đồng nghiệp (2017) đã kết luận rằng liệu pháp kháng androgen với bicalutamide hàng ngày kết hợp với xạ trị cứu vớt đã mang lại thời gian sống còn toàn bộ dài hơn so với xạ trị và giả dược. Kết luận này dựa trên nghiên cứu và theo dõi của họ trong thời gian trung bình là 13 năm trên 760 người đàn ông. Việc nghiên cứu tất cả các bệnh nhân trên thế giới có khối u T2 và T3 không có sự tham gia của hạch bạch huyết là không thể và không mong muốn; do đó, các nhà điều tra đã đưa ra các suy luận (Inferences) cho một quần thể bệnh nhân lớn hơn dựa trên nghiên cứu của họ về một mẫu bệnh nhân. Họ không thể chắc chắn rằng những người đàn ông có một khối u cụ thể hoặc một liệu trình xạ trị cụ thể sẽ phản ứng với điều trị như người đàn ông trung bình trong nghiên cứu này, nhưng họ có thể sử dụng dữ liệu để tìm ra xác suất của một phản ứng tích cực.

Các khái niệm trong chương này sẽ cho phép bạn hiểu các nhà điều tra có ý gì khi họ đưa ra những tuyên bố như sau:

Sự khác biệt giữa nhóm điều trị và nhóm đối chứng đã được kiểm định bằng cách sử dụng kiểm định t và được phát hiện là lớn hơn không một cách có ý nghĩa.
Giá trị a là 0.01 đã được sử dụng cho tất cả các kiểm định thống kê.
Cỡ mẫu được xác định để có 90% lực thống kê nhằm phát hiện sự khác biệt 30% giữa nhóm điều trị và nhóm đối chứng.

Nhiều khái niệm nền tảng của suy luận thống kê không dễ dàng tiếp thu trong lần đọc đầu tiên. Chương này nên được xem lại sau khi hoàn thành các Chương 5 đến 9 để củng cố sự hiểu biết về các khái niệm. Sẽ dễ dàng hơn để hiểu các ý tưởng cơ bản của suy luận bằng cách sử dụng phương pháp tiếp cận này.

Ý NGHĨA CỦA THUẬT NGỮ “XÁC SUẤT”

Giả sử một thí nghiệm có thể được lặp lại nhiều lần, với mỗi lần lặp lại được gọi là một phép thử (trial) và giả sử một hoặc nhiều kết quả (outcomes) có thể xảy ra từ mỗi phép thử. Khi đó, xác suất (probability) của một kết quả nhất định là số lần kết quả đó xảy ra chia cho tổng số phép thử. Nếu một kết quả chắc chắn xảy ra, nó có xác suất là 1; nếu một kết quả không thể xảy ra, xác suất của nó là 0.

Một ước tính về xác suất có thể được xác định theo kinh nghiệm, hoặc nó có thể dựa trên một mô hình lý thuyết. Chúng ta biết rằng xác suất tung một đồng xu cân đối và nhận được mặt ngửa là 0.50, hay 50%. Nếu một đồng xu được tung mười lần, tất nhiên, không có gì đảm bảo rằng sẽ quan sát được chính xác năm mặt ngửa; tỷ lệ mặt ngửa có thể dao động từ 0 đến 1, mặc dù trong hầu hết các trường hợp chúng ta mong đợi nó gần 0.50 hơn là 0 hoặc 1. Nếu đồng xu được tung 100 lần, cơ hội tỷ lệ mặt ngửa sẽ gần 0.50 còn cao hơn, và với 1.000 lần tung, cơ hội còn cao hơn nữa. Khi số lần tung trở nên lớn hơn, tỷ lệ các lần tung đồng xu có kết quả là mặt ngửa tiến gần đến 0.50; do đó, xác suất của mặt ngửa trong bất kỳ lần tung nào là 0.50.

Định nghĩa này về xác suất đôi khi được gọi là xác suất khách quan (objective probability), trái ngược với xác suất chủ quan (subjective probability), phản ánh ý kiến, linh cảm, hoặc phỏng đoán tốt nhất của một người về việc một kết quả sẽ xảy ra. Xác suất chủ quan rất quan trọng trong y học vì chúng hình thành cơ sở cho ý kiến của bác sĩ về việc một bệnh nhân có mắc một bệnh cụ thể hay không. Trong Chương 12, chúng ta thảo luận về cách ước tính này, dựa trên thông tin thu được từ bệnh sử và khám thực thể, thay đổi như thế nào theo kết quả của các quy trình chẩn đoán.

CÁC ĐỊNH NGHĨA VÀ QUY TẮC CƠ BẢN CỦA XÁC SUẤT

Các khái niệm xác suất rất hữu ích để hiểu và diễn giải dữ liệu được trình bày trong các bảng và đồ thị trong các bài báo đã xuất bản. Ngoài ra, khái niệm xác suất cho phép chúng ta đưa ra các tuyên bố về mức độ tin cậy của chúng ta đối với các ước tính như giá trị trung bình, tỷ lệ, hoặc nguy cơ tương đối (được giới thiệu trong chương trước). Hiểu về xác suất là điều cần thiết để hiểu ý nghĩa của các giá trị p được đưa ra trong các bài báo khoa học.

Chúng ta sử dụng hai ví dụ để minh họa một số định nghĩa và quy tắc để xác định xác suất: Vấn đề Tình huống 1 về bệnh cúm (Bảng 4-1) và thông tin được đưa ra trong Bảng 4-2 về giới tính và nhóm máu. Tất cả các minh họa về xác suất đều giả định rằng quan sát đã được chọn ngẫu nhiên từ một quần thể các quan sát.

Bảng 4-1. Tóm tắt loại virus cúm theo nhóm tuổi cho mùa 2017-2018.

Nhóm Tuổi	Virus Cúm A		Virus Cúm B		Tổng
	Số lượng	% theo Cột	Số lượng	% theo Cột
0-4 tuổi	2,989	9%	952	7%	3,941
5-24 tuổi	7,489	22%	4,296	31%	11,785
25-64 tuổi	11,403	33%	4,618	33%	16,021
65+ tuổi	12,448	36%	4,096	29%	16,544
Tổng	34,329	100%	13,962	100%	48,291

Sao chép với sự cho phép của Trung tâm Kiểm soát và Phòng ngừa Dịch bệnh.

Bảng 4-2. Phân bố nhóm máu theo giới tính.

Nhóm Máu	Xác suất
	Nam	Nữ	Tổng
O	0.21	0.21	0.42
A	0.215	0.215	0.43
B	0.055	0.055	0.11
AB	0.02	0.02	0.04
Tổng	0.50	0.50	1.00

Trong xác suất, một thí nghiệm (experiment) được định nghĩa là bất kỳ quá trình thu thập dữ liệu có kế hoạch nào. Đối với Vấn đề Tình huống 1, thí nghiệm là quá trình xác định loại virus ở bệnh nhân cúm. Một thí nghiệm bao gồm một số phép thử (trials) độc lập trong cùng điều kiện; trong ví dụ này, một phép thử bao gồm việc xác định loại virus cho một người. Mỗi phép thử có thể dẫn đến một trong hai kết quả: A hoặc B.

Xác suất của một kết quả cụ thể, giả sử là kết quả A, được viết là

. Ví dụ, trong Bảng 4-1, nếu kết quả A là Virus A, xác suất một người được chọn ngẫu nhiên từ nghiên cứu mắc Cúm loại A là:

Trong Vấn đề Tình huống 2, xác suất của các kết quả khác nhau đã được tính toán sẵn. Các kết quả của mỗi phép thử để xác định nhóm máu là O, A, B, và AB. Từ Bảng 4-2, xác suất một người được chọn ngẫu nhiên có nhóm máu A là:

$P(\text{nhóm máu A}) = 0.43$

Dữ liệu nhóm máu minh họa hai đặc điểm quan trọng của xác suất:

Xác suất của mỗi kết quả (nhóm máu) lớn hơn hoặc bằng 0.
Tổng xác suất của các kết quả khác nhau là 1.

Biến cố (Hay Sự kiện) (Events) có thể được định nghĩa là một kết quả duy nhất hoặc một tập hợp các kết quả. Đôi khi, chúng ta muốn biết xác suất một biến cố sẽ không xảy ra; một biến cố đối lập với biến cố quan tâm được gọi là biến cố bù (complementary event). Xác suất của biến cố bù có thể được tìm thấy bằng 1 trừ đi xác suất của chính biến cố đó.

Biến cố Xung khắc và Quy tắc Cộng

Hai hay nhiều biến cố là xung khắc (mutually exclusive) nếu sự xuất hiện của một biến cố loại trừ sự xuất hiện của các biến cố khác. Ví dụ, một người không thể vừa có nhóm máu O vừa có nhóm máu A.

Xác suất để hai biến cố xung khắc xảy ra là xác suất để một trong hai biến cố đó xảy ra. Xác suất này được tìm thấy bằng cách cộng xác suất của hai biến cố, được gọi là quy tắc cộng (addition rule) cho xác suất. Ví dụ, xác suất một người được chọn ngẫu nhiên có nhóm máu O hoặc nhóm máu A là:

Biến cố Độc lập và Quy tắc Nhân

Hai biến cố khác nhau là biến cố độc lập (independent events) nếu kết quả của một biến cố không ảnh hưởng đến kết quả của biến cố thứ hai. Ví dụ, giới tính và nhóm máu là các biến cố độc lập. Xác suất của hai biến cố độc lập là xác suất cả hai biến cố cùng xảy ra và được tìm thấy bằng cách nhân xác suất của hai biến cố, được gọi là quy tắc nhân (multiplication rule) cho xác suất. Xác suất là nam và có nhóm máu O là:

Xác suất là nam, 0.50, và xác suất có nhóm máu O, 0.42, đều được gọi là xác suất biên (marginal probabilities). Xác suất là nam và có nhóm máu O, 0.21, được gọi là xác suất đồng thời (joint probability).

Biến cố Không độc lập và Quy tắc Nhân Mở rộng

Khi hai biến cố không độc lập, sự xuất hiện của một biến cố phụ thuộc vào việc biến cố kia có xảy ra hay không. Giả sử A là biến cố “Virus A” và B là biến cố “Nhóm tuổi 65+”. Chúng ta muốn biết xác suất của biến cố A biết rằng biến cố B đã xảy ra, được viết là $P (A ∣ B)$ , trong đó dấu gạch đứng | được đọc là “biết rằng”. Đây được gọi là xác suất có điều kiện (conditional probability). Từ dữ liệu trong Bảng 4-1:

Xác suất đồng thời của việc có Virus A và thuộc nhóm tuổi 65+ là:

Biến cố Không xung khắc và Quy tắc Cộng Mở rộng

Nếu hai biến cố không xung khắc, quy tắc cộng phải được sửa đổi; nếu không, xác suất cả hai biến cố cùng xảy ra sẽ được cộng hai lần.

Ví dụ, xác suất là nam hoặc có nhóm máu O là:

Tóm tắt các Quy tắc và Mở rộng

Quy tắc nhân cho các xác suất khi các biến cố không độc lập có thể được sử dụng để suy ra một dạng của công thức quan trọng gọi là định lý Bayes (Bayes’ theorem).

Trong phương trình này, $P (B)$ đôi khi được gọi là xác suất tiền nghiệm (prior probability), vì giá trị của nó được biết trước khi tính toán; $P (B ∣ D)$ được gọi là xác suất hậu nghiệm (posterior probability), vì giá trị của nó chỉ được biết sau khi tính toán.

QUẦN THỂ & MẪU

Một mục đích chính của việc thực hiện nghiên cứu là để suy luận (infer), hay khái quát hóa (generalize), từ một mẫu (sample) cho một quần thể (population) lớn hơn.

Lý do Lấy mẫu

Có ít nhất sáu lý do để nghiên cứu mẫu thay vì toàn bộ quần thể:

Mẫu có thể được nghiên cứu nhanh hơn.
Nghiên cứu mẫu ít tốn kém hơn.
Nghiên cứu toàn bộ quần thể (tổng điều tra) là không thể trong hầu hết các tình huống.
Kết quả từ mẫu thường chính xác hơn.
Nếu mẫu được chọn đúng cách, các phương pháp xác suất có thể được sử dụng để ước tính sai số.
Mẫu có thể được chọn để giảm tính không đồng nhất.

Các Phương pháp Lấy mẫu

Cách tốt nhất để đảm bảo một mẫu sẽ dẫn đến các suy luận đáng tin cậy và hợp lệ là sử dụng mẫu xác suất (probability samples), trong đó xác suất được đưa vào mẫu là đã biết đối với mỗi đối tượng trong quần thể. Bốn phương pháp lấy mẫu xác suất thường được sử dụng trong y học là lấy mẫu ngẫu nhiên đơn giản, lấy mẫu hệ thống, lấy mẫu phân tầng và lấy mẫu theo cụm.

Lấy mẫu ngẫu nhiên đơn giản (Simple Random Sampling): Là phương pháp trong đó mọi đối tượng đều có xác suất được chọn như nhau.

Lấy mẫu hệ thống (Systematic Sampling): Là phương pháp trong đó mọi đối tượng thứ k được chọn; k được xác định bằng cách chia số lượng đối tượng trong khung lấy mẫu cho cỡ mẫu mong muốn.

Lấy mẫu phân tầng (Stratified Sampling): Là phương pháp trong đó quần thể trước tiên được chia thành các tầng (strata) (phân nhóm) có liên quan, và sau đó một mẫu ngẫu nhiên được chọn từ mỗi tầng.

Lấy mẫu theo cụm (Cluster Sampling): Là kết quả của một quy trình hai giai đoạn, trong đó quần thể được chia thành các cụm (clusters) và một tập hợp con các cụm được chọn ngẫu nhiên.

Phân bổ ngẫu nhiên (Random Assignment): Trong các nghiên cứu thực nghiệm như thử nghiệm lâm sàng ngẫu nhiên, các đối tượng trước tiên được chọn để đưa vào nghiên cứu dựa trên các tiêu chí phù hợp; sau đó họ được phân bổ (assigned) vào các phương pháp điều trị khác nhau. Nếu việc phân bổ đối tượng vào các phương pháp điều trị được thực hiện bằng các phương pháp ngẫu nhiên, quá trình này được gọi là phân bổ ngẫu nhiên.

Sử dụng và Diễn giải các Mẫu ngẫu nhiên

Trong các nghiên cứu lâm sàng thực tế, bệnh nhân không phải lúc nào cũng được chọn ngẫu nhiên từ quần thể mà nhà điều tra muốn suy luận. Thay vào đó, nhà nghiên cứu lâm sàng thường sử dụng tất cả các bệnh nhân có sẵn đáp ứng các tiêu chí tham gia nghiên cứu. Quần thể mục tiêu (target population) là quần thể mà nhà điều tra muốn khái quát hóa; quần thể được lấy mẫu (sampled population) là quần thể mà từ đó mẫu thực sự được rút ra. Hình 4-1 trình bày một sơ đồ về các khái niệm này.

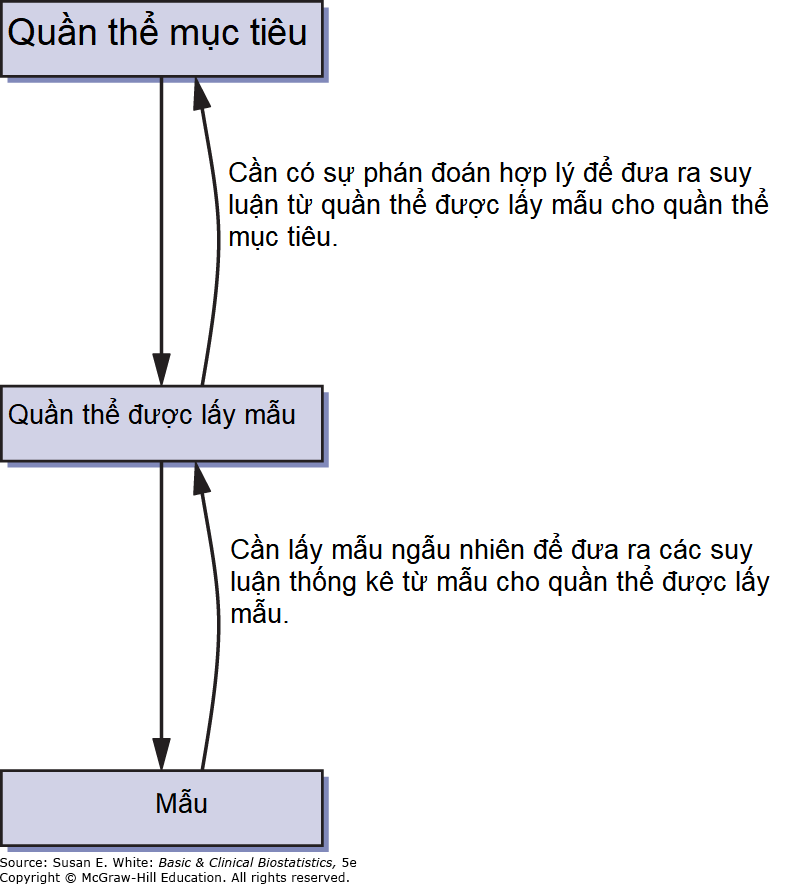
Hình 4-1. Quần thể mục tiêu và quần thể được lấy mẫu.

Tham số Quần thể & Thống kê Mẫu

Các nhà thống kê sử dụng ngôn ngữ chính xác để mô tả các đặc điểm của quần thể và mẫu. Các thước đo về xu hướng trung tâm và biến thiên, chẳng hạn như trung bình và độ lệch chuẩn, là các đặc điểm cố định và bất biến trong các quần thể và được gọi là tham số (parameters). Tuy nhiên, trong các mẫu, trung bình hoặc độ lệch chuẩn quan sát được tính toán trên cơ sở thông tin mẫu thực sự là một ước tính (estimate) của trung bình hoặc độ lệch chuẩn của quần thể; những ước tính này được gọi là thống kê (statistics). Các nhà thống kê thường sử dụng các chữ cái Hy Lạp cho các tham số quần thể và các chữ cái La Mã cho các thống kê mẫu.

Bảng 4-4. Các ký hiệu thường được sử dụng cho tham số và thống kê.

Đặc điểm	Ký hiệu Tham số	Ký hiệu Thống kê
Trung bình	$μ$	$X ˉ$
Độ lệch chuẩn	$σ$	SD
Phương sai	$σ^{2}$	$S^{2}$
Tương quan	$ρ$	r
Tỷ lệ	$π$	p

BIẾN NGẪU NHIÊN & PHÂN PHỐI XÁC SUẤT

Đặc điểm quan tâm trong một nghiên cứu được gọi là một biến (variable). Một biến ngẫu nhiên (random variable) là một biến trong một nghiên cứu trong đó các đối tượng được chọn ngẫu nhiên. Giống như các giá trị của các đặc điểm có thể được tóm tắt trong các phân phối tần suất, các giá trị của một biến ngẫu nhiên có thể được tóm tắt trong một phân phối tần suất được gọi là phân phối xác suất (probability distribution).

Phân phối Nhị thức

Giả sử một biến cố chỉ có thể có các kết quả nhị phân (ví dụ, có và không, hoặc dương và âm). Phân phối nhị thức (binomial distribution) cho xác suất một kết quả cụ thể xảy ra trong một số lần thử độc lập nhất định. Xác suất của X kết quả trong một nhóm có kích thước n, nếu mỗi kết quả có xác suất $π$ và độc lập với tất cả các kết quả khác, được cho bởi công thức:

trong đó ! là ký hiệu cho giai thừa.

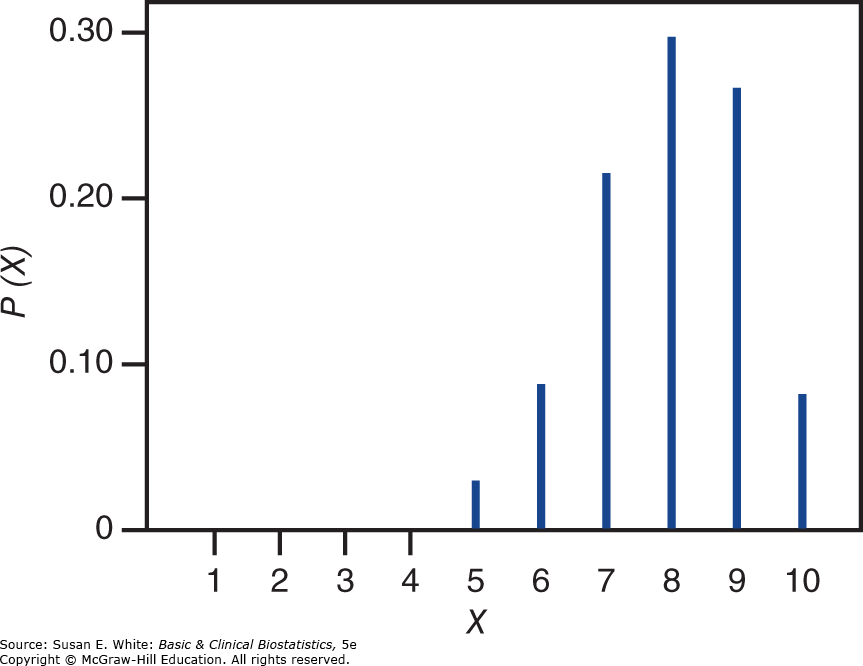
Hình 4-2. Phân phối nhị thức cho n=10 và $π = 0.8$ .

Bảng 4-6. Xác suất cho phân phối nhị thức với n=10 và $π = 0.8$ .

Số bệnh nhân sống sót	$n! / [X! (n - X)!]$	$π^{X}$	$(1 - π)^{n - X}$	P(X)
0	1	0.0000001	1	0.0000
1	10	0.0000005	0.8	0.0000
…	…	…	…	…
8	45	0.168	0.04	0.3020
9	10	0.134	0.2	0.2684
10	1	0.107	1	0.1074

Phân phối Poisson

Phân phối Poisson (Poisson distribution) là một phân phối rời rạc áp dụng khi kết quả là số lần một biến cố xảy ra. Nó có thể được sử dụng để xác định xác suất của các biến cố hiếm gặp. Xác suất của chính xác X lần xảy ra được cho bởi công thức:

trong đó $λ$ (lambda) là giá trị của cả trung bình và phương sai của phân phối Poisson, và $e$ là cơ số của logarit tự nhiên.

Bảng 4-7. Xác suất cho phân phối Poisson với $λ = 3.22$ .

Số lần nhập viện (x)	$λ^{x}$	$e^{- λ}$	x!	P(X)
0	1	0.040	1	0.040
1	3.22	0.040	1	0.129
…	…	…	…	…
7	3589.15	0.040	5040	0.028

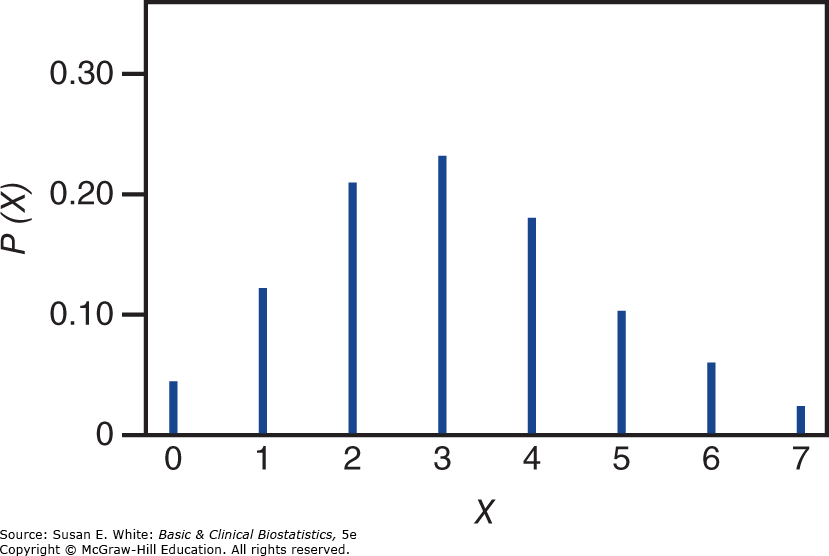
Hình 4-3. Phân phối Poisson cho $λ = 3.22$ .

Phân phối Chuẩn (Gaussian)

Phân phối chuẩn (normal distribution), hay đường cong Gaussian (hoặc hình chuông), là một phân phối xác suất liên tục. Nó là một đường cong trơn, hình chuông và đối xứng quanh giá trị trung bình của phân phối, ký hiệu là $μ$ (mu). Độ lệch chuẩn của phân phối được ký hiệu là $σ$ (sigma).

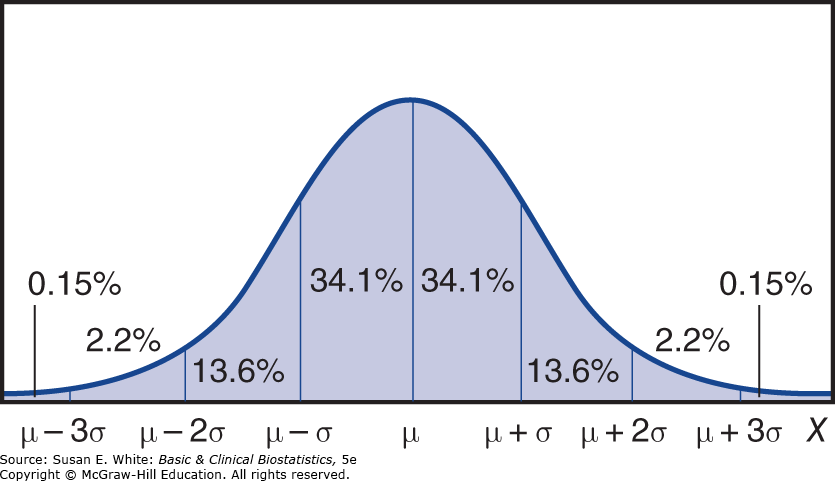
Hình 4-4. Phân phối chuẩn và tỷ lệ phần trăm diện tích dưới đường cong.

Phân phối Chuẩn tắc (z)

Phân phối chuẩn tắc (standard normal curve) (phân phối z) có trung bình là 0 và độ lệch chuẩn là 1, như trong Hình 4-6. Bất kỳ phân phối chuẩn nào cũng có thể được chuyển đổi thành phân phối chuẩn tắc bằng cách sử dụng phép biến đổi z:

$z = σ X - μ$

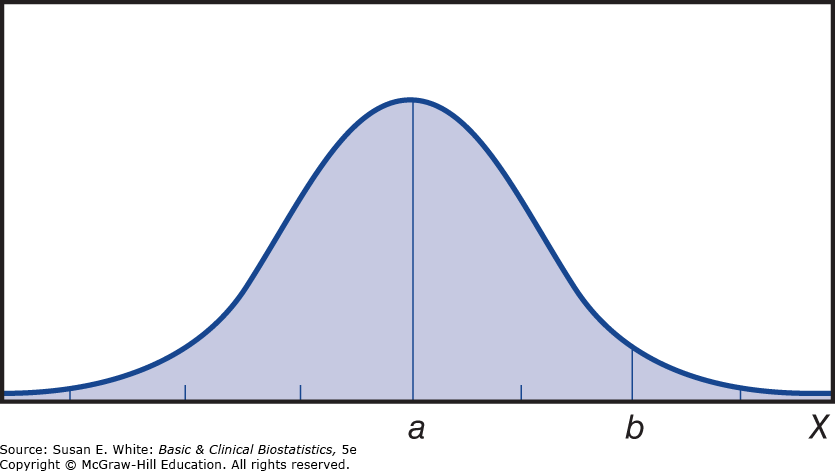
Hình 4-5. Diện tích dưới đường cong chuẩn giữa a và b.

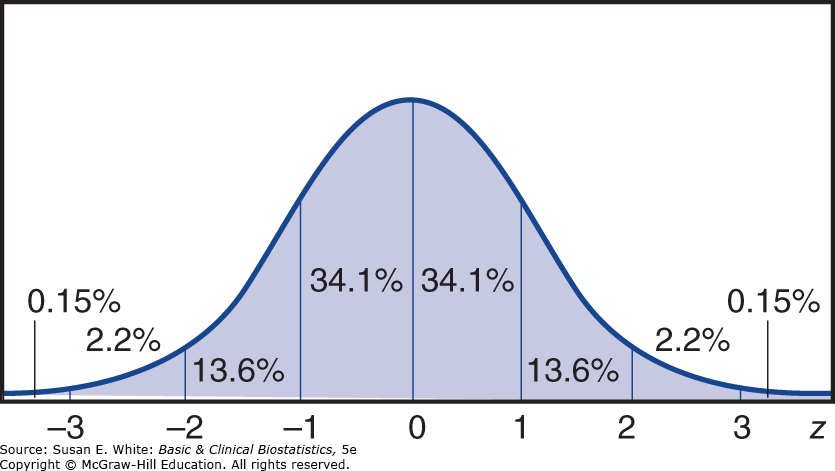
Hình 4-6. Phân phối chuẩn tắc (z).

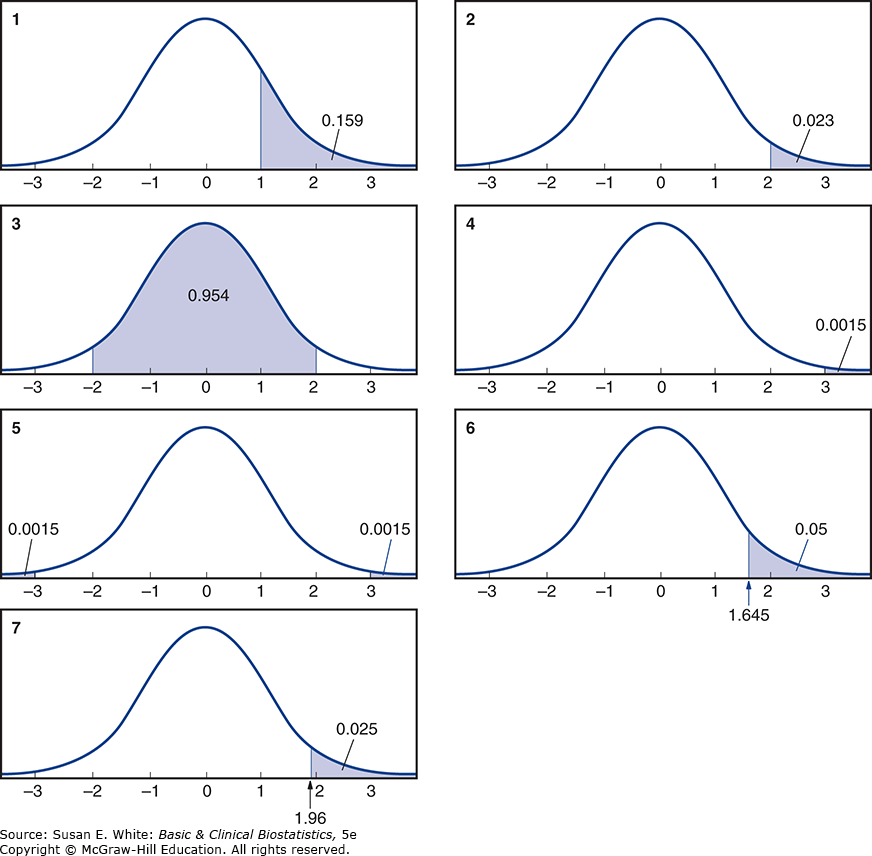
Hình 4-7. Tìm diện tích dưới đường cong bằng cách sử dụng phân phối chuẩn.

PHÂN PHỐI LẤY MẪU

Phân phối Lấy mẫu của Trung bình

Phân phối lấy mẫu của trung bình (sampling distribution of the mean) là phân phối của các giá trị trung bình được tính từ nhiều mẫu được rút ra từ cùng một quần thể.

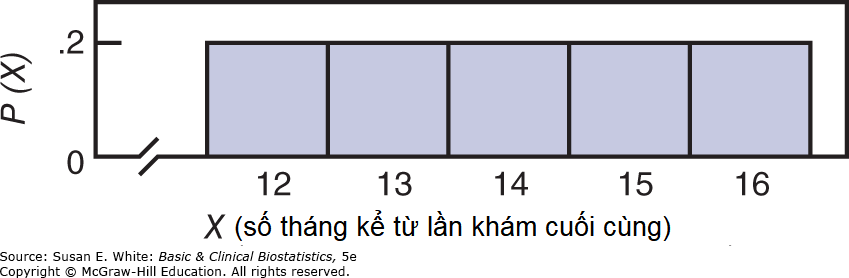
Hình 4-8. Phân phối các giá trị của quần thể về số tháng kể từ lần khám cuối cùng (dữ liệu từ Bảng 4-8).

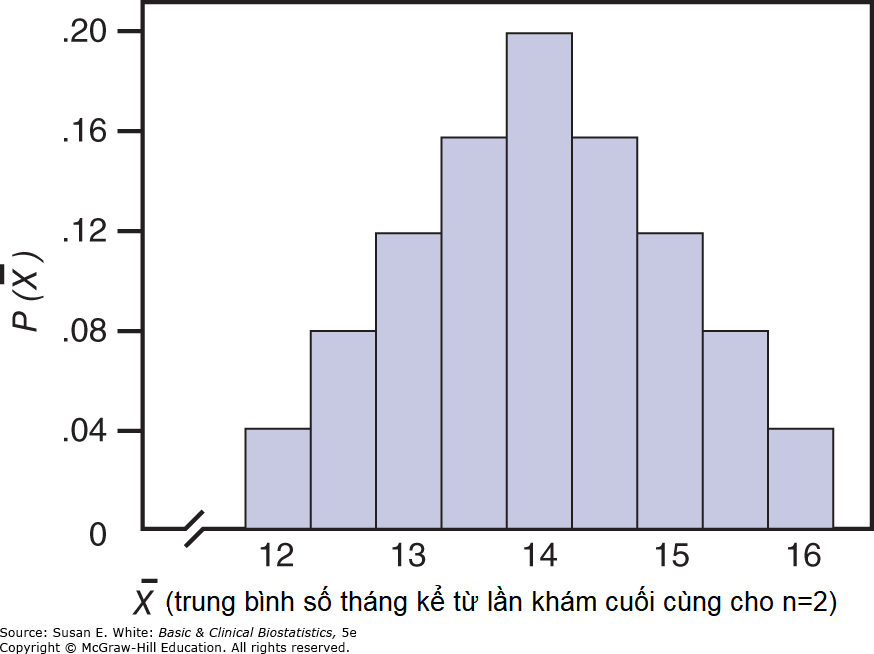
Hình 4-9. Phân phối của trung bình số tháng kể từ lần khám cuối cùng cho n=2 (dữ liệu từ Bảng 4-9).

Định lý Giới hạn Trung tâm

Định lý giới hạn trung tâm (central limit theorem) là một trong những định lý quan trọng nhất trong thống kê. Nó phát biểu rằng:

Cho một quần thể có trung bình $μ$ và độ lệch chuẩn $σ$ , phân phối lấy mẫu của trung bình dựa trên các mẫu ngẫu nhiên lặp lại có kích thước n có các thuộc tính sau:

Trung bình của phân phối lấy mẫu bằng với trung bình của quần thể $μ$ .
Độ lệch chuẩn trong phân phối lấy mẫu của trung bình bằng $σ / n$ . Đại lượng này được gọi là sai số chuẩn của trung bình (standard error of the mean – SEM).
Nếu phân phối trong quần thể là chuẩn, thì phân phối lấy mẫu của trung bình cũng là chuẩn. Quan trọng hơn, đối với các cỡ mẫu đủ lớn, phân phối lấy mẫu của trung bình xấp xỉ phân phối chuẩn, bất kể hình dạng của phân phối quần thể ban đầu.

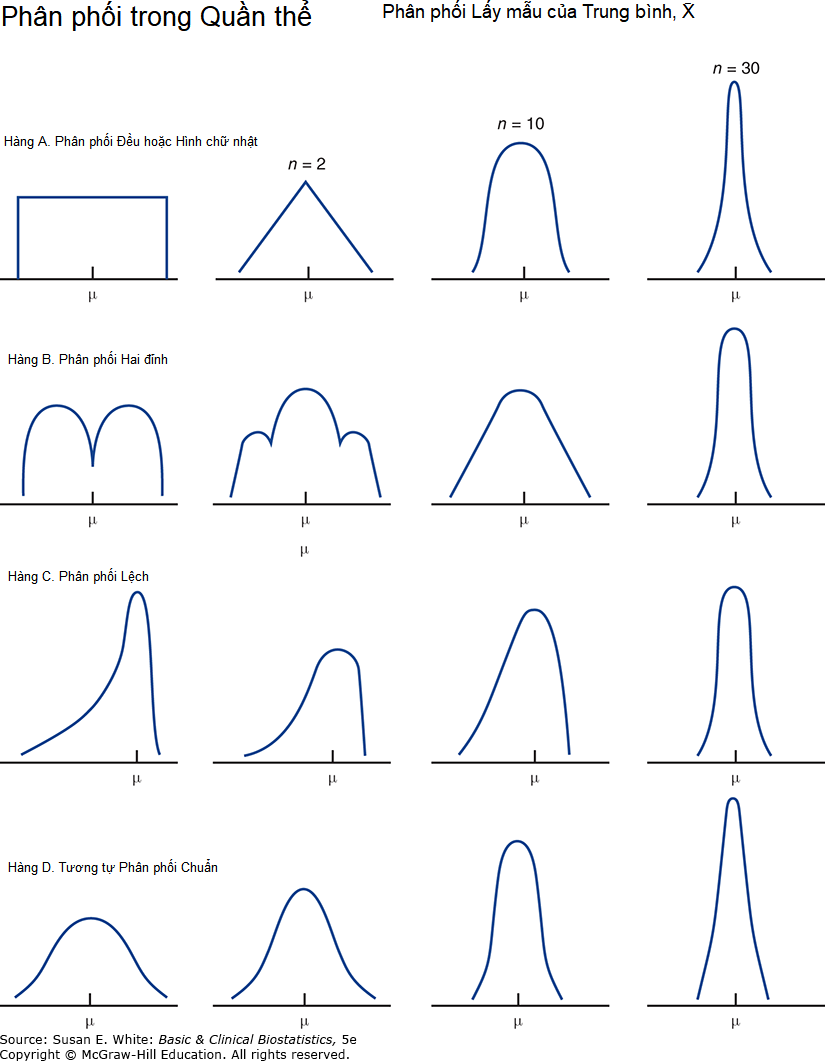
Hình 4-10. Minh họa các hệ quả của định lý giới hạn trung tâm.

Độ lệch chuẩn so với Sai số chuẩn:

Giá trị $σ$ đo lường độ lệch chuẩn trong quần thể và dựa trên các phép đo của các cá nhân. Sai số chuẩn của trung bình, tuy nhiên, là độ lệch chuẩn của các giá trị trung bình trong một phân phối lấy mẫu; nó cho chúng ta biết mức độ biến thiên có thể được mong đợi giữa các giá trị trung bình trong các mẫu trong tương lai.

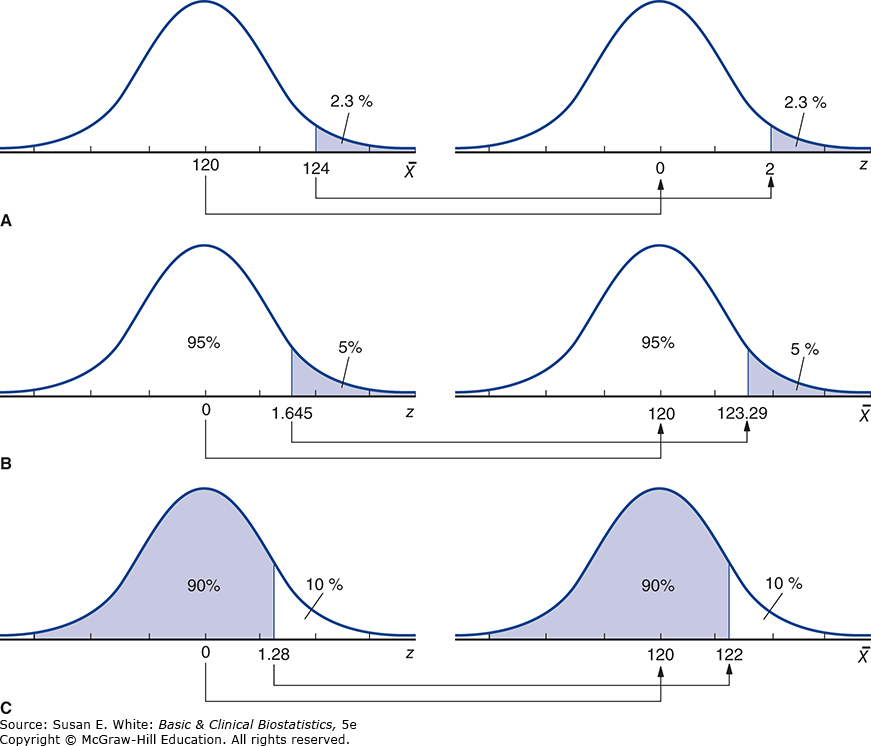
Hình 4-11. Sử dụng phân phối chuẩn để rút ra kết luận về huyết áp tâm thu ở người lớn khỏe mạnh.

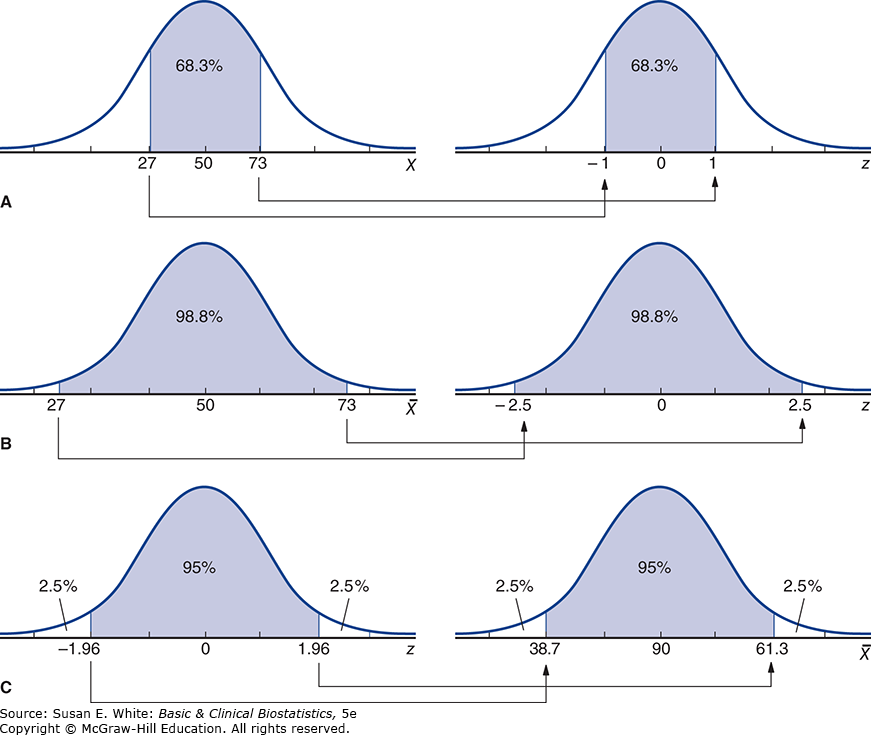
Hình 4-12. Sử dụng phân phối chuẩn để rút ra kết luận về mức độ PO2 ở người lớn khỏe mạnh.

ƯỚC LƯỢNG & KIỂM ĐỊNH GIẢ THUYẾT

Có hai cách tiếp cận để suy luận thống kê: ước lượng (estimating) các tham số và kiểm định giả thuyết (testing hypotheses).

Sự cần thiết của các Ước tính

Thay vì nghiên cứu toàn bộ quần thể, chúng ta tiến hành một nghiên cứu trên một mẫu ngẫu nhiên. Tỷ lệ hoặc trung bình trong mẫu được sử dụng như một ước tính điểm (point estimate) của tỷ lệ hoặc trung bình trong quần thể.

Thuộc tính của các Ước tính Tốt

Một ước tính tốt nên không chệch (unbiased) và có phương sai nhỏ nhất (minimum variance).

Khoảng tin cậy và Giới hạn Tin cậy:

Thay vì đưa ra một ước tính điểm đơn giản, các nhà điều tra sử dụng ước tính khoảng (interval estimates). Các ước tính khoảng được gọi là khoảng tin cậy (confidence intervals); chúng xác định một giới hạn trên (upper limit) và một giới hạn dưới (lower limit) với một xác suất liên quan.

Kiểm định Giả thuyết

Kiểm định giả thuyết thống kê (statistical hypothesis testing) bao gồm việc phát biểu một giả thuyết không (null hypothesis) và một giả thuyết thay thế (alternative hypothesis) và sau đó thực hiện một kiểm định thống kê để xem giả thuyết nào nên được kết luận.

TÓM TẮT Ý CHÍNH

Chương này tập trung vào một số khái niệm giải thích tại sao kết quả của một nghiên cứu liên quan đến một tập hợp đối tượng nhất định có thể được sử dụng để rút ra kết luận về các đối tượng tương tự khác. Những khái niệm này bao gồm xác suất, lấy mẫu, phân phối xác suất và phân phối lấy mẫu.

Ba phân phối xác suất quan trọng đã được trình bày: nhị thức, Poisson và chuẩn (Gaussian). Phân phối nhị thức được sử dụng để mô hình hóa các biến cố có kết quả nhị phân. Phân phối Poisson được sử dụng để xác định xác suất cho các biến cố hiếm gặp. Phân phối chuẩn được sử dụng để xác định xác suất của các đặc điểm được đo trên thang đo số lượng liên tục.

Ước lượng và kiểm định giả thuyết là hai phương pháp để đưa ra suy luận về một giá trị trong một quần thể đối tượng bằng cách sử dụng các quan sát từ một mẫu ngẫu nhiên các đối tượng. Trong các chương tiếp theo, chúng tôi sẽ minh họa cả khoảng tin cậy và kiểm định giả thuyết.

BÀI TẬP THỰC HÀNH

a. Chứng minh rằng giới tính và nhóm máu là độc lập, tức là, xác suất đồng thời là tích của hai xác suất biên cho mỗi ô trong Bảng 4-2. b. Điều gì xảy ra nếu bạn sử dụng quy tắc nhân với xác suất có điều kiện khi hai biến cố là độc lập?
“Thiếu máu bất sản” đề cập đến tình trạng giảm ba dòng tế bào máu nghiêm trọng. Sử dụng Bảng 4-10 để trả lời các câu hỏi sau: a. Xác suất của bệnh ghép chống chủ mãn tính là gì? b. Xác suất của bệnh ghép chống chủ cấp tính là gì? c. Nếu một bệnh nhân chuyển đổi huyết thanh, xác suất bệnh nhân đó mắc bệnh ghép chống chủ cấp tính là gì? d. Khả năng một bệnh nhân đã chết có huyết thanh dương tính là bao nhiêu? e. Tỷ lệ bệnh nhân có huyết thanh âm tính là bao nhiêu?

Bảng 4-10. Tỷ lệ mới mắc của bệnh ghép chống chủ.

Tình trạng	Âm tính huyết thanh	Chuyển đổi huyết thanh	Dương tính huyết thanh
Bệnh ghép chống chủ cấp tính	6/17	2/8	2/12
Bệnh ghép chống chủ mãn tính	7/17	3/8	2/12
Tử vong	3/17	3/8	2/12

Sao chép với sự cho phép từ Anasetti C, và cộng sự (1986).

Tham khảo Bảng 4-1 về 48,291 bệnh nhân. Giả sử một bệnh nhân được chọn ngẫu nhiên. a. Xác suất một bệnh nhân được chọn ngẫu nhiên mắc virus cúm A là gì? b. Xác suất một bệnh nhân được chọn ngẫu nhiên trong nhóm tuổi 25-64 mắc virus cúm B là gì?
Một bác sĩ phẫu thuật thẩm mỹ muốn so sánh số ca ghép da thành công. Một cuộc khảo sát y văn cho thấy khoảng 30% các ca ghép bị nhiễm trùng nhưng 80% sống sót. Bà đã có 7 trong 8 ca ghép da sống sót và có một ca nhiễm trùng. a. Khả năng chỉ có 1 trong 8 ca nhiễm trùng là bao nhiêu? b. Khả năng sống sót trong 7 trong 8 ca ghép là bao nhiêu?
Sử dụng phân phối Poisson để ước tính xác suất một bệnh nhân phẫu thuật sẽ có năm lần nhập viện trong 10 năm theo dõi nếu một mẫu 390 bệnh nhân phẫu thuật có tổng cộng 1.487 lần nhập viện.
Các giá trị natri huyết thanh ở người lớn khỏe mạnh xấp xỉ tuân theo phân phối chuẩn với trung bình là 141 mEq/L và độ lệch chuẩn là 3 mEq/L. a. Xác suất một người lớn khỏe mạnh bình thường sẽ có giá trị natri huyết thanh trên 147 mEq/L là gì? b. Xác suất một người lớn khỏe mạnh bình thường sẽ có giá trị natri huyết thanh dưới 130 mEq/L là gì? c. Xác suất một người lớn khỏe mạnh bình thường sẽ có giá trị natri huyết thanh từ 132 đến 150 mEq/L là gì? d. Mức natri huyết thanh nào là cần thiết để đưa một người vào top 1% của phân phối? e. Mức natri huyết thanh nào là cần thiết để đưa một người vào bottom 10% của phân phối?
Tính toán phân phối nhị thức cho mỗi bộ tham số: n=6, $π = 0.1$ ; n=6, $π = 0.2$ ; n=6, $π = 0.5$ . Vẽ đồ thị của mỗi phân phối và nêu kết luận của bạn về hình dạng của chúng.
a. Tính trung bình và độ lệch chuẩn của số tháng kể từ lần khám cuối cùng của bệnh nhân từ Bảng 4-8. b. Tính trung bình và độ lệch chuẩn của phân phối lấy mẫu của trung bình số tháng từ Bảng 4-9.
Giả sử clorua huyết thanh có trung bình là 100 mEq/L và độ lệch chuẩn là 3 trong các quần thể khỏe mạnh bình thường. a. Tỷ lệ dân số có mức clorua huyết thanh lớn hơn 103 và nhỏ hơn 97 mEq/L là bao nhiêu? b. Nếu các mẫu lặp lại gồm 36 người được chọn, tỷ lệ trong số đó sẽ có trung bình nhỏ hơn 99 và lớn hơn 101 mEq/L là bao nhiêu?
Mối quan hệ giữa việc uống rượu và bệnh vẩy nến chưa rõ ràng. Sử dụng thông tin trong Bảng 4-11 về tần suất say rượu ở bệnh nhân vẩy nến. a. Xác suất một bệnh nhân được chọn ngẫu nhiên từ nhóm 131 người sẽ say rượu hơn hai lần một tuần là bao nhiêu? b. Một bệnh nhân cần phải say rượu bao nhiêu lần một năm để nằm trong top 5% của tất cả các bệnh nhân?

Bảng 4-11. Lượng rượu uống (g/ngày) và tần suất say rượu (lần/năm) trước khi khởi phát bệnh da ở bệnh nhân vẩy nến và nhóm chứng.

	Trung bình	SEM	Số ca	Giá trị p
Lượng rượu uống
Bệnh nhân vẩy nến	42.9	7.2	142	0.004
Đối chứng	21.0	2.1	265
Tần suất say rượu
Bệnh nhân vẩy nến	61.6	6.2	131	0.007
Đối chứng	42.6	3.3	247

Sao chép với sự cho phép từ Poikolainen K, và cộng sự (1990).

Hiệp hội các trường Cao đẳng Y khoa Hoa Kỳ báo cáo rằng nợ năm 2002 của sinh viên tốt nghiệp từ các trường y khoa Hoa Kỳ có trung bình là $104,000 và trung vị là$ 100,000; 5% sinh viên tốt nghiệp có nợ từ $200,000 trở lên. Giả sử nợ được phân phối chuẩn, giá trị gần đúng của độ lệch chuẩn là bao nhiêu?
Từ kinh nghiệm của chính họ tại một bệnh viện công ở thành thị, Kaku và Lowenstein (1990) đã ghi nhận rằng đột quỵ liên quan đến việc sử dụng ma túy giải trí đang xảy ra thường xuyên hơn ở những người trẻ tuổi. Dữ liệu được đưa ra trong Bảng 4-21. Tỷ số chênh là bao nhiêu?

Bảng 4-21. Dữ liệu cho tỷ số chênh đột quỵ với tiền sử lạm dụng thuốc.

	Đột quỵ	Đối chứng
Lạm dụng thuốc	73	18
Không lạm dụng thuốc	141	196
Tổng	214	214

Dữ liệu từ Kaku DA, Lowenstein DH (1990).

Bài tập nhóm. Lấy một bản sao của nghiên cứu của Moore và cộng sự (1991) từ thư viện y khoa của bạn và trả lời các câu hỏi sau: a. Mục đích của nghiên cứu này là gì? b. Thiết kế nghiên cứu là gì? c. Tại sao hai nhóm bệnh nhân được sử dụng trong nghiên cứu? d. Kiểm tra các biểu đồ hộp trong Hình 3-1 của bài báo. Có thể rút ra kết luận gì từ các biểu đồ? e. Kiểm tra các biểu đồ hộp trong Hình 3-2 của bài báo. Các biểu đồ này cho bạn biết điều gì về mức độ pH ở những người đàn ông khỏe mạnh bình thường?
Bài tập nhóm. Điều quan trọng là các thang đo được khuyến nghị cho các bác sĩ sử dụng trong việc đánh giá nguy cơ hoặc đưa ra quyết định quản lý phải được chứng minh là đáng tin cậy và hợp lệ. Chọn một lĩnh vực quan tâm và tham khảo một số bài báo tạp chí mô tả các thang đo hoặc quy tắc quyết định. Đánh giá xem các tác giả có trình bày đủ bằng chứng về khả năng tái lập và tính hợp lệ của các thang đo này không. Loại khả năng tái lập nào đã được thiết lập? Loại tính hợp lệ nào? Những điều này có đủ để đảm bảo việc sử dụng thang đo không?

Bảng chú giải thuật ngữ Anh-Việt: Chương 4

STT	Thuật ngữ tiếng Anh	Phiên âm IPA	Nghĩa Tiếng Việt
1	Probability	/ˌprɒbəˈbɪləti/	Xác suất
2	Inferences	/ˈɪnfərənsɪz/	Suy luận (thống kê)
3	Objective probability	/əbˈdʒɛktɪv ˌprɒbəˈbɪləti/	Xác suất khách quan
4	Subjective probability	/səbˈdʒɛktɪv ˌprɒbəˈbɪləti/	Xác suất chủ quan
5	Event	/ɪˈvɛnt/	Biến cố
6	Outcome	/ˈaʊtˌkʌm/	Kết quả
7	Bayes’ theorem	/beɪz ˈθɪərəm/	Định lý Bayes
8	Conditional probability	/kənˈdɪʃənəl ˌprɒbəˈbɪləti/	Xác suất có điều kiện
9	Diagnostic procedures	/ˌdaɪəɡˈnɒstɪk prəˈsiːdʒərz/	Quy trình chẩn đoán
10	Populations	/ˌpɒpjuˈleɪʃənz/	Quần thể
11	Samples	/ˈsæmpəlz/	Mẫu
12	Sampling	/ˈsæmplɪŋ/	Lấy mẫu
13	Random	/ˈrændəm/	Ngẫu nhiên
14	Random variable	/ˈrændəm ˈvɛəriəbəl/	Biến ngẫu nhiên
15	Statistical tests	/stəˈtɪstɪkəl tɛsts/	Các kiểm định thống kê
16	Binomial distribution	/baɪˈnoʊmiəl ˌdɪstrɪˈbjuːʃən/	Phân phối nhị thức
17	Poisson distribution	/ˈpwɑːsɒn ˌdɪstrɪˈbjuːʃən/	Phân phối Poisson
18	Rare events	/rɛər ɪˈvɛnts/	Biến cố hiếm
19	Normal distribution	/ˈnɔːrməl ˌdɪstrɪˈbjuːʃən/	Phân phối chuẩn
20	Bell-shaped distribution	/bɛl ʃeɪpt ˌdɪstrɪˈbjuːʃən/	Phân phối hình chuông
21	Sampling distribution	/ˈsæmplɪŋ ˌdɪstrɪˈbjuːʃən/	Phân phối lấy mẫu
22	Central limit theorem	/ˈsɛntrəl ˈlɪmɪt ˈθɪərəm/	Định lý giới hạn trung tâm
23	Standard deviation	/ˈstændərd ˌdiːviˈeɪʃən/	Độ lệch chuẩn
24	Standard error of the mean	/ˈstændərd ˈɛrər əv ðə miːn/	Sai số chuẩn của trung bình
25	Estimates	/ˈɛstɪmɪts/	Các ước tính, các ước lượng
26	Confidence intervals	/ˈkɒnfɪdəns ˈɪntərvəlz/	Khoảng tin cậy
27	Neoplasia	/ˌniːəˈpleɪʒə/	Tân sản, khối u
28	Radical prostatectomy	/ˈrædɪkəl ˌprɒstəˈtɛktəmi/	Cắt bỏ tuyến tiền liệt triệt để
29	Salvage radiation therapy	/ˈsælvɪdʒ ˌreɪdiˈeɪʃən ˈθɛrəpi/	Xạ trị cứu vớt
30	Antiandrogen therapy	/ˌæntiˈændrədʒən ˈθɛrəpi/	Liệu pháp kháng androgen
31	Prospective	/prəˈspɛktɪv/	Tiến cứu
32	Randomized	/ˈræəndəmaɪzd/	Ngẫu nhiên hóa
33	Multicenter collaborative trial	/ˌmʌltiˈsɛntər kəˈlæbərətɪv ˈtraɪəl/	Thử nghiệm hợp tác đa trung tâm
34	Stable ischemic heart disease	/ˈsteɪbəl ɪˈskiːmɪk hɑːrt dɪˈziːz/	Bệnh tim thiếu máu cục bộ ổn định
35	Coronary revascularization	/ˈkɒrənəri ˌriːˌvæskjələraɪˈzeɪʃən/	Tái thông mạch vành
36	Quality of life	/ˈkwɒlɪti əv laɪf/	Chất lượng cuộc sống
37	Clinical subsets	/ˈklɪnɪkəl ˈsʌbˌsɛts/	Các phân nhóm lâm sàng
38	Stenosis	/stɪˈnoʊsɪs/	Hẹp
39	Left main coronary artery	/lɛft meɪn ˈkɒrənəri ˈɑːrtəri/	Động mạch vành chính trái
40	Ejection fraction	/ɪˈdʒɛkʃən ˈfrækʃən/	Phân suất tống máu
41	Myocardial infarction	/ˌmaɪəˈkɑːrdiəl ɪnˈfɑːrkʃən/	Nhồi máu cơ tim
42	Treadmill testing	/ˈtrɛdˌmɪl ˈtɛstɪŋ/	Trắc nghiệm gắng sức trên thảm lăn
43	Follow-up questionnaire	/ˈfɒloʊ ʌp ˌkwɛstʃəˈnɛər/	Bảng câu hỏi theo dõi
44	Chest pain status	/tʃɛst peɪn ˈsteɪtəs/	Tình trạng đau ngực
45	Heart failure	/hɑːrt ˈfeɪljər/	Suy tim
46	Activity limitation	/ækˈtɪvɪti ˌlɪmɪˈteɪʃən/	Hạn chế hoạt động
47	Employment status	/ɪmˈplɔɪmənt ˈsteɪtəs/	Tình trạng việc làm
48	Recreational status	/ˌrɛkriˈeɪʃənəl ˈsteɪtəs/	Tình trạng giải trí
49	Drug therapy	/drʌɡ ˈθɛrəpi/	Liệu pháp dùng thuốc
50	Hospitalizations	/ˌhɒspɪtəlaɪˈzeɪʃənz/	Số lần nhập viện
51	Risk factor alteration	/rɪsk ˈfæktər ˌɔːltəˈreɪʃən/	Thay đổi yếu tố nguy cơ
52	BP control	/biː piː kənˈtroʊl/	Kiểm soát huyết áp
53	Cholesterol level	/kəˈlɛstəˌrɒl ˈlɛvəl/	Mức cholesterol
54	Poisson probability distribution	/ˈpwɑːsɒn ˌprɒbəˈbɪləti ˌdɪstrɪˈbjuːʃən/	Phân phối xác suất Poisson
55	Generalize	/ˈdʒɛnərəˌlaɪz/	Khái quát hóa
56	Inferences	/ˈɪnfərənsɪz/	Các suy luận
57	Overall survival	/ˌoʊvərˈɔːl sərˈvaɪvəl/	Sống còn toàn bộ
58	Placebo	/pləˈsiːboʊ/	Giả dược
59	t test	/tiː tɛst/	Kiểm định t
60	Significantly greater	/sɪɡˈnɪfɪkəntli ˈɡreɪtər/	Lớn hơn một cách có ý nghĩa
61	Alpha value (α)	/ˈælfə ˈvæljuː/	Giá trị alpha (α)
62	Power (of a study)	/ˈpaʊər (əv ə ˈstʌdi)/	Lực (của một nghiên cứu)
63	Experiment	/ɪkˈspɛrɪmənt/	Thí nghiệm
64	Replication	/ˌrɛplɪˈkeɪʃən/	Sự lặp lại
65	Trial	/ˈtraɪəl/	Phép thử
66	Empirically	/ɪmˈpɪrɪkli/	Theo kinh nghiệm
67	Theoretical model	/ˌθiːəˈrɛtɪkəl ˈmɒdəl/	Mô hình lý thuyết
68	Fair coin	/fɛər kɔɪn/	Đồng xu cân đối
69	Hunch	/hʌntʃ/	Linh cảm
70	Complementary event	/ˌkɒmplɪˈmɛntəri ɪˈvɛnt/	Biến cố bù
71	Mutually exclusive events	/ˈmjuːtʃuəli ɪkˈskluːsɪv ɪˈvɛnts/	Các biến cố xung khắc
72	Addition rule	/əˈdɪʃən ruːl/	Quy tắc cộng
73	Independent events	/ˌɪndɪˈpɛndənt ɪˈvɛnts/	Các biến cố độc lập
74	Multiplication rule	/ˌmʌltɪplɪˈkeɪʃən ruːl/	Quy tắc nhân
75	Marginal probabilities	/ˈmɑːrdʒɪnəl ˌprɒbəˈbɪlətiz/	Xác suất biên
76	Joint probability	/dʒɔɪnt ˌprɒbəˈbɪləti/	Xác suất đồng thời
77	Nonindependent events	/nɒn ˌɪndɪˈpɛndənt ɪˈvɛnts/	Các biến cố không độc lập
78	Conditional probability	/kənˈdɪʃənəl ˌprɒbəˈbɪləti/	Xác suất có điều kiện
79	Nonmutually exclusive events	/nɒn ˈmjuːtʃuəli ɪkˈskluːsɪv ɪˈvɛnts/	Các biến cố không xung khắc
80	Prior probability	/ˈpraɪər ˌprɒbəˈbɪləti/	Xác suất tiền nghiệm
81	Posterior probability	/pɒˈstɪəriər ˌprɒbəˈbɪləti/	Xác suất hậu nghiệm
82	Odds	/ɒdz/	Tỷ suất chênh (odds)
83	Likelihood	/ˈlaɪkliˌhʊd/	Khả năng, hợp lý
84	Hypotheses	/haɪˈpɒθəsiːz/	Các giả thuyết
85	Sample	/ˈsæmpəl/	Mẫu
86	Population	/ˌpɒpjuˈleɪʃən/	Quần thể
87	Representative	/ˌrɛprɪˈzɛntətɪv/	Có tính đại diện
88	Census	/ˈsɛnsəs/	Tổng điều tra
89	Histologic studies	/ˌhɪstəˈlɒdʒɪk ˈstʌdiz/	Nghiên cứu mô học
90	Heterogeneity	/ˌhɛtərəʊdʒɪˈniːɪti/	Tính không đồng nhất
91	Power of a study	/ˈpaʊər əv ə ˈstʌdi/	Lực của một nghiên cứu
92	Probability samples	/ˌprɒbəˈbɪləti ˈsæmpəlz/	Mẫu xác suất
93	Simple random sampling	/ˈsɪmpəl ˈrændəm ˈsæmplɪŋ/	Lấy mẫu ngẫu nhiên đơn giản
94	Systematic sampling	/ˌsɪstɪˈmætɪk ˈsæmplɪŋ/	Lấy mẫu hệ thống
95	Stratified sampling	/ˈstrætɪˌfaɪd ˈsæmplɪŋ/	Lấy mẫu phân tầng
96	Cluster sampling	/ˈklʌstər ˈsæmplɪŋ/	Lấy mẫu theo cụm
97	Intrarater reliability	/ˌɪntrəˈreɪtər rɪˌlaɪəˈbɪləti/	Độ tin cậy nội người đánh giá
98	Sampling frame	/ˈsæmplɪŋ freɪm/	Khung lấy mẫu
99	Cyclic repetition	/ˈsaɪklɪk ˌrɛpɪˈtɪʃən/	Sự lặp lại có chu kỳ
100	Strata	/ˈstrɑːtə/	Các tầng
101	Nonprobability sampling	/nɒn ˌprɒbəˈbɪləti ˈsæmplɪŋ/	Lấy mẫu phi xác suất
102	Convenience samples	/kənˈviːniəns ˈsæmpəlz/	Mẫu thuận tiện
103	Quota samples	/ˈkwoʊtə ˈsæmpəlz/	Mẫu theo chỉ tiêu
104	Selection biases	/sɪˈlɛkʃən ˈbaɪəsɪz/	Sai lệch do chọn mẫu
105	Random assignment	/ˈrændəm əˈsaɪnmənt/	Phân bổ ngẫu nhiên
106	Treatment modalities	/ˈtriːtmənt moʊˈdælətiz/	Các phương thức điều trị
107	Balanced (assignment)	/ˈbælənst (əˈsaɪnmənt)/	(Phân bổ) cân bằng
108	Blocks (in randomization)	/blɒks (ɪn ˌrændəmaɪˈzeɪʃən)/	Khối (trong ngẫu nhiên hóa)
109	Stratified assignment	/ˈstrætɪˌfaɪd əˈsaɪnmənt/	Phân bổ theo tầng
110	Confounding effects	/kənˈfaʊndɪŋ ɪˈfɛkts/	Các tác động gây nhiễu
111	Target population	/ˈtɑːrɡɪt ˌpɒpjuˈleɪʃən/	Quần thể mục tiêu
112	Sampled population	/ˈsæmpəld ˌpɒpjuˈleɪʃən/	Quần thể được lấy mẫu
113	Parameters	/pəˈræmɪtərz/	Tham số
114	Statistics	/stəˈtɪstɪks/	Thống kê (số nhiều)
115	Variable	/ˈvɛəriəbəl/	Biến số
116	Measurement errors	/ˈmɛʒərmənt ˈɛrərz/	Sai số đo lường
117	Random variable	/ˈrændəm ˈvɛəriəbəl/	Biến ngẫu nhiên
118	Probability distribution	/ˌprɒbəˈbɪləti ˌdɪstrɪˈbjuːʃən/	Phân phối xác suất
119	Discrete probability distributions	/dɪˈskriːt ˌprɒbəˈbɪləti ˌdɪstrɪˈbjuːʃənz/	Các phân phối xác suất rời rạc
120	Continuous probability distribution	/kənˈtɪnjuəs ˌprɒbəˈbɪləti ˌdɪstrɪˈbjuːʃən/	Phân phối xác suất liên tục
121	Gaussian distribution	/ˈɡaʊsiən ˌdɪstrɪˈbjuːʃən/	Phân phối Gaussian
122	Bernoulli trial	/bərˈnuːli ˈtraɪəl/	Phép thử Bernoulli
123	Factorial	/fækˈtɔːriəl/	Giai thừa
124	Combinations	/ˌkɒmbɪˈneɪʃənz/	Tổ hợp
125	Parameters (of a distribution)	/pəˈræmɪtərz (əv ə ˌdɪstrɪˈbjuːʃən)/	Tham số (của một phân phối)
126	Natural logarithms	/ˈnætʃərəl ˈlɒɡəˌrɪðəmz/	Logarit tự nhiên
127	Point of inflection	/pɔɪnt əv ɪnˈflɛkʃən/	Điểm uốn
128	Standard normal curve	/ˈstændərd ˈnɔːrməl kɜːrv/	Đường cong chuẩn tắc
129	z distribution	/ziː ˌdɪstrɪˈbjuːʃən/	Phân phối z
130	z transformation	/ziː ˌtrænsfərˈmeɪʃən/	Phép biến đổi z
131	z score	/ziː skɔːr/	Điểm z
132	Normal deviate	/ˈnɔːrməl ˈdiːviət/	Độ lệch chuẩn
133	Standard score	/ˈstændərd skɔːr/	Điểm chuẩn
134	Critical ratio	/ˈkrɪtɪkəl ˈreɪʃioʊ/	Tỷ số tới hạn
135	Sampling distribution	/ˈsæmplɪŋ ˌdɪstrɪˈbjuːʃən/	Phân phối lấy mẫu
136	Uniform distribution	/ˈjuːnɪˌfɔːrm ˌdɪstrɪˈbjuːʃən/	Phân phối đều
137	Rectangular distribution	/rɛkˈtæŋɡjələr ˌdɪstrɪˈbjuːʃən/	Phân phối hình chữ nhật
138	Pyramid shape	/ˈpɪrəmɪd ʃeɪp/	Hình kim tự tháp
139	Standard error of the mean (SEM)	/ˈstændərd ˈɛrər əv ðə miːn/	Sai số chuẩn của trung bình
140	Parent population	/ˈpɛərənt ˌpɒpjuˈleɪʃən/	Quần thể gốc
141	t distribution	/tiː ˌdɪstrɪˈbjuːʃən/	Phân phối t
142	F distribution	/ɛf ˌdɪstrɪˈbjuːʃən/	Phân phối F
143	Standard error of the statistic	/ˈstændərd ˈɛrər əv ðə stəˈtɪstɪk/	Sai số chuẩn của thống kê
144	Vasoconstriction	/ˌveɪzoʊkənˈstrɪkʃən/	Co mạch
145	Estimation	/ˌɛstɪˈmeɪʃən/	Ước lượng
146	Hypothesis testing	/haɪˈpɒθəsɪs ˈtɛstɪŋ/	Kiểm định giả thuyết
147	Point estimates	/pɔɪnt ˈɛstɪmɪts/	Ước lượng điểm
148	Unbiased	/ʌnˈbaɪəst/	Không chệch
149	Systematic error	/ˌsɪstɪˈmætɪk ˈɛrər/	Sai số hệ thống
150	Minimum variance	/ˈmɪnɪməm ˈvɛəriəns/	Phương sai nhỏ nhất
151	Interval estimates	/ˈɪntərvəl ˈɛstɪmɪts/	Ước lượng khoảng
152	Confidence intervals	/ˈkɒnfɪdəns ˈɪntərvəlz/	Khoảng tin cậy
153	Upper limit	/ˈʌpər ˈlɪmɪt/	Giới hạn trên
154	Lower limit	/ˈloʊər ˈlɪmɪt/	Giới hạn dưới
155	Confidence limits	/ˈkɒnfɪdəns ˈlɪmɪts/	Giới hạn tin cậy
156	Null hypothesis	/nʌl haɪˈpɒθəsɪs/	Giả thuyết không
157	Alternative hypothesis	/ɔːlˈtɜːrnətɪv haɪˈpɒθəsɪs/	Giả thuyết thay thế (giả thuyết đối)
158	Pancytopenia	/ˌpænsaɪtoʊˈpiːniə/	Giảm ba dòng tế bào máu
159	Anemia	/əˈniːmiə/	Thiếu máu
160	Neutropenia	/ˌnjuːtrəˈpiːniə/	Giảm bạch cầu trung tính
161	Thrombocytopenia	/ˌθrɒmboʊˌsaɪtoʊˈpiːniə/	Giảm tiểu cầu
162	Acellular	/eɪˈsɛljələr/	Vô bào
163	Hypocellular bone marrow	/ˌhaɪpoʊˈsɛljələr boʊn ˈmæroʊ/	Tủy xương giảm sản
164	Allogeneic bone marrow transplantation	/ˌæloʊdʒəˈniːɪk boʊn ˈmæroʊ ˌtrænsplænˈteɪʃən/	Ghép tủy xương đồng loại
165	Human leukocyte antigen (HLA)	/ˈhjuːmən ˈluːkəˌsaɪt ˈæntɪdʒən/	Kháng nguyên bạch cầu người (HLA)
166	Graft-versus-host disease	/ɡræft ˈvɜːrsəs hoʊst dɪˈziːz/	Bệnh ghép chống chủ
167	Serum titers	/ˈsɪərəm ˈtaɪtərz/	Hiệu giá huyết thanh
168	Cytomegalovirus	/ˌsaɪtoʊˌmɛɡələˈvaɪrəs/	Cytomegalovirus (CMV)
169	Seroconverts	/ˌsɪəroʊkənˈvɜːrts/	Chuyển đổi huyết thanh
170	Seropositive	/ˌsɪəroʊˈpɒzətɪv/	Dương tính huyết thanh
171	Seronegative	/ˌsɪəroʊˈnɛɡətɪv/	Âm tính huyết thanh
172	Skin grafts	/skɪn ɡræfts/	Mảnh ghép da
173	Psoriasis	/səˈraɪəsɪs/	Bệnh vẩy nến
174	Alcohol consumption	/ˈælkəˌhɒl kənˈsʌmpʃən/	Tiêu thụ rượu
175	Case-control study	/keɪs kənˈtroʊl ˈstʌdi/	Nghiên cứu bệnh-chứng
176	Intoxication	/ɪnˌtɒksɪˈkeɪʃən/	Tình trạng say
177	Medical school graduates	/ˈmɛdɪkəl skuːl ˈɡrædʒuɪts/	Sinh viên tốt nghiệp trường y
178	Reproducibility	/ˌriːprəˌduːsəˈbɪləti/	Khả năng tái lập
179	Validity	/vəˈlɪdɪti/	Tính hợp lệ
180	Decision rules	/dɪˈsɪʒən ruːlz/	Các quy tắc quyết định
181	Cardiac risk	/ˈkɑːrdiˌæk rɪsk/	Nguy cơ tim mạch
182	Noncardiac surgery	/nɒnˈkɑːrdiˌæk ˈsɜːrdʒəri/	Phẫu thuật ngoài tim
183	Life expectancy	/laɪf ɪkˈspɛktənsi/	Tuổi thọ kỳ vọng
184	Social determinants of health	/ˈsoʊʃəl dɪˈtɜːrmɪnənts əv hɛlθ/	Các yếu tố xã hội quyết định sức khỏe
185	Self-management	/sɛlf ˈmænɪdʒmənt/	Tự quản lý
186	Chronic diseases	/ˈkrɒnɪk dɪˈziːzɪz/	Bệnh mãn tính
187	Psychosocial variables	/ˌsaɪkoʊˈsoʊʃəl ˈvɛəriəbəlz/	Các biến số tâm lý xã hội
188	Virologically confirmed	/ˌvaɪrəˈlɒdʒɪkli kənˈfɜːrmd/	Được xác nhận bằng virus học
189	Statistical inference	/stəˈtɪstɪkəl ˈɪnfərəns/	Suy luận thống kê
190	Nodal involvement	/ˈnoʊdəl ɪnˈvɒlvmənt/	Sự tham gia của hạch
191	Blood products	/blʌd ˈprɒdʌkts/	Các chế phẩm máu
192	Transfusion	/trænsˈfjuːʒən/	Truyền máu
193	Donor	/ˈdoʊnər/	Người hiến tặng
194	Serum	/ˈsɪərəm/	Huyết thanh
195	Antibodies	/ˈæntiˌbɒdiz/	Kháng thể
196	Transplant	/ˈtrænsˌplænt/	Cấy ghép
197	Cultures of virus	/ˈkʌltʃərz əv ˈvaɪrəs/	Nuôi cấy virus
198	Recreational drug use	/ˌrɛkriˈeɪʃənəl drʌɡ juːs/	Sử dụng ma túy giải trí
199	Controls (in a study)	/kənˈtroʊlz (ɪn ə ˈstʌdi)/	Nhóm chứng (trong một nghiên cứu)
200	pH levels	/piː eɪtʃ ˈlɛvəlz/	Mức độ pH