Thống kê Sinh học Cơ bản và Lâm sàng, Ấn bản thứ 5 – Basic & Clinical Biostatistics, 5e
Tác giả: Susan White – Nhà xuất bản McGraw-Hill Medical – Biên dịch: Ths.Bs. Lê Đình Sáng
Phụ lục B: Đáp án các Bài tập thực hành
Appendix B: Answers to Exercises
CHƯƠNG 2
- Đây là một nghiên cứu thuần tập hồi cứu hoặc nghiên cứu bệnh chứng vì nghiên cứu tận dụng dữ liệu từ một nguồn dữ liệu lịch sử và bao gồm cả nhóm bệnh và nhóm chứng.
- Đây là một nghiên cứu quan sát theo chiều dọc, được phân loại tốt nhất là một nghiên cứu thuần tập. Quần tập ở đây là những bệnh nhân ung thư mới được chẩn đoán.
- Thiết kế nghiên cứu này khá thú vị, và một số người có thể muốn gọi nó là nghiên cứu bệnh chứng. Mục đích là để so sánh liệu pháp tự báo cáo với liệu pháp thực tế. Cả hai thước đo này (tự báo cáo và thực tế) đều xảy ra cùng một thời điểm, do đó nghiên cứu cũng có một số đặc điểm của một nghiên cứu cắt ngang. Theo chúng tôi, nghiên cứu này là bệnh chứng, nhưng nó cho thấy sự khó khăn trong việc phân loại rõ ràng các nghiên cứu vào bất kỳ hệ thống nào.
- Nghiên cứu này là một nghiên cứu quan sát và là một nghiên cứu bệnh chứng bắt cặp.
- Nghiên cứu này là một thử nghiệm lâm sàng ngẫu nhiên có đối chứng với giả dược.
- Nhóm đối tượng đã được xác định và việc thu thập dữ liệu ban đầu diễn ra vào năm 1976; các đối tượng tương tự đã được theo dõi trong những năm tiếp theo. Do đó, thiết kế nghiên cứu này được mô tả tốt nhất là một nghiên cứu thuần tập hoặc nghiên cứu tiền cứu để xác định các yếu tố nguy cơ.
- Có thể có một số thiết kế nghiên cứu, nhưng thực tế nhất là một nghiên cứu quan sát. Một nghiên cứu bệnh chứng cung cấp thông tin nhanh hơn, nhưng cần có một số nghiên cứu bệnh chứng; cần xác định một nhóm ca bệnh cho mỗi nguyên nhân tử vong và loại bệnh tim mạch. Chúng tôi đề nghị bạn sử dụng một trong các chương trình tìm kiếm điện tử để xem bạn có thể tìm thấy một bản sao của một nghiên cứu thuần tập hay không, và nếu có, hãy đọc và thảo luận về những ưu và nhược điểm của cách thức thực hiện nghiên cứu.
CHƯƠNG 3
- Tổng các độ lệch (22.26, 3.36, 15.46, 6.96, … -7.84, -17.04, -0.14) bằng không.
- a. Sử dụng tóm tắt số liệu (Numerical Summary) trong R Commander hoặc chương trình Descriptives trong SPSS, điểm số SF-12 Tổng cộng trung bình cho 1.132 đối tượng là 58.0 với độ lệch chuẩn là 24.8. b. Xem Bảng B-1. c. Xem Hình B-1.
- Tuổi được ghi nhận cho 1.129 bệnh nhân. Tuổi trung bình phải được ước tính bằng công thức trung bình có trọng số. Nó được tìm thấy bằng cách nhân điểm giữa của mỗi khoảng tuổi với số lượng: [ (223 x 55.5) + (366 x 65.5) + (358 x 75.5) + (182 x 85.5) ] / 1129 = 69.92Điểm SF-12 Tổng cộng trung bình được ước tính bằng cách nhân số lượng với giá trị trung bình trong mỗi nhóm tuổi: [ (223 x 61.31) + (366 x 62.76) + (358 x 56.09) + (182 x 47.89) ] / 1129 = 57.96Các giá trị trung bình được tính từ dữ liệu thô là 69.4 tuổi và 57.96. Điểm SF-12 tổng cộng là một ước tính rất tốt vì các giá trị trung bình trong mỗi nhóm tuổi được sử dụng. Tuổi là một ước tính tốt vì bảng này tuân theo các quy tắc xây dựng tần suất tốt bằng cách chọn các giới hạn lớp sao cho hầu hết các quan sát trong lớp gần với điểm giữa của lớp hơn là hai đầu của lớp.
- Xem Bảng B-2. Tỷ số chênh (odds ratio) là (55 x 2847) / (229 x 1438) = 0.476 và cho thấy nguy cơ chẩn đoán cúm được xác nhận cho bệnh nhân có triệu chứng chỉ bằng một nửa trong môi trường bệnh viện nội trú.
- a. Phân phối hai đỉnh (bimodal) với một đỉnh ở độ tuổi 20 và một đỉnh nhỏ hơn ở độ tuổi 40 và 50. b. Lệch dương (skewed positively), với nhiều bác sĩ đỡ khoảng 30-60 ca sinh (bác sĩ gia đình hoặc đa khoa) và ít bác sĩ hơn đỡ 200-250 ca (bác sĩ sản khoa); phân phối cũng có thể là hai đỉnh với một đỉnh ở 50 ca và đỉnh kia ở 225 ca. c. Có lẽ là hình chuông (bell-shaped), với một vài bệnh viện giới thiệu số lượng bệnh nhân rất nhỏ và một vài bệnh viện giới thiệu số lượng rất lớn, nhưng phần lớn giới thiệu số lượng bệnh nhân vừa phải.
- Xem Hình B-2 và Hình B-3.
- a. Mức lương có lẽ không tuân theo đường cong hình chuông; chúng có xu hướng lệch dương, với một vài bác sĩ có mức lương tương đối cao hơn. Do đó, trung vị (median) và khoảng biến thiên (range) hoặc khoảng tứ phân vị (interquartile range) là tốt nhất. b. Các bài kiểm tra năng lực và thành tích được chuẩn hóa được thực hiện trên số lượng lớn người dự thi có xu hướng tuân theo đường cong hình chuông; do đó, trung bình (mean) và độ lệch chuẩn (standard deviation) là phù hợp. c. Giả định phân phối hình chuông là hợp lý, do đó trung bình và độ lệch chuẩn được sử dụng. d. Số lượng khớp đau có lẽ có phân phối lệch dương, do đó trung vị và khoảng biến thiên hoặc khoảng tứ phân vị là phù hợp. e. Sự hiện diện của tiêu chảy hoặc có hoặc không; do đó, đây là một đặc tính danh nghĩa (nominal), và tỷ lệ (proportions) hoặc phần trăm (percentages) là đúng. f. Thang đo thứ tự (ordinal) này đòi hỏi việc sử dụng trung vị và khoảng biến thiên; hoặc có thể sử dụng tỷ lệ hoặc phần trăm. g. Hơi lệch âm, với phần lớn phụ nữ phát bệnh ở độ tuổi 50-70, do đó trung vị và khoảng biến thiên là phù hợp. h. Giả sử sự tuân thủ khá tốt, phân phối có độ lệch dương, với hầu hết bệnh nhân có số lượng thuốc còn lại thấp, và có thể sử dụng trung vị và khoảng biến thiên.
- Tương quan 0.27 thể hiện một mối tương quan dương—khi điểm số kích hoạt (activation score) tăng, điểm số SF-12 tổng cộng cũng tăng. Tương quan -0.19 giữa tuổi và điểm số SF-12 tổng cộng có nghĩa là khi tuổi tăng, điểm số SF-12 tổng cộng giảm.
- a. Khoảng 25 lb, hoặc 11.5 kg. b. Khoảng 18.9 in., hoặc 48 cm. c. Khoảng 16 lb, hoặc 7 kg.
- Hệ số biến thiên (coefficient of variation) của nam giới là 10.84/54.47, hay 19.9%; của nữ giới là 10.71/53.58 hay 20.0%. Do đó, sự biến thiên gần như giống hệt nhau đối với nam và nữ trong mẫu này.
- Tỷ lệ chênh (odds) một người bị đột quỵ lạm dụng ma túy là: (73/214) / (141/214) = 73/141 = 0.518 Tỷ lệ chênh một người không bị đột quỵ lạm dụng ma túy là: (18/214) / (196/214) = 18/196 = 0.092 Do đó, tỷ số chênh (odds ratio) là 0.518/0.092 = 5.64; nghĩa là, một người trong nghiên cứu này lạm dụng ma túy có khả năng bị đột quỵ cao hơn gấp năm lần.
- a. Mục đích của nghiên cứu là tìm hiểu về các tác động cấp tính của acid acetylsalicylic (ASA) lên niêm mạc dạ dày-tá tràng ở nam giới khỏe mạnh trẻ và già. b. Thiết kế nghiên cứu là một thực nghiệm vì có sự can thiệp, và mỗi đối tượng được sử dụng làm đối chứng cho chính mình; do đó, đây là một thử nghiệm lâm sàng tự đối chứng. c. Hai nhóm được sử dụng vì một phần mục đích là để xác định xem có sự khác biệt giữa nam giới trẻ và già hay không. d. Hình 1 trong bài của Moore và cộng sự (1991) cho thấy có mối quan hệ liều-đáp ứng giữa tổng số tổn thương quan sát được qua nội soi: số lượng nhỏ nhất được quan sát trong điều kiện giả dược, và số lượng lớn nhất khi đối tượng nhận 1,300 mg aspirin. Các “râu” dài và các dấu chấm biểu thị các giá trị ngoại lai khi đối tượng nhận 1,300 mg aspirin cho thấy có sự biến thiên đáng kể giữa các đối tượng về tổng số tổn thương quan sát được. e. Hình 2 trong bài của Moore và cộng sự (1991) cho thấy có sự biến thiên đáng kể hơn giữa các đối tượng ở các khoảng giá trị pH cao hơn so với các khoảng thấp hơn. Chú thích hình chỉ ra rằng giá trị trung vị cho ba biểu đồ nằm ở đáy của biểu đồ; điều này có nghĩa là một nửa số nam giới có giá trị pH dưới 1.0.
Bảng B-1. Phân phối tần suất của Điểm SF-12 Tổng cộng.
| Nhóm SF12 | Số lượng | Số lượng Tích lũy | Tỷ lệ phần trăm | Tỷ lệ phần trăm Tích lũy |
|---|---|---|---|---|
| 0-20 | 78 | 78 | 7.2% | 7.29% |
| 21-40 | 251 | 329 | 23.2% | 30.4% |
| 41-60 | 229 | 558 | 21.1% | 51.5% |
| 61-80 | 249 | 807 | 23.0% | 74.5% |
| 81-100 | 276 | 1083 | 25.5% | 100.0% |
(Dữ liệu từ Bos-Touwen I, Schuurmans M, Monninkhof EM, và cộng sự: Các đặc điểm của bệnh nhân và bệnh tật liên quan đến sự kích hoạt tự quản lý ở bệnh nhân đái tháo đường, bệnh phổi tắc nghẽn mạn tính, suy tim mạn tính và bệnh thận mạn tính: một nghiên cứu khảo sát cắt ngang, PLoS One. 2015 May 7;10(5):e0126400.)
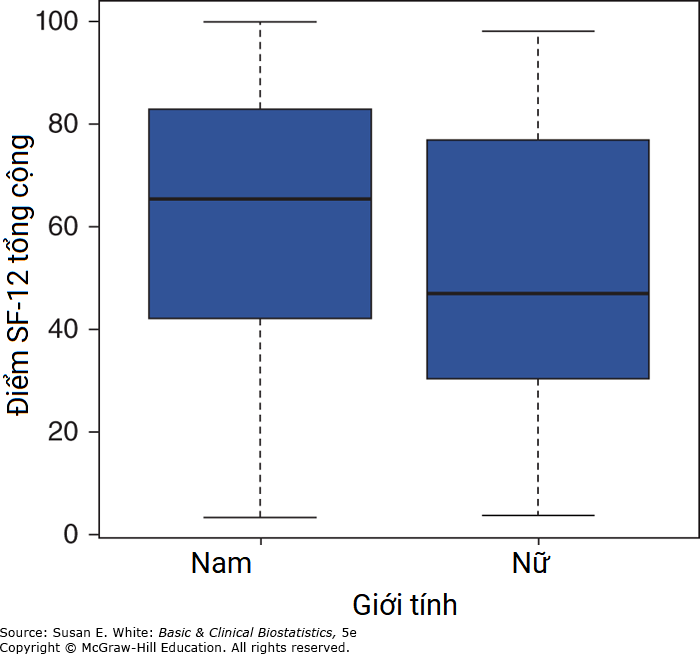
Hình B-1. Biểu đồ hộp về điểm SF-12 tổng cộng cho đối tượng nam và nữ.
Bảng B-2. Bảng ngẫu nhiên cho chẩn đoán cúm và nơi thu thập mẫu và tỷ số chênh.
| Chẩn đoán cúm | |||
|---|---|---|---|
| Nơi thu thập | Có | Không | Tổng |
| Khoa nội trú | 55 | 229 | 284 |
| Khoa ngoại trú | 1438 | 2847 | 4285 |
| Tổng | 1493 | 3076 | 4569 |
(Dữ liệu từ Anderson KB, Simasathien S, Watanaveeradej V, và cộng sự: Các yếu tố dự báo lâm sàng và xét nghiệm về nhiễm cúm ở những người có bệnh giống cúm đến một bệnh viện đô thị ở Thái Lan trong khoảng thời gian năm năm, PLoS One. 2018 Mar 7;13(3):e0193050.)
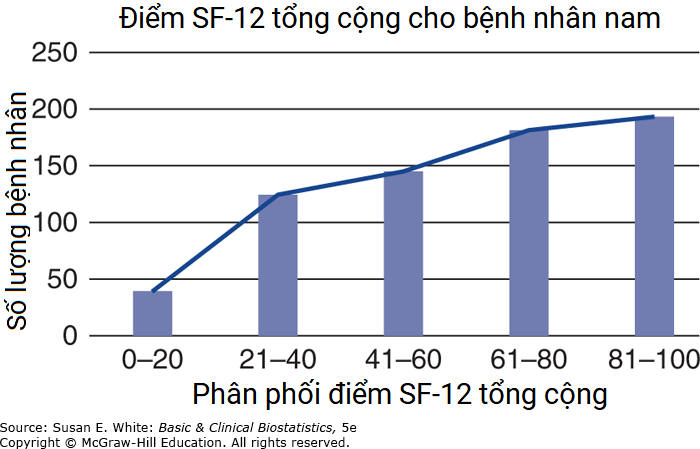
Hình B-2. Phân phối điểm SF-12 tổng cộng cho bệnh nhân nam.
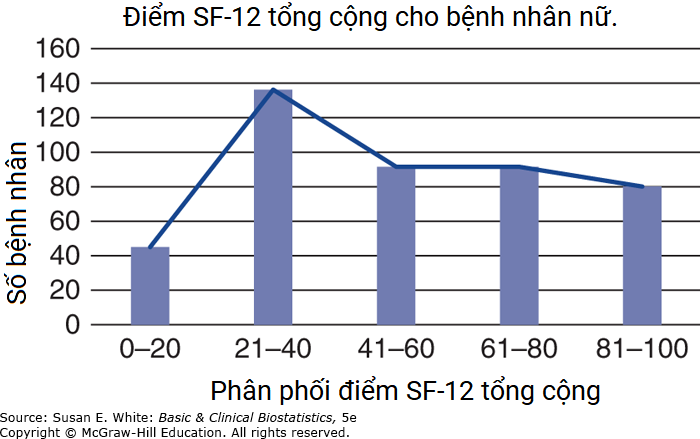
Hình B-3. Phân phối điểm SF-12 tổng cộng cho bệnh nhân nữ.
CHƯƠNG 4
1. a. Để chứng minh rằng giới tính và nhóm máu là độc lập, chúng ta phải chứng minh rằng P(A) x P(B) = P(A và B) cho mỗi ô trong bảng: 0.42 x 0.50 = 0.21 0.43 x 0.50 = 0.215 0.11 x 0.50 = 0.055 0.04 x 0.50 = 0.02
b. P(nam và nhóm máu O) = P(nam | nhóm máu O) x P(nhóm máu O) = (0.21/0.42) x 0.42 = 0.50 x 0.42 = 0.21 Điều này chứng tỏ P(nam | nhóm máu O) = P(nam) khi chúng độc lập.
- Giả sử có 47 bệnh nhân trong nghiên cứu, a. P(mạn tính) = (7+3+2)/47 = 0.29 b. P(cấp tính) = (6+2+2)/47 = 0.21 c. P(cấp tính | chuyển đổi huyết thanh) = 2/18 = 0.11 d. P(chết | dương tính huyết thanh) = 2/8 = 0.25 e. P(âm tính huyết thanh) = 17/47 = 0.36
- Sử dụng phân phối nhị thức, ta có:
, hay 0.20
- a. P(virus cúm A) = 34329/48291 = 0.71 b. P(virus cúm B | 25-64 tuổi) = 4618/16021 = 0.29
- Sử dụng phân phối nhị thức. a. P(nhiễm trùng) = 0.30
, hay 0.20 b. P(sống sót) = 0.80
, hay 0.34
- λ = 1487/390 = 3.81. Xác suất có đúng năm lần nhập viện là
- a. Xác suất một người lớn khỏe mạnh bình thường có natri huyết thanh trên 147 mEq/L là P(z > 2) = 0.023. b. P[z < (130-141)/3] = P(z < -3.67) < 0.001 c. P[(132-141)/3 < z < (150-141)/3] = P(-3 < z < +3) = 0.997 d. 1% trên cùng của phân phối chuẩn hóa được tìm thấy ở z = 2.326; do đó, 2.326 = (X – 141)/3, hay X = 147.98. Vì vậy, mức natri huyết thanh khoảng 148 mEq/L đặt một bệnh nhân vào 1% trên cùng của phân phối. e. 10% dưới cùng của phân phối chuẩn hóa được tìm thấy ở z = -1.28; do đó, -1.28 = (X – 141)/3, hay X = 137.16. Vì vậy, mức natri huyết thanh khoảng 137 mEq/L đặt một bệnh nhân vào 10% dưới cùng của phân phối.
- Phân phối được đưa ra trong Bảng B-3.
Biểu đồ của các phân phối trên cho thấy phân phối nhị thức khá lệch khi tỷ lệ là 0.1 (cũng như khi tỷ lệ gần 1.0, chẳng hạn như 0.9 và 0.8). Khi tỷ lệ gần 0.5, phân phối gần như đối xứng—hoàn toàn đối xứng ở 0.5.
- a. Số tháng trung bình = (12+13+14+15+16)/5 = 14.0 và độ lệch chuẩn là
(Lưu ý rằng độ lệch chuẩn sử dụng 5 trong mẫu số thay vì 4 vì chúng ta giả định rằng 5 quan sát này tạo thành toàn bộ quần thể.)b. Trung bình của các trung bình số tháng = (12+12.5+…+15.5+16)/25 = 14.0 và độ lệch chuẩn của trung bình (hoặc sai số chuẩn của trung bình, SE) là
Lưu ý rằng trung bình của các trung bình tìm thấy trong phần b giống với trung bình tìm thấy trong phần a, và SE giống như
.
- a. Câu hỏi này đề cập đến các cá nhân và tương đương với việc hỏi tỷ lệ diện tích dưới đường cong lớn hơn (103-100)/3 = +1.00 và nhỏ hơn (97-100)/3 = -1.00, sử dụng phân phối z; diện tích là 0.317, hay 31.7%, từ Bảng A-2. b. Câu hỏi này liên quan đến các trung bình. Sai số chuẩn với n=36 là 3/6=0.5. Tỷ số tới hạn cho một trung bình bằng 99 là (99-100)/0.5 = -2.00 và cho 101 là +2.00. Diện tích dưới -2.00 và trên +2.00 là 0.046; do đó, 4.6% các trung bình nằm ngoài giới hạn 99 và 101.
- a. Độ lệch chuẩn là σ = √131(6.2) = 11.45 x 6.2 = 71.0. Khi đó, xác suất một bệnh nhân say rượu hơn 104 lần mỗi năm là P(X>104) = P[z > (104-61.6)/71] = P(z > 0.597). Từ Bảng A-2, P(z>0.60) là 0.274, vì vậy chúng ta biết xác suất này lớn hơn một chút. b. Từ Bảng A-2, giá trị z phân tách 5% trên của phân phối khỏi 95% dưới là 1.645. Chúng ta cần tìm X sao cho
. Giải X cho ra X = (1.645 x 71.0) + 61.6 = 178.4, hay khoảng 179 lần một năm.
- Khoảng 5% sinh viên y khoa tốt nghiệp với khoản nợ 200,000 đô la, và con số này cao hơn 96,000 đô la so với mức trung bình 104,000 đô la. Điểm trong phân phối chuẩn phân tách 5% trên cùng là 1.645. Do đó, 96,000 đô la là 1.645 độ lệch chuẩn; chúng ta chia cho 1.645 để tìm ra một độ lệch chuẩn là 96000 / 1.645 = 58359 đô la.
Bảng B-3. Phân phối nhị thức cho các giá trị khác nhau của tham số, π.
| Xác suất | π = 0.1 | π = 0.3 | π = 0.5 |
|---|---|---|---|
| P(X=0) | 0.531 | 0.118 | 0.016 |
| P(X=1) | 0.354 | 0.303 | 0.094 |
| P(X=2) | 0.098 | 0.324 | 0.234 |
| P(X=3) | 0.015 | 0.185 | 0.313 |
| P(X=4) | 0.001 | 0.060 | 0.234 |
| P(X=5) | <0.001 | 0.010 | 0.094 |
| P(X=6) | <0.001 | 0.001 | 0.016 |
CHƯƠNG 5
1. a. Rộng hơn. b. Tăng kích thước mẫu để có khoảng tin cậy hẹp hơn. c. Hẹp hơn.
- H₀: μ = 0.76 H₁: μ ≠ 0.76 x̄ = 0.68, SE = 0.03 t = (0.68 – 0.76) / 0.03 = -2.667 p-value < 0.01 (với df=14) 95% CI: 0.68 ± (2.145 x 0.03) = 0.68 ± 0.064 hay (0.616, 0.744) Vì giá trị giả thuyết 0.76 không nằm trong khoảng tin cậy 95%, giả thuyết không bị bác bỏ ở mức 0.05. Điều này nhất quán với p-value < 0.01 tìm thấy trong kiểm định giả thuyết.
- Giá trị z hai phía cho α của 0.05 là ±1.96, và giá trị z một phía dưới liên quan đến β=0.80 là khoảng -0.84. Với độ lệch chuẩn là 0.03 và sự khác biệt 0.02 m, kích thước mẫu là khoảng 18. Con số này nhỏ hơn nhiều so với mẫu cần thiết để tìm ra sự khác biệt 0.01 m.
hay 71.
- Chúng tôi đã tìm thấy kích thước mẫu cần thiết là 408 để phát hiện sự khác biệt giữa 17% và 12%. Để có công suất 80% để tìm ra sự khác biệt giữa 17% và 10%, một mẫu 200 là đủ. Kích thước mẫu nhỏ hơn là cần thiết khi sự khác biệt chúng ta muốn phát hiện lớn hơn.
hay 200.
- Các tính toán công suất của chúng tôi giả định SD=0.03, và Rabago và cộng sự (2015) có SD là 0.04. Điều này minh họa vai trò của độ lệch chuẩn trong việc tìm kiếm kích thước mẫu.
- Giải X: t = (x̄ – 1.7) / (1.7/√10) > 2.179 x̄ / 0.538 > 2.179 x̄ > 1.17
- Xem Bảng B-4. Họ đồng ý một cách tình cờ rằng (30/50) x (35/50) = 60% x 70% hay 42% là âm tính và 40% x 30% hay 12% là dương tính, tổng cộng là 54% các phim chụp X-quang tuyến vú. Họ thực sự đồng ý trên 25+10 hay 35 trên 50, tức 70%. κ = (Sự đồng thuận quan sát được – Sự đồng thuận kỳ vọng) / (1 – Sự đồng thuận kỳ vọng) κ = (0.70 – 0.54) / (1 – 0.54) = 0.16 / 0.46 = 0.348
- a. Biểu đồ tần suất của sự thay đổi điểm số M-wave trong Hình B-4 cho thấy một phân phối lệch. Nên sử dụng kiểm định Wilcoxon. b. Cả kiểm định Wilcoxon và kiểm định t cặp đều cho cùng một kết luận—không bác bỏ giả thuyết không rằng sự khác biệt bằng 0.
- a. Phân phối độ rộng sải chân của nam giới bị lệch về bên phải (xem Hình B-5). Do đó, nên sử dụng một thủ tục phi tham số. b. Kiểm định dấu một mẫu: s = 0, p-value = 0.00006104 Giả thuyết thay thế: trung vị thực sự không bằng 0.15 Khoảng tin cậy 95%: 0.08189084 đến 0.10500000 Ước tính mẫu: trung vị của x = 0.104 Kiểm định t một mẫu: t = -9.6922, df = 14, p-value = 0.0000001374 Giả thuyết thay thế: trung bình thực sự không bằng 0.15 Khoảng tin cậy 95%: 0.08592302 đến 0.10914364 Ước tính mẫu: trung bình của x = 0.09753333 Cả hai kiểm định đều cho cùng một kết luận—bác bỏ giả thuyết không với p < 0.0001.
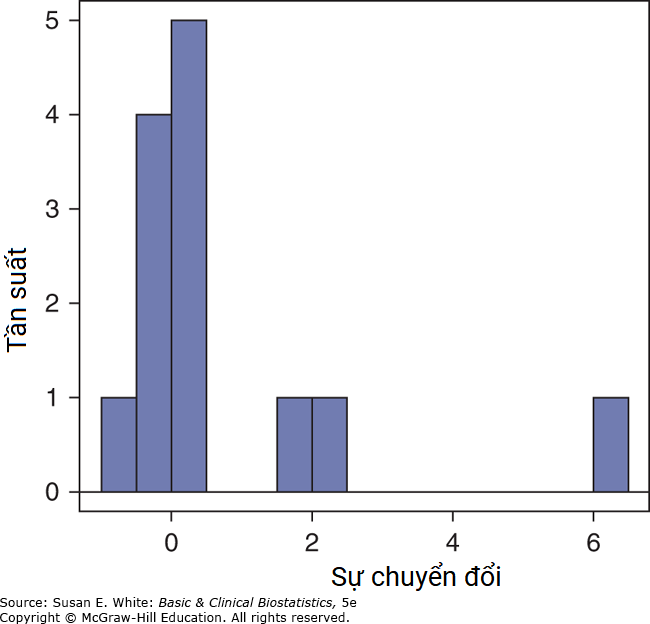
Hình B-4. Biểu đồ tần suất về sự thay đổi điểm số M-wave.
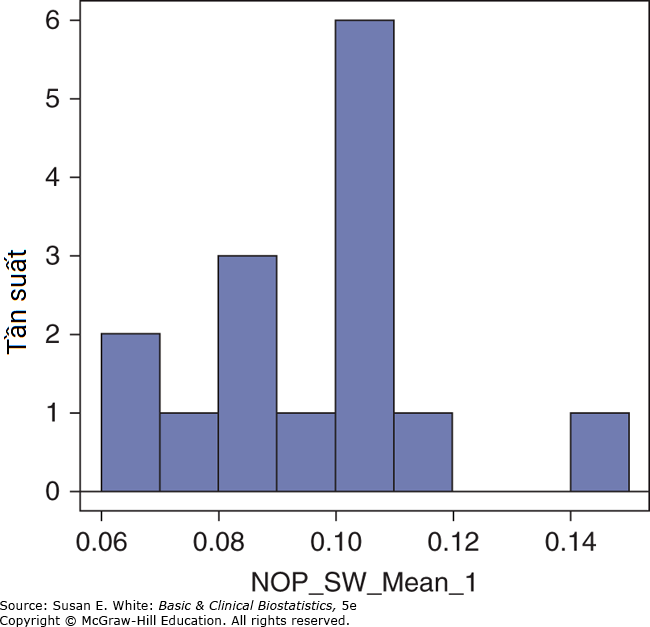
Hình B-5. Độ rộng sải chân của nam giới không có nhiễu loạn.
Bảng B-4. Phân loại một mẫu gồm 50 phim chụp nhũ ảnh bởi hai bác sĩ.
| Bác sĩ 1 | Bác sĩ 2 | |
|---|---|---|
| Âm tính | Dương tính | |
| Âm tính | 25 | 5 |
| Dương tính | 10 | 10 |
| Tổng | 35 | 15 |
CHƯƠNG 6
- Giá trị tới hạn của t là như nhau, 1.96 nếu sử dụng nội suy, và độ lệch chuẩn gộp và sai số chuẩn phải được tính lại. Khoảng tin cậy 95% là:
1.9 ± 1.96 x 2.16 1.9 ± 4.23 -2.33 đến 6.13 Khoảng tin cậy này rộng hơn so với khoảng tin cậy trong phần “Quyết định về Trung bình trong hai nhóm độc lập” và bây giờ chứa số không. Do đó, chúng ta sẽ kết luận rằng không có sự khác biệt về đo oxy xung nếu chỉ có 50 bệnh nhân trong mỗi nhóm.
- Nếu kích thước mẫu bằng nhau, n₁ = n₂, vì vậy chúng ta có thể chỉ cần sử dụng n trong công thức cho SD gộp. Kết quả là SD gộp là căn bậc hai của trung bình của SD₁² và SD₂²:
- Giả thuyết không là điểm PAM là như nhau, và giả thuyết thay thế là chúng không giống nhau. Kiểm định t có thể được sử dụng cho câu hỏi nghiên cứu này; chúng ta sử dụng α là 0.05 để có thể so sánh kết quả với khoảng tin cậy 95%. Bậc tự do là 422+732-2 = 1152 nên giá trị tới hạn là 1.96. Độ lệch chuẩn gộp được tính trước đó trong Chương 6 là 10.75. Vì vậy, thống kê t là:
t = 2.87 và lớn hơn giá trị tới hạn 1.96, vì vậy chúng ta bác bỏ giả thuyết không và kết luận rằng, trung bình, bệnh nhân mắc CRD có điểm PAM cao hơn so với bệnh nhân không mắc CRD.
- Gọi N là tổng số quan sát, A là số quan sát trong một hàng đã cho, và K là số quan sát trong một cột đã cho. Ví dụ, đối với một bảng có hai hàng và ba cột, chúng ta có Bảng B-5, trong đó chúng ta muốn tìm giá trị kỳ vọng cho ô có dấu hoa thị (*). Xác suất một quan sát xảy ra ở hàng A, P(A), là A/N, và xác suất một quan sát xảy ra ở cột K, P(K), là K/N. Giả thuyết không được kiểm định bởi khi-bình phương là các sự kiện được biểu thị bởi các hàng và cột là độc lập. Sử dụng quy tắc nhân cho các sự kiện độc lập, xác suất một quan sát xảy ra ở hàng A và cột K là P(A)P(K) = (A/N) x (K/N) = AK/N². Nhân xác suất này với tổng số quan sát N cho ra số quan sát xảy ra ở cả hàng A và cột K; tức là, (AK/N²) x N = AK/N, hay (tổng hàng x tổng cột) / tổng chung.
- Quy tắc ngón tay cái cho α bằng 0.05 và công suất bằng 0.80 có zα = 1.96 và zβ = -1.28 cho tất cả các tính toán; tức là, chỉ có σ và (μ₀ – μ₁) thay đổi. Do đó,
- Kết quả từ G*Power (Hình B-6) cho thấy cần 20 bệnh nhân để có công suất 80%.
- Khoảng tin cậy 95%, đã được thảo luận trước đó trong Chương 6, là -1.9 ± (1.96)(0.66) = 1.9 ± 1.29, hay 0.61 đến 3.28. Để có khoảng tin cậy 90% và 99%, chỉ cần thay đổi giá trị t với 919 bậc tự do. Khoảng tin cậy 90% là -1.9 ± (1.645)(0.66) = 1.9 ± 1.08 hay 0.81 đến 2.99. Khoảng tin cậy 99% là -1.9 ± (2.576)(0.66) = 1.9 ± 1.70 hay 0.20 đến 3.60. Độ tin cậy thấp hơn cho một khoảng hẹp hơn, và độ tin cậy cao hơn đòi hỏi một khoảng rộng hơn.
- Có khả năng cao là có nhiều sự biến thiên hơn về số lượng thủ thuật được thực hiện ở các trung tâm cỡ vừa. Kiểm định t yêu cầu phương sai (hoặc độ lệch chuẩn) không khác nhau ở hai nhóm. Vì kích thước mẫu khá khác nhau, 60 so với 25, có thể việc vi phạm giả định về phương sai bằng nhau đã dẫn đến một kiểm định t không có ý nghĩa thống kê.
Bảng B-5. Bảng ngẫu nhiên với hai hàng và ba cột.
| Cột J | Cột K | Cột L | Tổng | |
|---|---|---|---|---|
| Hàng A | * | A | ||
| Hàng B | B | |||
| Tổng | J | K | L | N |
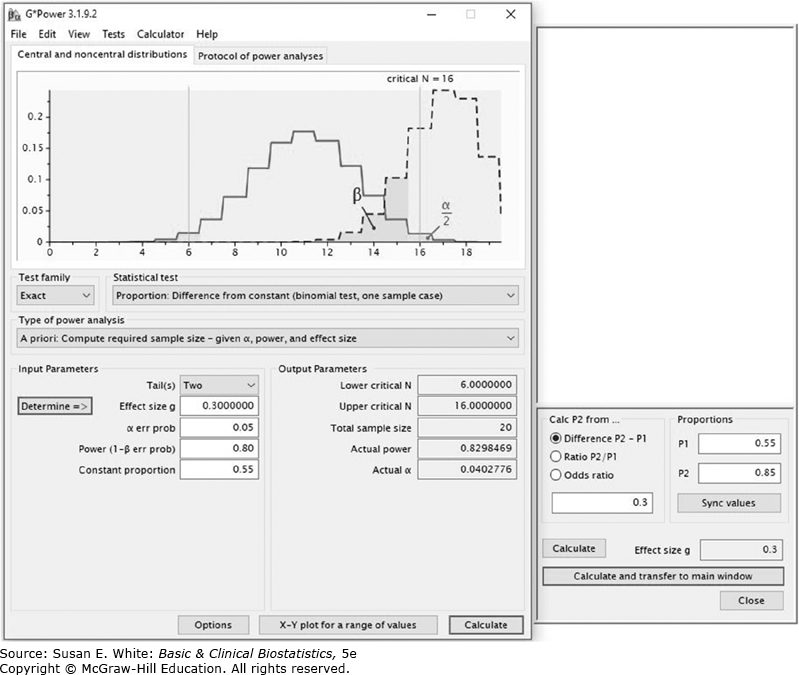
Hình B-6. Kích thước mẫu để phát hiện sự khác biệt về tỷ lệ.
CHƯƠNG 7
- Kết quả ANOVA được đưa ra trong Bảng B-6. Giá trị quan sát được cho tỷ số F là 11.09, với 2 và 107 bậc tự do. Giá trị tới hạn từ Bảng A-4 với 2 và 70 bậc tự do (giá trị gần nhất) là khoảng 3.14 tại p=0.05; do đó, có đủ bằng chứng để kết luận rằng mức ADMA trung bình không giống nhau cho cả ba nhóm bệnh nhân.
- Tham khảo Bảng B-6; các thủ tục Tukey và Scheffé chỉ ra rằng nhóm HIV+ART+ khác với cả hai nhóm HIV- và HIV+ART-.
- Hai so sánh là độc lập nếu chúng sử dụng thông tin không chồng chéo. a. Độc lập vì mỗi so sánh sử dụng dữ liệu khác nhau. b. Phụ thuộc vì dữ liệu về bác sĩ được sử dụng trong mỗi so sánh. c. Độc lập vì mỗi so sánh sử dụng dữ liệu khác nhau. d. Không có so sánh nào trong ba so sánh này là độc lập với hai so sánh còn lại vì tất cả chúng đều sử dụng dữ liệu về sinh viên y khoa.
- a. Đây là ANOVA một yếu tố (one-way), vì chỉ có một thành phần không phải sai số, đó là thành phần giữa các nhóm. b. Tổng biến thiên là 2.000. c. Có bốn nhóm bệnh nhân vì bậc tự do là 3. Có 40 bệnh nhân vì n-4=36. d. Tỷ số F là (800/3)/33.3 = 8.01. e. Giá trị tới hạn với 3 và 30 bậc tự do là 4.51; với 3 và 40 bậc tự do là 4.31; nội suy cho 3 và 36 bậc tự do cho ra 4.39. f. Bác bỏ giả thuyết không về không có sự khác biệt và kết luận rằng huyết áp trung bình khác nhau ở các nhóm tiêu thụ lượng rượu khác nhau. Cần có một so sánh hậu kiểm (post hoc) để xác định cụ thể nhóm nào trong bốn nhóm khác nhau.
- a. Không, giá trị p là 0.545. b. Có, giá trị p là 8.49 x 10⁻⁶ hay 0.00000849. c. Có, tương tác cũng có ý nghĩa thống kê, với p=0.00000580. d. Một tương tác có ý nghĩa thống kê có nghĩa là ảnh hưởng của một trong các yếu tố, chẳng hạn như loại bệnh vẩy nến, phụ thuộc vào mức độ của yếu tố kia, tuổi khởi phát. Do đó, không thể rút ra bất kỳ kết luận nào về các yếu tố một cách độc lập; chúng ta không thể nói đơn giản rằng %TBSA khác nhau theo loại di truyền so với loại ngẫu nhiên; chúng ta phải lưu ý rằng sự khác biệt phụ thuộc vào tuổi khởi phát.
Bảng B-6. ANOVA của ADMA theo Nhóm HIV
|
Nguồn biến thiên |
df | Tổng bình phương | Trung bình bình phương | Giá trị F | Pr(>F) |
|---|---|---|---|---|---|
| Nhóm | 2 | 0.3962 | 0.19811 | 11.09 | 0.0000419 |
| Sai số | 107 | 1.9110 | 0.01786 |
Mức ý nghĩa: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1
So sánh bội các Trung bình: Tương phản Tukey
| Tương phản | Ước tính | Lỗi chuẩn | Giá trị t | Pr(>|t|) |
|---|---|---|---|---|
| HIV+ART- – HIV- | 0.02803 | 0.02960 | 0.947 | 0.61114 |
| HIV+ART+ – HIV- | -0.11992 | 0.03328 | -3.603 | 0.00138 ** |
| HIV+ART+ – HIV+ART- | -0.14795 | 0.03231 | -4.580 | < 0.0001 *** |
CHƯƠNG 8
1. a.
b. ``
Khoảng tin cậy 95%:
``
(1.26, 1.49)
Vì khoảng tin cậy không chứa 1, do đó, có đủ bằng chứng để kết luận rằng tồn tại nguy cơ mắc bệnh Alzheimer có ý nghĩa thống kê ở những đối tượng dùng benzodiazepine.
- a. Bệnh chứng. b. Tỷ số chênh là (20 x 1,157) / (41 x 121) = 4.66; khoảng tin cậy 95% là antilog của
- a và b. Các giải pháp được tính toán bằng R cho phần a và b ở dưới đây. Tương quan moment sản phẩm Pearson dữ liệu: Tổng điểm IPQ và tổng điểm SF12 t = -10.276, df = 177, p-value < 2.2e-16 Giả thuyết thay thế: tương quan thực sự không bằng 0 Khoảng tin cậy 95 phần trăm: -0.6955788 đến -0.5103537 Ước tính mẫu: cor = -0.6112695
- a. BMI có mối quan hệ mạnh nhất với tuổi. b. BMI, vì nó có tương quan cao nhất.
- Đường hồi quy đi qua điểm (X̄, Ȳ); do đó, điểm mà X̄ giao với đường hồi quy, khi chiếu lên trục Y, là Y’ = Ȳ.
- a. Các câu hỏi được nghiên cứu giải quyết là: Sinh bệnh học của hội chứng thận hư đáp ứng steroid (SRNS) có phải qua trung gian phức hợp miễn dịch không? Hoạt động lâm sàng của bệnh có liên quan đến sự hiện diện của các phức hợp miễn dịch lưu hành không? b. Các nhóm có sẵn đã được sử dụng, bệnh nhân SRNS và bệnh nhân lupus ban đỏ hệ thống (SLE), vì vậy nghiên cứu không được ngẫu nhiên hóa. Không có điều trị nào được thực hiện, vì vậy nó không phải là một thử nghiệm lâm sàng. Các quan sát về các biến quan tâm, các phức hợp chứa IgG và sự gắn kết C1q, được thu thập cùng một lúc, và câu hỏi nghiên cứu tập trung vào “Điều gì đang xảy ra?” Do đó, nghiên cứu này được mô tả tốt nhất là cắt ngang. c. Bệnh nhân có và không có bằng chứng về bệnh đang hoạt động đã được nghiên cứu. Bệnh nhân SLE cũng được nghiên cứu vì các phức hợp miễn dịch được biết là có vai trò gây bệnh trong bệnh này. d. Theo Hình 8-21, tương quan giữa gắn kết C1q và các phức hợp IgG đối với bệnh nhân SLE là có ý nghĩa thống kê, r=0.91, nhưng kết quả này tự nó không thiết lập mối quan hệ nhân quả. Tương quan không có ý nghĩa thống kê đối với bệnh nhân SRNS, nhưng kích thước mẫu tương đối nhỏ, cho thấy công suất thấp để phát hiện một mối quan hệ có ý nghĩa. e. Các tác giả nói rằng các đường này là giới hạn tin cậy 95% cho các bệnh nhân lupus. Tuy nhiên, các đường này song song, thay vì cong, như chúng phải vậy. Chúng có thể liên quan đến các cá nhân, bởi vì (1) cách chúng được mô tả trong chú thích, và (2) giới hạn cho trung bình có lẽ sẽ gần đường hồi quy hơn. f. Không thể nói chắc chắn; tuy nhiên, có vẻ như chúng có thể khác nhau. Thứ nhất, tương quan đối với bệnh nhân SRNS không khác biệt đáng kể so với 0 và tương quan đối với bệnh nhân SLE là 0.91; nếu các tương quan khác nhau, thì các đường hồi quy cũng vậy. Tuy nhiên, kích thước mẫu của bệnh nhân SRNS rất nhỏ và có thể ngăn chúng ta phát hiện ra sự khác biệt có ý nghĩa thống kê. g. Không. Quần thể nghiên cứu phải được xác định cẩn thận để giảm khả năng bao gồm các bệnh nhân có các quá trình bệnh khác.
CHƯƠNG 9
1. a. Xem Bảng B-7 để biết sự sắp xếp các quan sát theo thời gian bệnh nhân tham gia nghiên cứu và xác suất sống sót. b. Đường cong sống còn, được tạo bằng R, được đưa ra trong Hình B-7. c. Thông tin cho thống kê log-rank được hiển thị trong Bảng B-8.
2. a. Các đường cong sống còn được đưa ra trong Hình B-8. Có vẻ như tỷ lệ sống sót của các đối tượng có nồng độ MMP-14 huyết thanh cao (đường đứt nét trong hình) có thời gian sống ngắn hơn. Điều này nhất quán trong suốt khoảng thời gian. b. Thống kê log-rank là 10.2 (sử dụng hàm survdiff trong R). Vì đây là một thống kê khi-bình phương với 1 bậc tự do, chúng ta biết rằng giá trị này cho thấy ý nghĩa thống kê (p=0.001). Do đó, chúng tôi kết luận rằng những quan sát này cung cấp đủ bằng chứng về sự khác biệt trong sự sống còn ở hai nhóm MMP-14 huyết thanh. c. Nghiên cứu này là quan sát và không được ngẫu nhiên hóa. Do đó, sự khác biệt được tìm thấy có thể là do các đồng biến khác có thể ảnh hưởng đến sự sống còn và/hoặc mức MMP-14.
- Các bệnh nhân điều trị kết hợp có thời gian sống trung vị khoảng 15 tháng. Những người chỉ được điều trị bằng regorafenib có thời gian sống trung vị là 10 tháng.
- a. Các đường cong Kaplan-Meier được đưa ra trong Hình B-9. b. Các đường cong được phân tách rộng rãi, cho thấy sự khác biệt lớn đối với những người được phân loại là khối u loại ruột so với loại lan tỏa. Biến phân loại dường như là một chỉ số hợp lệ về nguy cơ và nên được đưa vào như một đồng biến trong phân tích.
- Thủ tục Mantel-Haenszel là một thủ tục tuyệt vời để so sánh hai phân phối. Lưu ý rằng có thể ước tính thống kê Mantel-Haenszel từ Hình B-2 của nghiên cứu.
- a. Sự sống còn tốt nhất đối với bệnh nhân có bệnh giới hạn ở một mạch máu duy nhất. b. Tỷ lệ tử vong cao nhất được quan sát thấy ở những bệnh nhân bị bệnh thân chung động mạch vành trái hoặc bệnh ba thân mạch vành. c. Thời gian sống trung vị cho nhóm bị bệnh một thân mạch vành là khoảng 18 năm; đối với hai nhóm còn lại là khoảng 12 năm.
Bảng B-7. Bảng Kaplan-Meier cho bệnh nhân ghép thận.
| Điều trị = azathioprine | Điều trị = cyclosporine | ||||||
| Thứ hạng | Cỡ mẫu | Thời gian | Sống sót S(t) | Thứ hạng | Cỡ mẫu | Thời gian | Sống sót S(t) |
| 1 | 31 | 1.0 | 0.967742 | 1 | 21 | 1.0 | 0.952381 |
| 2 | 30 | 1.0 | 0.935484 | 2 | 20 | 6.0 | 0.904762 |
| 3 | 29 | 1.0 | 0.903226 | 3 | 19 | 8.0 | 0.857143 |
| 4 | 28 | 1.0+ | 4 | 18 | 12.0+ | ||
| 5 | 27 | 1.0+ | 5 | 17 | 12.0+ | ||
| 6 | 26 | 2.0 | 0.868486 | 6 | 16 | 12.0+ | |
| 7 | 25 | 2.0+ | 7 | 15 | 13.0+ | ||
| 8 | 24 | 3.0 | 0.832299 | 8 | 14 | 14.0+ | |
| 9 | 23 | 3.0 | 0.796112 | 9 | 13 | 15.0+ | |
| 10 | 22 | 3.0 | 0.759926 | 10 | 12 | 15.0+ | |
| 11 | 21 | 4.0+ | 11 | 11 | 16.0+ | ||
| 12 | 20 | 5.0 | 0.721929 | 12 | 10 | 17.0+ | |
| 13 | 19 | 5.0+ | 13 | 9 | 17.0+ | ||
| 14 | 18 | 5.0+ | 14 | 8 | 18.0+ | ||
| 15 | 17 | 8.0+ | 15 | 7 | 19.0+ | ||
| 16 | 16 | 8.0+ | 16 | 6 | 19.0+ | ||
| 17 | 15 | 8.0+ | 17 | 5 | 20.0+ | ||
| 18 | 14 | 10.0+ | 18 | 4 | 21.0+ | ||
| 19 | 13 | 10.0+ | 19 | 3 | 22.0+ | ||
| 20 | 12 | 12.0+ | 20 | 2 | 22.0+ | ||
| 21 | 11 | 12.0+ | 21 | 1 | 22.0+ | ||
| 22 | 10 | 13.0+ | |||||
| 23 | 9 | 14.0+ | |||||
| 24 | 8 | 15.0+ | |||||
| 25 | 7 | 17.0 | 0.618797 | ||||
| 26 | 6 | 18.0+ | |||||
| 27 | 5 | 18.0+ | |||||
| 28 | 4 | 19.0+ | |||||
| 29 | 3 | 20.0+ | |||||
| 30 | 2 | 23.0+ | |||||
| 31 | 1 | 23.0+ | |||||
Data from Dr. Alan Birtch.
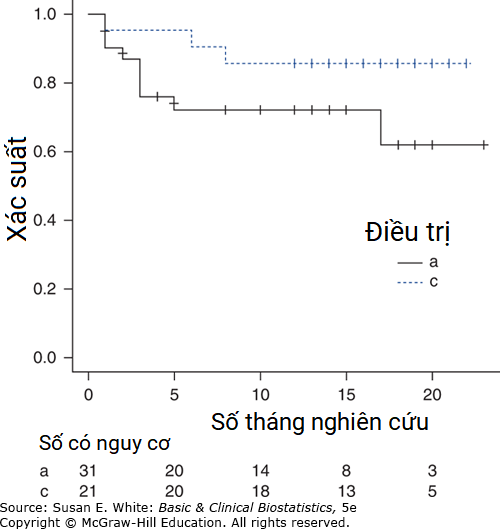
Hình B-7. Đường cong sống sót cho bệnh nhân ghép thận.
Bảng B-8. Thông tin về thống kê logrank.
| Giá trị điều trị |
Số ca thất bại |
Số ca kiểm duyệt | Tổng số |
|---|---|---|---|
| Azathioprine | 9 | 22 | 31 |
| Cyclosporine | 3 | 18 | 21 |
| Khi-bình phương = 2.38 | df = 1 |
p = 0.12 |
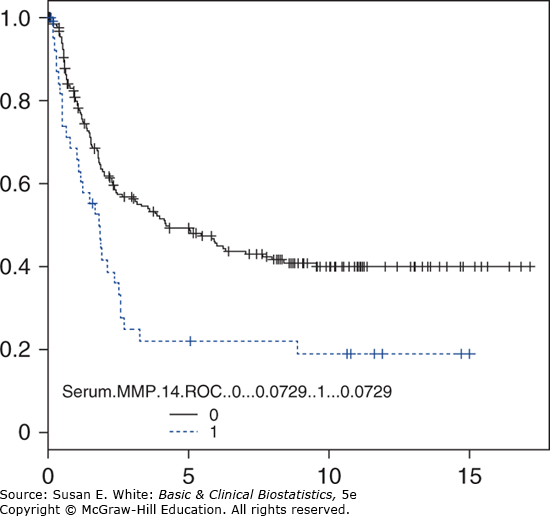
Hình B-8. Đường cong sống sót cho bệnh nhân có MMP-14 cao so với thấp.
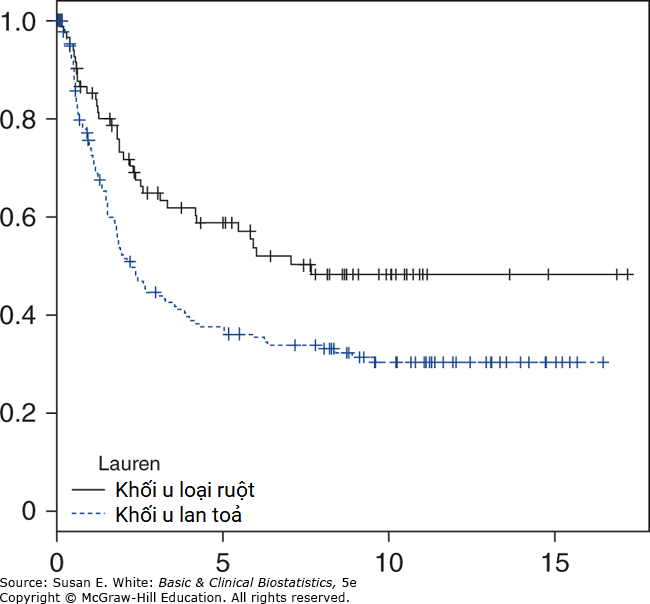
Hình B-9. Đường cong sống sót Kaplan-Meier theo phân loại Lauren.
CHƯƠNG 10
- Đối với người hút thuốc, trung bình đã điều chỉnh là trung bình ở người hút thuốc, 3.33, trừ đi tích của hệ số hồi quy, 0.0113, và sự khác biệt giữa điểm tắc nghẽn ở người hút thuốc và điểm tắc nghẽn trong toàn bộ mẫu (ước tính từ Hình 10-3); tức là, 3.33 – 0.0113 x (198.33 – 151.67) = 2.80 Tương tự, trung bình đã điều chỉnh ở người không hút thuốc là 1.00 – 0.0113 x (105.00 – 151.67) = 1.53 Đây là những giá trị tương tự mà chúng tôi đã tìm thấy (trong sai số làm tròn) trong phần “Kiểm soát yếu tố gây nhiễu”.
- Giá trị dự đoán cho một bệnh nhân có ASA=1, tình trạng chức năng kém, tăng huyết áp nặng đang trải qua một phẫu thuật mở kéo dài 1.5 giờ: -3.246 + 0.887 x [ASA>3] + 0.754 x [tình trạng chức năng kém] + 0.632 x [Không có THA] + 1.084 x [phương pháp mở] + 0.838 x [dài hơn 2 giờ] và chúng ta đánh giá nó như sau: -3.246 + 0.887x[0] + 0.754x[1] + 0.632x[0] + 1.084x[1] + 0.838x[0] = -1.408 và
- Xem Bảng B-9
- Nếu các nhà điều tra muốn phân biệt giữa ba nhóm người chạy, sử dụng các thước đo nhân trắc học số, nên sử dụng phân tích phân biệt. Tuy nhiên, có thể sử dụng hồi quy bội, nếu thời gian chạy thực tế của mỗi người chạy được sử dụng thay vì chia người chạy thành ba nhóm; trong tình huống này, thước đo kết cục là số.
- Biết bệnh nhân là phụ nữ và trong chương trình trả lương FFS, phương trình hồi quy là 0.613 – [0.26 x 0(nếu là nam)] – [0.014 x 1(nếu trong FFS)] – [0.0002 x 80(chức năng cá nhân)] – [0.00006 x 80(sức khỏe tâm thần)] – [0.002 x 75(nhận thức sức khỏe)] – [0.0001 x 70(tuổi)] – [0.021 x 10(giá trị thang thu nhập)] + [0.002 x 1(nếu kỳ hạn 3 năm)] – [0.003 x 1(nếu đã khám sức khỏe)] + [0.105 x 14(số ngày nằm giường tại thời điểm 0)] = 0.613 – 0.014 – 0.016 – 0.0048 – 0.150 – 0.007 – 0.210 + 0.002 – 0.003 + 1.470 = 1.680 cho ra 1.68 ngày nằm giường dự đoán trong khoảng thời gian 30 ngày.
- a. Hệ số hồi quy là -0.267, cho thấy mối quan hệ âm. b. Hệ số hồi quy âm cho thấy tuổi cao hơn có liên quan đến điểm trầm cảm thấp hơn, cho thấy ít trầm cảm hơn. Nó không có ý nghĩa thống kê vì giá trị p là 0.538. Một cách giải thích có thể là mọi người có xu hướng có khả năng đối phó tốt hơn với các tình trạng thể chất và hoàn cảnh xảy ra khi tuổi tác tăng lên, nhưng đây hoàn toàn là suy đoán. c. Khối về sức khỏe thể chất làm tăng
- a. Kết quả hồi quy của bạn nên giống với kết quả chúng tôi đã tạo ra trong Bảng 10-13. b. Chiều cao của cha là biến được đưa vào mô hình 1. Hồi quy từng bước bắt đầu với biến độc lập có tương quan cao nhất với kết cục, vì vậy chiều cao của cha có tương quan cao nhất với chiều cao cuối cùng của trẻ. c. Chiều cao của mẹ, chiều cao theo tuổi thời gian, và liều lượng nằm trong mô hình cuối cùng. Dựa trên các hệ số chuẩn hóa, biến đóng góp lớn nhất là chiều cao theo tuổi thời gian. d. Sau khi các biến khác được đưa vào phương trình trong mô hình 4, chiều cao của cha không còn có ý nghĩa thống kê. Điều này có thể xảy ra khi các biến khác đang dự đoán cùng một phần của kết cục mà chiều cao của cha đã dự đoán, một khi giá trị của tất cả các biến khác được giữ không đổi. e. -1.138 + (-0.575 x -2.20) + (1.325 x -3.07) + (0.121 x 20) = -1.138 + 1.265 – 4.068 + 2.42 = -1.52 Do đó, chiều cao cuối cùng của đứa trẻ này được dự đoán là -1.52, so với chiều cao thực tế của đứa trẻ là -2.18.
Bảng B-9. Tính toán Hệ số Kappa.
| Quan sát | Dự đoán | |||
|---|---|---|---|---|
| LOS>7 ĐÚNG | LOS>7 SAI | Tổng | ||
| LOS>7 ĐÚNG | 409 | 22 | 431 | |
| LOS>7 SAI | 90 | 26 | 116 | |
| Tổng | 499 | 48 | 547 | |
| Kỳ vọng | Dự đoán | |||
| LOS>7 ĐÚNG | LOS>7 SAI | Tổng | ||
| LOS>7 ĐÚNG | 393.18 | 37.82 | 431 | |
| LOS>7 SAI | 105.82 | 10.18 | 116 | |
| Tổng | 499 | 48 | 547 | |
| Đồng ý kỳ vọng | 0.7374 | |||
| Đồng ý quan sát | 0.7952 | |||
| Kappa | 0.2203 |
|
CHƯƠNG 11
1. a. Một nhóm không đại diện; những người không thích hãng hàng không có lẽ không có mặt trên máy bay; chuyến bay chưa kết thúc. b. Sai lệch đáp ứng; chỉ những người có quan điểm mạnh mẽ theo một hướng nào đó có xu hướng trả lời. c. Thông thường, các bảng câu hỏi về sự hài lòng của bệnh nhân có tính chất rất chung chung và cung cấp ít chi tiết về các vấn đề thực tế; tỷ lệ phản hồi rất thấp, thường dưới 10%. Có thể tốt hơn nếu tập trung nguồn lực vào các bảng câu hỏi về các chủ đề cụ thể được gửi đến các mẫu ngẫu nhiên của bệnh nhân với sự theo dõi đầy đủ để tạo ra một tỷ lệ phản hồi đáng tin cậy. d. Sinh viên có thể sợ rằng câu trả lời của họ sẽ bị nhận dạng theo một cách nào đó và có thể do dự thể hiện cảm xúc thật của mình.
- Tùy thuộc vào câu hỏi bạn muốn trả lời, bạn có thể hình thành các khoảng tin cậy cho các trung bình hoặc kiểm tra các tương quan giữa các câu trả lời cho các biến khác nhau.
- Có thể dễ dàng hơn cho cha mẹ ước tính số giờ con họ xem TV trong một tuần trung bình thay vì một tháng. Hoặc, bác sĩ nhi khoa có thể liệt kê một bộ các lựa chọn, chẳng hạn như 0-5, 6-10, 10-15, v.v.
- Cả hai mặt của vấn đề nên được trình bày trong một câu hỏi để tránh định hướng người trả lời. Sẽ tốt hơn nếu hỏi: “Bạn đồng ý hay không đồng ý rằng giờ làm việc mới của phòng khám là một sự cải tiến so với giờ làm việc cũ?” Tốt hơn nữa là: “Ý kiến của bạn về giờ làm việc mới của phòng khám so với giờ làm việc cũ là gì?” và cung cấp năm câu trả lời như: tốt hơn nhiều, tốt hơn một chút, không khác biệt, tệ hơn một chút, tệ hơn nhiều.
- Hoặc d hoặc e, tùy thuộc vào lượng tài nguyên bạn có để thu thập danh sách thành viên.
CHƯƠNG 12
1. a. Với tỷ lệ ban đầu là 2% và độ nhạy 95%, 0.95 x 20 = 19 dương tính thật; với độ đặc hiệu 50%, tỷ lệ dương tính giả là 50% và 0.50 x 980 = 490 dương tính giả xảy ra. Xác suất bị lupus với một xét nghiệm dương tính là
- Sử dụng định lý Bayes với D = lupus và T = xét nghiệm, chúng ta có:
- Sử dụng phương pháp tỷ số khả dĩ đòi hỏi chúng ta phải định nghĩa lại tỷ lệ chênh trước xét nghiệm là tỷ lệ chênh của việc không mắc bệnh, tức là, 0.98/(1-0.98) = 49. Tỷ số khả dĩ cho một xét nghiệm âm tính là độ đặc hiệu chia cho tỷ lệ âm tính giả (tức là, khả năng có xét nghiệm âm tính ở người không mắc bệnh so với người mắc bệnh); do đó, tỷ số khả dĩ là 0.50/0.05 = 10. Nhân lên, chúng ta được 49 x 10 = 490, tỷ lệ chênh sau xét nghiệm. Chuyển đổi lại thành xác suất sau xét nghiệm, hoặc giá trị dự báo của một xét nghiệm âm tính, cho ra 490/(1+490) = 0.998, kết quả tương tự như với định lý Bayes.
- a. Tăng ngưỡng cho một ESR dương tính từ ≥20 mm/giờ lên ≥50mm/giờ sẽ làm giảm độ nhạy. b. Sẽ có nhiều dương tính giả hơn vì độ đặc hiệu sẽ giảm. (Ghi chú: câu trả lời gốc dường như có sự nhầm lẫn, tăng ngưỡng sẽ tăng độ đặc hiệu và giảm dương tính giả).
- a. Kết quả dương tính xảy ra 138 lần trong 150 bệnh nhân tiểu đường đã biết = 138/150 = 92% độ nhạy. b. 150 – 24 = 126 kết quả âm tính trong 150 người không bị tiểu đường cho ra 126/150 = 84% độ đặc hiệu. c. Tỷ lệ dương tính giả là 24/150 hay 100% – độ đặc hiệu = 16%. d. Độ nhạy 80% trong 150 người mắc bệnh tiểu đường cho ra 120 dương tính thật. 4% dương tính giả trong 150 người không bị tiểu đường là 6 người. Do đó, khả năng mắc bệnh tiểu đường với một xét nghiệm đường huyết lúc đói dương tính là 120/126 = 95.2%. e. 80% độ nhạy trong 90 (trong số 100) bệnh nhân mắc bệnh tiểu đường = 72 dương tính thật; 4% tỷ lệ dương tính giả trong 10 bệnh nhân không bị tiểu đường = 0.4 dương tính giả. Do đó, 72/72.4 = 0.9945 hay 99.45%, bệnh nhân như người đàn ông này có xét nghiệm đường huyết lúc đói dương tính thực sự mắc bệnh tiểu đường.
- a. Có 80 x 0.19 = 15.2 dương tính thật, và 80 – 15.2 = 64.8 âm tính giả; 20 x 0.82 = 16.4 âm tính thật và 20 – 16.4 = 3.6 dương tính giả. Do đó, xác suất bị nhồi máu cơ tim với một ECG dương tính là 15.2/(15.2+3.6) = 80.9%. b. Xác suất bị nhồi máu cơ tim ngay cả khi xét nghiệm âm tính là 64.8/(64.8+16.4) = 79.8%. c. Những tính toán này minh họa sự vô ích của tiêu chí này (đoạn ST chênh lên ≥5 mm ở các chuyển đạo không tương hợp) trong việc chẩn đoán nhồi máu cơ tim. d. Tỷ số khả dĩ là TP/FP hay 19/18 = 1.06. e. Tỷ lệ chênh trước xét nghiệm là 80/20, hay 4 προς 1. Tỷ lệ chênh sau xét nghiệm là 4 x 1.06 = 4.24. Như bạn có thể thấy, xét nghiệm này rất ít làm thay đổi chỉ số nghi ngờ.
- Xem Hình B-10 để biết các giá trị hữu dụng kỳ vọng cho cây quyết định.
- a. 0.20, thấy ở nhánh trên cùng. b. Không, điều này không rõ ràng. Mặc dù tác giả cung cấp tỷ lệ bệnh nhân có kết quả khám dương tính, 0.26 (và âm tính, 0.74), những con số này bao gồm cả dương tính giả (và âm tính giả) cũng như dương tính thật (và âm tính thật). Tác giả cũng đưa ra giá trị dự báo của một xét nghiệm dương tính, 0.78 (và của một xét nghiệm âm tính, 0.997); và bằng cách sử dụng khá nhiều đại số, chúng ta có thể làm ngược lại để có được các ước tính 0.989 cho độ nhạy và 0.928 cho độ đặc hiệu. Tuy nhiên, không nên mong đợi độc giả của bài báo phải thực hiện những thao tác này; các tác giả nên cung cấp các giá trị chính xác được sử dụng trong bất kỳ phân tích nào. c. Đối với không xét nghiệm hoặc điều trị: (0.20)(48) + (0.80)(100) = 89.6; đối với phẫu thuật cắt bỏ đại tràng: (0.03)(0) + (0.97)[(0.20)(78) + (0.80)(100)] = 92.7. Do đó, nội soi đại tràng là nhánh có giá trị hữu dụng cao nhất, ở mức 94.6.
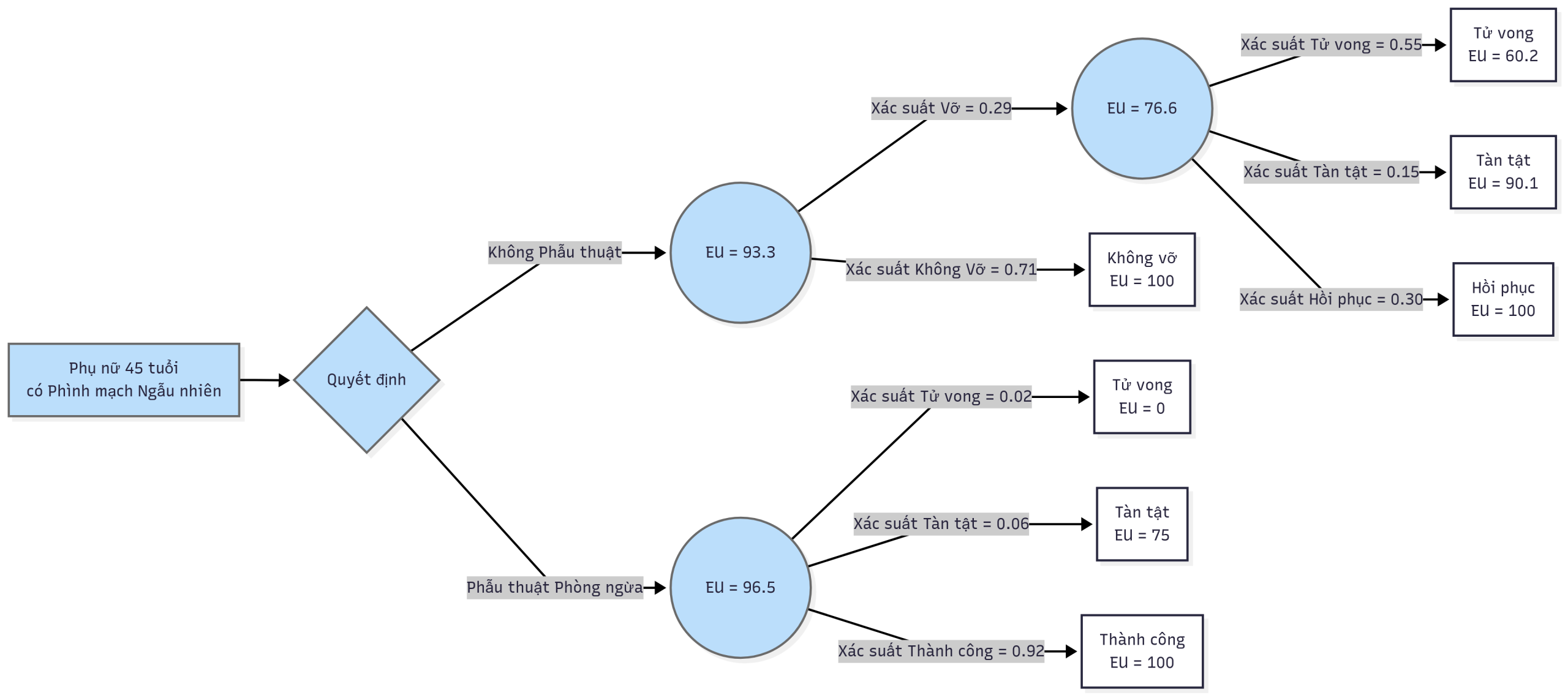
Hình B-10. Cây quyết định cho phình mạch với xác suất và giá trị hữu dụng được bao gồm. (EU = giá trị hữu dụng kỳ vọng.) (Tái bản với sự cho phép từ van Crevel H, Habbema JD, Braakman R: Phân tích quyết định về quản lý phình động mạch nội sọ ngẫu nhiên, Neurology. 1986 Oct;36(10):1335-1339.)
Bảng chú giải thuật ngữ Anh – Việt. Phụ Lục B.
| STT | Tên thuật ngữ tiếng Anh | Phiên âm | Nghĩa tiếng Việt |
|---|---|---|---|
| 1 | Independent | /ˌɪn.dɪˈpen.dənt/ | Độc lập |
| 2 | Probability | /ˌprɒb.əˈbɪl.ə.ti/ | Xác suất |
| 3 | Conditional Probability | /kənˈdɪʃ.ən.əl ˌprɒb.əˈbɪl.ə.ti/ | Xác suất có điều kiện |
| 4 | Chronic | /ˈkrɒn.ɪk/ | Mạn tính |
| 5 | Acute | /əˈkjuːt/ | Cấp tính |
| 6 | Seroconvert | /ˌsɪə.roʊ.kənˈvɜːt/ | Chuyển đổi huyết thanh (Sự thay đổi từ âm tính sang dương tính) |
| 7 | Seropositive | /ˌsɪə.roʊˈpɒz.ə.tɪv/ | Dương tính huyết thanh |
| 8 | Seronegative | /ˌsɪə.roʊˈneɡ.ə.tɪv/ | Âm tính huyết thanh |
| 9 | Binomial Distribution | /baɪˈnoʊ.mi.əl ˌdɪs.trɪˈbjuː.ʃən/ | Phân phối nhị thức |
| 10 | Influenza Virus | /ˌɪn.fluˈen.zə ˈvaɪə.rəs/ | Virus cúm |
| 11 | Infection | /ɪnˈfek.ʃən/ | Sự nhiễm trùng |
| 12 | Survival | /səˈvaɪ.vəl/ | Sự sống sót, sống còn |
| 13 | Patients | /ˈpeɪ.ʃənts/ | Bệnh nhân |
| 14 | Hospitalization | /ˌhɒs.pɪ.təl.aɪˈzeɪ.ʃən/ | Sự nhập viện |
| 15 | Lambda (Poisson distribution parameter) | /ˈlæm.də/ | Lambda (Tham số trong phân phối Poisson) |
| 16 | Poisson Distribution | /ˈpwɑː.sɒn ˌdɪs.trɪˈbjuː.ʃən/ | Phân phối Poisson |
| 17 | Serum Sodium | /ˈsɪə.rəm ˈsoʊ.di.əm/ | Natri huyết thanh |
| 18 | Normal Adult | /ˈnɔː.məl əˈdʌlt/ | Người lớn bình thường |
| 19 | Standard Normal Distribution | /ˈstæn.dəd ˈnɔː.məl ˌdɪs.trɪˈbjuː.ʃən/ | Phân phối chuẩn hóa |
| 20 | Z-distribution | /ziː ˌdɪs.trɪˈbjuː.ʃən/ | Phân phối Z |
| 21 | Mean | /miːn/ | Trung bình |
| 22 | Standard Deviation | /ˈstæn.dəd ˌdiː.viˈeɪ.ʃən/ | Độ lệch chuẩn |
| 23 | Distribution | /ˌdɪs.trɪˈbjuː.ʃən/ | Phân phối |
| 24 | Symmetric | /sɪˈmet.rɪk/ | Đối xứng |
| 25 | Skewed | /skjuːd/ | Lệch, không đối xứng |
| 26 | Observations | /ˌɒb.zəˈveɪ.ʃənz/ | Các quan sát |
| 27 | Population | /ˌpɒp.jəˈleɪ.ʃən/ | Quần thể |
| 28 | Standard Error of the Mean (SE) | /ˈstæn.dəd ˈer.ər əv ðə miːn/ | Sai số chuẩn của trung bình |
| 29 | Individuals | /ˌɪn.dɪˈvɪdʒ.u.əlz/ | Các cá nhân |
| 30 | Area under the curve | /ˈeə.ri.ə ˈʌn.dər ðə kɜːv/ | Diện tích dưới đường cong |
| 31 | Sample size (n) | /ˈsɑːm.pəl saɪz/ | Cỡ mẫu |
| 32 | Critical ratio | /ˈkrɪt.ɪ.kəl ˈreɪ.ʃi.əʊ/ | Tỷ số tới hạn |
| 33 | Limits | /ˈlɪm.ɪts/ | Giới hạn |
| 34 | Intoxicated | /ɪnˈtɒk.sɪ.keɪ.tɪd/ | Say, nhiễm độc |
| 35 | Probability | /ˌprɒb.əˈbɪl.ə.ti/ | Xác suất |
| 36 | Medical students | /ˈmed.ɪ.kəl ˈstjuː.dənts/ | Sinh viên y khoa |
| 37 | Debt | /det/ | Khoản nợ |
| 38 | Retrospective cohort study | /ˌret.rəˈspek.tɪv ˈkoʊ.hɔːt ˈstʌd.i/ | Nghiên cứu thuần tập hồi cứu |
| 39 | Case-control study | /keɪs kənˈtroʊl ˈstʌd.i/ | Nghiên cứu bệnh chứng |
| 40 | Data source | /ˈdeɪ.tə sɔːs/ | Nguồn dữ liệu |
| 41 | Case group | /keɪs ɡruːp/ | Nhóm bệnh |
| 42 | Control group | /kənˈtroʊl ɡruːp/ | Nhóm chứng |
| 43 | Observational study | /ˌɒb.zəˈveɪ.ʃən.əl ˈstʌd.i/ | Nghiên cứu quan sát |
| 44 | Longitudinal study | /ˌlɒn.dʒɪˈtjuː.dɪn.əl ˈstʌd.i/ | Nghiên cứu dọc |
| 45 | Cohort | /ˈkoʊ.hɔːt/ | Quần tập, đoàn hệ |
| 46 | Cancer patients | /ˈkæn.sər ˈpeɪ.ʃənts/ | Bệnh nhân ung thư |
| 47 | Therapy | /ˈθer.ə.pi/ | Liệu pháp, phương pháp điều trị |
| 48 | Self-reported | /self rɪˈpɔː.tɪd/ | Tự báo cáo |
| 49 | Cross-sectional study | /krɒs ˈsek.ʃən.əl ˈstʌd.i/ | Nghiên cứu cắt ngang |
| 50 | Matched case-control study | /mætʃt keɪs kənˈtroʊl ˈstʌd.i/ | Nghiên cứu bệnh chứng bắt cặp |
| 51 | Placebo-controlled | /pləˈsiː.boʊ kənˈtroʊld/ | Có đối chứng với giả dược |
| 52 | Randomized clinical trial | /ˈræn.də.maɪzd ˈklɪn.ɪ.kəl ˈtraɪəl/ | Thử nghiệm lâm sàng ngẫu nhiên |
| 53 | Prospective study | /prəˈspek.tɪv ˈstʌd.i/ | Nghiên cứu tiền cứu |
| 54 | Risk factors | /rɪsk ˈfæk.təz/ | Yếu tố nguy cơ |
| 55 | Cardiovascular morbidity | /ˌkɑː.di.əʊˈvæs.kjə.lər mɔːˈbɪd.ə.ti/ | Bệnh suất tim mạch |
| 56 | Deviations | /ˌdiː.viˈeɪ.ʃənz/ | Độ lệch |
| 57 | Numerical Summary | /njuːˈmer.ɪ.kəl ˈsʌm.ər.i/ | Tóm tắt số liệu |
| 58 | Frequency distribution | /ˈfriː.kwən.si ˌdɪs.trɪˈbjuː.ʃən/ | Phân phối tần suất |
| 59 | Weighted means formula | /ˈweɪ.tɪd miːnz ˈfɔː.mjə.lə/ | Công thức trung bình có trọng số |
| 60 | Midpoint | /ˈmɪd.pɔɪnt/ | Trung điểm |
| 61 | Raw data | /rɔː ˈdeɪ.tə/ | Dữ liệu thô |
| 62 | Class limits | /klɑːs ˈlɪm.ɪts/ | Giới hạn lớp |
| 63 | Odds ratio | /ɒdz ˈreɪ.ʃi.əʊ/ | Tỷ số chênh |
| 64 | Confirmed diagnosis | /kənˈfɜːmd ˌdaɪ.əɡˈnoʊ.sɪs/ | Chẩn đoán đã xác nhận |
| 65 | Inpatient setting | /ˈɪnˌpeɪ.ʃənt ˈset.ɪŋ/ | Môi trường nội trú |
| 66 | Bimodal distribution | /ˌbaɪˈmoʊ.dəl ˌdɪs.trɪˈbjuː.ʃən/ | Phân phối hai đỉnh |
| 67 | Positively skewed | /ˈpɒz.ə.tɪv.li skjuːd/ | Lệch dương |
| 68 | Bell-shaped curve | /bel ʃeɪpt kɜːv/ | Đường cong hình chuông |
| 69 | Median | /ˈmiː.di.ən/ | Trung vị |
| 70 | Range | /reɪndʒ/ | Khoảng biến thiên |
| 71 | Interquartile range | /ˌɪn.tə.kwɔːˈtaɪl reɪndʒ/ | Khoảng tứ phân vị |
| 72 | Standardized ability tests | /ˈstæn.də.daɪzd əˈbɪl.ə.ti tests/ | Các bài kiểm tra năng lực chuẩn hóa |
| 73 | Nominal characteristic | /ˈnɒm.ɪ.nəl ˌkær.ək.təˈrɪs.tɪk/ | Đặc tính danh nghĩa |
| 74 | Proportions | /prəˈpɔː.ʃənz/ | Tỷ lệ |
| 75 | Ordinal scale | /ˈɔː.dɪn.əl skeɪl/ | Thang đo thứ tự |
| 76 | Negatively skewed | /ˈneɡ.ə.tɪv.li skjuːd/ | Lệch âm |
| 77 | Compliance | /kəmˈplaɪ.əns/ | Sự tuân thủ (điều trị) |
| 78 | Correlation | /ˌkɒr.əˈleɪ.ʃən/ | Tương quan |
| 79 | Coefficient of variation | /ˌkoʊ.ɪˈfɪʃ.ənt əv ˌveə.riˈeɪ.ʃən/ | Hệ số biến thiên |
| 80 | Stroke | /stroʊk/ | Đột quỵ |
| 81 | Drug abuse | /drʌɡ əˈbjuːs/ | Lạm dụng thuốc/ma túy |
| 82 | Acetylsalicylic acid (ASA) | /əˌsiː.taɪlˌsæl.ɪˈsɪl.ɪk ˈæs.ɪd/ | Axit acetylsalicylic (Aspirin) |
| 83 | Gastroduodenal mucosa | /ˌɡæs.troʊˌdʒuː.əˈdiː.nəl mjuːˈkoʊ.sə/ | Niêm mạc dạ dày-tá tràng |
| 84 | Experiment | /ɪkˈsper.ɪ.mənt/ | Thí nghiệm, thực nghiệm |
| 85 | Self-controlled trial | /self kənˈtroʊld traɪəl/ | Thử nghiệm tự đối chứng |
| 86 | Dose-response relationship | /doʊs rɪˈspɒns rɪˈleɪ.ʃən.ʃɪp/ | Mối quan hệ liều-đáp ứng |
| 87 | Endoscopic study | /ˌen.dəˈskɒp.ɪk ˈstʌd.i/ | Nghiên cứu nội soi |
| 88 | Placebo | /pləˈsiː.boʊ/ | Giả dược |
| 89 | Extreme values | /ɪkˈstriːm ˈvæl.juːz/ | Giá trị ngoại lai, cực trị |
| 90 | Variability | /ˌveə.ri.əˈbɪl.ə.ti/ | Tính biến thiên, sự thay đổi |
| 91 | pH values | /piːˈeɪtʃ ˈvæl.juːz/ | Các giá trị pH |
| 92 | Figure legend | /ˈfɪɡ.ər ˈledʒ.ənd/ | Chú thích hình |
| 93 | Confidence interval | /ˈkɒn.fɪ.dəns ˈɪn.tə.vəl/ | Khoảng tin cậy |
| 94 | Null hypothesis | /nʌl haɪˈpɒθ.ə.sɪs/ | Giả thuyết không |
| 95 | P-value | /piː ˈvæl.juː/ | Giá trị p |
| 96 | Hypothesis test | /haɪˈpɒθ.ə.sɪs test/ | Kiểm định giả thuyết |
| 97 | Power analysis | /ˈpaʊər əˈnæl.ə.sɪs/ | Phân tích công suất |
| 98 | Wilcoxon test | /wɪlˈkɒk.sən test/ | Kiểm định Wilcoxon |
| 99 | Paired t-test | /peəd tiː test/ | Kiểm định t cặp |
| 100 | Nonparametric procedure | /ˌnɒnˌpær.əˈmet.rɪk prəˈsiː.dʒər/ | Thủ tục phi tham số |
| 101 | One-sample sign-test | /wʌn ˈsɑːm.pəl saɪn test/ | Kiểm định dấu một mẫu |
| 102 | Alternative hypothesis | /ɔːlˈtɜː.nə.tɪv haɪˈpɒθ.ə.sɪs/ | Giả thuyết thay thế |
| 103 | One-sample t-test | /wʌn ˈsɑːm.pəl tiː test/ | Kiểm định t một mẫu |
| 104 | Pooled standard deviation | /puːld ˈstæn.dəd ˌdiː.viˈeɪ.ʃən/ | Độ lệch chuẩn gộp |
| 105 | Degrees of freedom (df) | /dɪˈɡriːz əv ˈfriː.dəm/ | Bậc tự do |
| 106 | Critical value | /ˈkrɪt.ɪ.kəl ˈvæl.juː/ | Giá trị tới hạn |
| 107 | t-statistic | /tiː stəˈtɪs.tɪk/ | Thống kê t |
| 108 | Chi-square test | /ˌkaɪˈskweəd test/ | Kiểm định Khi-bình phương |
| 109 | Expected value | /ɪkˈspek.tɪd ˈvæl.juː/ | Giá trị kỳ vọng |
| 110 | Grand total | /ɡrænd ˈtoʊ.təl/ | Tổng chung |
| 111 | Alpha level (α) | /ˈæl.fə ˈlev.əl/ | Mức alpha (Mức ý nghĩa) |
| 112 | Beta level (β) | /ˈbiː.tə ˈlev.əl/ | Mức beta (Xác suất sai lầm loại II) |
| 113 | ANOVA (Analysis of Variance) | /əˈnoʊ.və/ | Phân tích phương sai |
| 114 | F-ratio | /ef ˈreɪ.ʃi.əʊ/ | Tỷ số F |
| 115 | Tukey’s procedure | /ˈtuː.kiz prəˈsiː.dʒər/ | Thủ tục Tukey |
| 116 | Scheffé’s procedure | /ʃəˈfeɪz prəˈsiː.dʒər/ | Thủ tục Scheffé |
| 117 | Post hoc comparison | /pəʊst hɒk kəmˈpær.ɪ.sən/ | So sánh hậu kiểm |
| 118 | Interaction | /ˌɪn.təˈræk.ʃən/ | Tương tác |
| 119 | Familial vs Sporadic | /fəˈmɪl.i.əl ˈvɜː.səs spəˈræd.ɪk/ | Có tính gia đình và Lẻ tẻ (ngẫu nhiên) |
| 120 | Age at onset | /eɪdʒ ət ˈɒn.set/ | Tuổi khởi phát |
| 121 | Risk Ratio (RR) | /rɪsk ˈreɪ.ʃi.əʊ/ | Tỷ số nguy cơ (Nguy cơ tương đối) |
| 122 | Benzodiazepine | /ˌben.zoʊ.daɪˈæz.ə.piːn/ | Benzodiazepine (Nhóm thuốc an thần) |
| 123 | Alzheimer’s disease | /ˈælt.shaɪ.məz dɪˌziːz/ | Bệnh Alzheimer |
| 124 | Regression coefficient | /rɪˈɡreʃ.ən ˌkoʊ.ɪˈfɪʃ.ənt/ | Hệ số hồi quy |
| 125 | Deep vein thrombosis | /diːp veɪn θrɒmˈboʊ.sɪs/ | Huyết khối tĩnh mạch sâu |
| 126 | Pulmonary embolism | /ˈpʊl.mə.nər.i ˈem.bə.lɪ.zəm/ | Thuyên tắc phổi |
| 127 | Oral contraceptives | /ˈɔː.rəl ˌkɒn.trəˈsep.tɪvz/ | Thuốc tránh thai đường uống |
| 128 | Pearson’s product-moment correlation | /ˈpɪə.sənz ˈprɒd.ʌkt ˈmoʊ.mənt ˌkɒr.əˈleɪ.ʃən/ | Tương quan moment sản phẩm Pearson |
| 129 | Regression line | /rɪˈɡreʃ.ən laɪn/ | Đường hồi quy |
| 130 | Pathogenesis | /ˌpæθ.əˈdʒen.ə.sɪs/ | Sinh bệnh học |
| 131 | Steroid-responsive nephrotic syndrome (SRNS) | /ˈster.ɔɪd rɪˈspɒn.sɪv nɪˈfrɒt.ɪk ˈsɪn.droʊm/ | Hội chứng thận hư đáp ứng steroid |
| 132 | Immune-complex-mediated | /ɪˈmjuːn ˈkɒm.pleks ˈmiː.di.eɪ.tɪd/ | Qua trung gian phức hợp miễn dịch |
| 133 | Circulating immune complexes | /ˈsɜː.kjə.leɪ.tɪŋ ɪˈmjuːn ˈkɒm.plek.sɪz/ | Phức hợp miễn dịch lưu hành |
| 134 | Systemic lupus erythematosus (SLE) | /sɪˈstem.ɪk ˈluː.pəs ˌer.ɪθ.iː.məˈtoʊ.səs/ | Lupus ban đỏ hệ thống |
| 135 | IgG-containing complexes | /ˌaɪ.dʒiːˈdʒiː kənˈteɪ.nɪŋ ˈkɒm.plek.sɪz/ | Các phức hợp chứa IgG |
| 136 | C1q binding | /siː wʌn kjuː ˈbaɪn.dɪŋ/ | Gắn kết C1q |
| 137 | Cause-and-effect relationship | /kɔːz ənd ɪˈfekt rɪˈleɪ.ʃən.ʃɪp/ | Mối quan hệ nhân quả |
| 138 | Kaplan-Meier curve | /ˌkæp.lən ˈmaɪər kɜːv/ | Đường cong Kaplan-Meier |
| 139 | Survival probability | /səˈvaɪ.vəl ˌprɒb.əˈbɪl.ə.ti/ | Xác suất sống sót |
| 140 | Log-rank statistic | /lɒɡ ræŋk stəˈtɪs.tɪk/ | Thống kê log-rank |
| 141 | Covariates | /ˌkoʊˈveə.ri.əts/ | Đồng biến |
| 142 | Median survival | /ˈmiː.di.ən səˈvaɪ.vəl/ | Thời gian sống trung vị |
| 143 | Mantel-Haenszel procedure | /ˈmæn.təl ˈhen.zəl prəˈsiː.dʒər/ | Thủ tục Mantel-Haenszel |
| 144 | Mortality rate | /mɔːˈtæl.ə.ti reɪt/ | Tỷ lệ tử vong |
| 145 | Single-vessel disease | /ˈsɪŋ.ɡəl ˈves.əl dɪˌziːz/ | Bệnh một thân mạch vành |
| 146 | Triple-vessel disease | /ˈtrɪp.əl ˈves.əl dɪˌziːz/ | Bệnh ba thân mạch vành |
| 147 | Left main vessel disease | /left meɪn ˈves.əl dɪˌziːz/ | Bệnh thân chung động mạch vành trái |
| 148 | Adjusted mean | /əˈdʒʌs.tɪd miːn/ | Trung bình đã điều chỉnh |
| 149 | Confounding factor | /kənˈfaʊn.dɪŋ ˈfæk.tər/ | Yếu tố gây nhiễu |
| 150 | Multiple regression | /ˈmʌl.tɪ.pəl rɪˈɡreʃ.ən/ | Hồi quy bội |
