Thống kê Sinh học Cơ bản và Lâm sàng, Ấn bản thứ 5 – Basic & Clinical Biostatistics, 5e
Tác giả: Susan White – Nhà xuất bản McGraw-Hill Medical – Biên dịch: Ths.Bs. Lê Đình Sáng
Chương 7: Câu hỏi Nghiên cứu về Trung bình ở Ba nhóm trở lên
Research Questions About Means in Three or More Groups
CÁC KHÁI NIỆM CHÍNH
|
CÁC VẤN ĐỀ TÌNH HUỐNG
Vấn đề tình huống 1
Bệnh nhân nhiễm HIV có nguy cơ mắc bệnh tim mạch tăng. Dysangco và các đồng nghiệp (2017) đã so sánh một số dấu ấn sinh học (biomarker) cho ba nhóm: 28 bệnh nhân nhiễm HIV đang điều trị bằng thuốc kháng retrovirus (ART), 44 bệnh nhân nhiễm HIV không điều trị bằng ART, và 39 người khỏe mạnh trong nhóm chứng.
Vấn đề tình huống 2
Cornelis và cs (2017) đã tạo ra một thang đo mới để đo lường khả năng thực hiện các hoạt động sinh hoạt hàng ngày (ADL) của các đối tượng bị suy giảm nhận thức. Họ đã tạo ra một thang đo gọi là i-ADL-CDI và thử nghiệm nó trên ba nhóm đối tượng: 79 người khỏe mạnh (nhóm chứng), 73 đối tượng bị suy giảm nhận thức nhẹ (MCI), và 71 bệnh nhân mắc bệnh Alzheimer.
Vấn đề tình huống 3
Durand và cs (2015) đã nghiên cứu lưu lượng máu ở chi dưới bị liệt và không bị liệt ở các đối tượng bị đột quỵ mạn tính (n=10) và nhóm chứng khỏe mạnh (n=10). Lưu lượng máu được đo bằng siêu âm dưới các mức co cơ tự nguyện tối đa (MVC) sau: 20%, 40%, 60%, và 80%. Họ thấy rằng lưu lượng máu sau 80% MVC là yếu tố dự báo tốt nhất về việc chi nào bị liệt.
MỤC ĐÍCH CỦA CHƯƠNG
Nhiều dự án nghiên cứu trong y học sử dụng nhiều hơn hai nhóm, và các kiểm định chi-bình phương được thảo luận trong Chương 6 có thể được mở rộng cho ba nhóm trở lên khi kết quả là một thước đo định tính (hoặc đếm được). Khi kết quả là số, các giá trị trung bình được sử dụng, và các kiểm định t được thảo luận trong Chương 5 và 6 chỉ áp dụng cho việc so sánh hai nhóm. Các nghiên cứu khác xem xét ảnh hưởng của nhiều hơn một yếu tố. Những tình huống này đòi hỏi một kiểm định tổng thể (global, hay omnibus test) để xem liệu có bất kỳ sự khác biệt nào tồn tại trong dữ liệu trước khi kiểm tra các kết hợp trung bình khác nhau để xác định sự khác biệt của từng nhóm.
Nếu không thực hiện kiểm định tổng thể, nhiều kiểm định giữa các cặp trung bình khác nhau sẽ làm thay đổi mức ý nghĩa hay mức α cho toàn bộ thí nghiệm thay vì cho từng so sánh. Ví dụ, Marwick và các đồng nghiệp (1999) đã nghiên cứu mối quan hệ giữa hình ảnh tưới máu cơ tim và tử vong do tim ở nam và nữ. Các yếu tố bao gồm số lượng mạch vành bị ảnh hưởng (không đến ba) và liệu khiếm khuyết tưới máu là cố định hay có thể đảo ngược. Nếu các nhà điều tra này không sử dụng đúng các phương pháp đa biến để phân tích dữ liệu, các phương pháp mà chúng ta thảo luận trong Chương 10, việc so sánh nam và nữ trên 4 x 2 tổ hợp khác nhau của các yếu tố này sẽ tạo ra tám giá trị p. Nếu mỗi so sánh được thực hiện bằng cách sử dụng α = 0.05, cơ hội để mỗi so sánh bị gọi là có ý nghĩa một cách sai lầm là 5%; tức là, một sai lầm loại I có thể xảy ra tám lần khác nhau. Do đó, tổng thể, cơ hội (8 x 5%) để tuyên bố một trong các so sánh có ý nghĩa một cách không chính xác là 40%.¹
Một phương pháp để phân tích dữ liệu bao gồm nhiều quan sát được gọi là phân tích phương sai, viết tắt là ANOVA hoặc anova. Phương pháp này bảo vệ chống lại việc “lạm phát” sai số bằng cách đầu tiên hỏi liệu có bất kỳ sự khác biệt nào tồn tại giữa các trung bình của các nhóm hay không. Nếu kết quả của ANOVA có ý nghĩa thống kê, câu trả lời là có, và sau đó nhà nghiên cứu sẽ thực hiện các so sánh giữa các cặp hoặc các kết hợp nhóm.
Chủ đề phân tích phương sai rất phức tạp, và nhiều sách giáo khoa được dành riêng cho chủ đề này. Tuy nhiên, việc sử dụng nó trong y văn có phần hạn chế, bởi vì các phương pháp hồi quy (xem Chương 10) có thể được sử dụng để trả lời các câu hỏi nghiên cứu tương tự. Mục tiêu của chúng tôi là cung cấp đủ thảo luận để bạn có thể xác định các tình huống mà ANOVA là phù hợp và diễn giải kết quả. Nếu bạn quan tâm đến việc tìm hiểu thêm về phân tích phương sai, hãy tham khảo Berry và các đồng nghiệp (2001) hoặc cuốn sách kinh điển của Dunn và Clark (1987). Ngoại trừ các thiết kế nghiên cứu đơn giản, lời khuyên của chúng tôi cho các nhà nghiên cứu tiến hành một nghiên cứu liên quan đến nhiều hơn hai nhóm hoặc hai biến số trở lên là tham khảo ý kiến của một nhà thống kê để xác định cách phân tích dữ liệu tốt nhất.
¹ Thực ra, 40% chỉ là xấp xỉ đúng; nó không phản ánh thực tế rằng một số so sánh không độc lập.
TỔNG QUAN TRỰC QUAN VỀ ANOVA
Logic của ANOVA
Trong Vấn đề tình huống 1, nồng độ cholesterol lipoprotein mật độ cao (HDL-C) được đo ở ba nhóm đối tượng: nhóm A (39 người nhóm chứng không nhiễm HIV) và nhóm B và C (bệnh nhân nhiễm HIV có hoặc không có điều trị kháng retrovirus [ART]). Các thống kê tóm tắt cho ba trong số các dấu ấn sinh học (ADMA, asymmetric dimethyl arginine; IL-6, interleukin 6; và HDL-C) được nghiên cứu trong nghiên cứu của Dysangco và cs (2017) được hiển thị trong Bảng 7-1.
ANOVA cung cấp một cách để chia tổng biến thiên trong HDL-C của mỗi đối tượng thành hai phần. Giả sử chúng ta ký hiệu HDL-C của một đối tượng là X và xem xét X khác biệt bao nhiêu so với trung bình HDL-C của tất cả các đối tượng trong nghiên cứu, viết tắt là X̅̅. Sự khác biệt này (ký hiệu là X – X̅̅) có thể được chia thành hai phần: sự khác biệt giữa X và trung bình của nhóm mà đối tượng này thuộc về, X̅ⱼ, và sự khác biệt giữa trung bình nhóm và trung bình chung. Bằng ký hiệu, chúng ta viết:
(X – X̅̅) = (X – X̅ⱼ) + (X̅ⱼ – X̅̅)
Bảng 7-1. Giá trị dấu ấn sinh học của nghiên cứu HIV CVD.
|
Nhóm |
ADMA | IL-6 | HCL-C |
|---|---|---|---|
| A (HIV-) (n=38) | 0.59 ± 0.11 (n=35) | 3.29 ± 9.52 (n=38) | 49.84 ± 18.68 |
| B (HIV+ART-) (n=44) | 0.62 ± 0.17 (n=44) | 2.82 ± 2.55 (n=44) | 37.02 ± 10.27ª |
| C (HIV+ART+) (n=28) | 0.47 ± 0.09ᵇ | 1.64 ± 1.16 (n=28) | 41.07 ± 10.77ª |
ADMA, µmol/L asymmetric dimethyl arginine; IL-6, pg/mL, interleukin 6; HDL-C, mg/dL high density lipoprotein cholesterol ª P<0.05 so với A ᵇ P<0.05 so với A và B
Bảng 7-2. Nồng độ các dấu ấn sinh học.
| Nhóm A (HIV-) | ADMA | IL6 | HDLC | Nhóm B (HIV+ART-) | ADMA | IL6 | HDLC | Nhóm C (HIV+ART+) | ADMA | IL6 | HDLC |
|---|---|---|---|---|---|---|---|---|---|---|---|
| HIV- | 0.629 | 0.832 | 78 | HIV+ART- | 0.897 | 2.069 | 44 | HIV+ART+ | 0.565 | 1.2754 | 30 |
| HIV- | 0.489 | 1.611 | 26 | HIV+ART- | 0.577 | 0.3934 | 30 | HIV+ART+ | 0.643 | 1.127 | 38 |
| HIV- | 0.61 | 2.653 | 73 | HIV+ART- | 0.615 | 2.2164 | 32 | HIV+ART+ | 0.564 | 2.43 | 27 |
| HIV- | 0.664 | 3 | 32 | HIV+ART- | 0.636 | 2.3795 | 38 | HIV+ART+ | 0.623 | 0.583 | 39 |
| HIV- | 0.461 | 1.117 | 57 | HIV+ART- | 0.612 | 1.141 | 23 | HIV+ART+ | 0.59 | 1.658 | 30 |
| HIV- | 0.511 | 2.703 | 48 | HIV+ART- | 0.526 | 0.6803 | 61 | HIV+ART+ | 0.403 | 0.48 | 65 |
| HIV- | 0.59 | 1.116 | 39 | HIV+ART- | 0.587 | 2.2574 | 29 | HIV+ART+ | 0.257 | 1.752 | 28 |
| HIV- | 0.591 | 0.622 | 118 | HIV+ART- | 0.629 | 0.9139 | 43 | HIV+ART+ | 0.438 | 0.852 | 40 |
| HIV- | 0.486 | 57.738 | 42 | HIV+ART- | 0.453 | 1.5525 | 29 | HIV+ART+ | 0.51 | 0.785 | 62 |
| HIV- | 0.691 | 2.13 | 35 | HIV+ART- | 0.742 | 1.8025 | 32 | HIV+ART+ | 0.421 | 0.819 | 39 |
| HIV- | 0.559 | 1.878 | 56 | HIV+ART- | 0.722 | 0.9902 | 35 | HIV+ART+ | 0.503 | 0.885 | 42 |
| HIV- | 0.91 | 2.2 | 44 | HIV+ART- | 0.518 | 2.0082 | 32 | HIV+ART+ | 0.422 | 2.031 | 38 |
| HIV- | 0.52 | 2.31 | 47 | HIV+ART- | 0.518 | 3.8902 | 54 | HIV+ART+ | 0.458 | 5.037 | 50 |
| HIV- | 0.534 | 0.716 | 46 | HIV+ART- | 0.676 | 2.0082 | 55 | HIV+ART+ | 0.422 | 4.489 | 33 |
| HIV- | 0.531 | 1.173 | 35 | HIV+ART- | 0.536 | 5.9828 | 48 | HIV+ART+ | 0.511 | 1.489 | 43 |
| HIV- | 0.506 | 1.285 | 59 | HIV+ART- | 0.548 | 2.2549 | 36 | HIV+ART+ | 0.449 | 45 | |
| HIV- | 0.724 | 1.731 | 69 | HIV+ART- | 0.589 | 1.5533 | 33 | HIV+ART+ | 0.402 | 24 | |
| HIV- | 0.783 | 1.855 | 28 | HIV+ART- | 0.35 | 1.8852 | 38 | HIV+ART+ | 0.514 | 1.643 | 34 |
| HIV- | 0.613 | 2.549 | 33 | HIV+ART- | 0.444 | 0.9459 | 26 | HIV+ART+ | 0.54 | 0.887 | 62 |
| HIV- | 0.457 | 1.512 | 42 | HIV+ART- | 0.611 | 7.4926 | 27 | HIV+ART+ | 0.587 | 3.34 | 43 |
| HIV- | 0.525 | 0.929 | 31 | HIV+ART- | 0.409 | 0.7648 | 37 | HIV+ART+ | 0.496 | 1.961 | 41 |
| HIV- | 0.71 | 1.824 | 51 | HIV+ART- | 0.496 | 0.441 | 49 | HIV+ART+ | 0.384 | 0.988 | 34 |
| HIV- | 0.632 | 1.512 | 24 | HIV+ART- | 0.373 | 2.0885 | 48 | HIV+ART+ | 2.4 | 52 | |
| HIV- | 0.572 | 0.726 | 40 | HIV+ART- | 0.499 | 0.6689 | 43 | HIV+ART+ | 0.398 | 0.854 | 40 |
| HIV- | 0.682 | 69 | HIV+ART- | 0.832 | 1.5049 | 34 | HIV+ART+ | 0.471 | 0.48 | 54 | |
| HIV- | 0.477 | 38 | HIV+ART- | 0.368 | 9.0369 | 59 | HIV+ART+ | 0.409 | 0.854 | 28 | |
| HIV- | 0.558 | 45 | HIV+ART- | 0.634 | 2.038 | 31 | HIV+ART+ | 0.384 | 1.803 | 30 | |
| HIV- | 0.672 | 0.996 | 48 | HIV+ART- | 0.564 | 3.578 | 34 | HIV+ART+ | 0.537 | 0.954 | 45 |
| HIV- | 0.587 | 2.608 | 60 | HIV+ART- | 1.024 | 2.901 | 30 | ||||
| HIV- | 0.525 | 2.31 | 42 | HIV+ART- | 0.785 | 2.552 | 28 | ||||
| HIV- | 0.507 | 1.062 | 63 | HIV+ART- | 0.664 | 1.34 | 28 | ||||
| HIV- | 0.527 | 1.354 | 78 | HIV+ART- | 0.614 | 2.038 | 64 | ||||
| HIV- | 0.781 | 5.16 | 39 | HIV+ART- | 1.204 | 3.999 | 24 | ||||
| HIV- | 0.618 | 1.062 | 42 | HIV+ART- | 0.61 | 11.768 | 36 | ||||
| HIV- | 0.589 | 0.76 | 81 | HIV+ART- | 0.52 | 5.736 | 47 | ||||
| HIV- | 0.504 | 0.587 | 47 | HIV+ART- | 0.456 | 3.146 | 42 | ||||
| HIV- | 0.529 | 1.257 | 44 | HIV+ART- | 0.736 | 1.395 | 27 | ||||
| HIV- | 0.81 | 2.19 | 45 | HIV+ART- | 0.581 | 2.901 | 31 | ||||
| HIV+ART- | 0.501 | 1.985 | 37 | ||||||||
| HIV+ART- | 0.735 | 10.57 | 30 | ||||||||
| HIV+ART- | 0.623 | 3.435 | 33 | ||||||||
| HIV+ART- | 0.956 | 2.038 | 45 | ||||||||
| HIV+ART- | 0.778 | 1.505 | 34 | ||||||||
| HIV+ART- | 0.728 | 2.603 | 27 |
Bảng 7-2 chứa các quan sát ban đầu cho các đối tượng trong nghiên cứu. Đối tượng 1 trong nhóm chứng có HDL-C là 78 mg/dL. Trung bình chung cho tất cả các đối tượng là 42.48, vì vậy đối tượng 1 khác với trung bình chung một khoảng là 78 – 42.48, hay 35.52. Sự khác biệt này có thể được chia thành hai phần: sự khác biệt giữa 78 và trung bình của nhóm chứng, 49.84; và sự khác biệt giữa trung bình của nhóm chứng và trung bình chung. Do đó,
(78 – 49.84) + (49.84 – 42.48) = 28.16 + 7.36 = 35.52
Mặc dù ví dụ của chúng ta không cho thấy chính xác cách ANOVA hoạt động, nó minh họa khái niệm chia sự biến thiên thành các phần khác nhau. Ở đây, chúng ta đang xem xét các khác biệt đơn giản liên quan đến chỉ một quan sát; ANOVA xem xét sự biến thiên trong tất cả các quan sát và chia nó thành (1) sự biến thiên giữa mỗi đối tượng và trung bình nhóm của đối tượng đó và (2) sự biến thiên giữa mỗi trung bình nhóm và trung bình chung. Nếu các trung bình nhóm khá khác nhau, sẽ có sự biến thiên đáng kể giữa chúng và trung bình chung, so với sự biến thiên trong mỗi nhóm. Nếu các trung bình nhóm không khác nhau nhiều, sự biến thiên giữa chúng và trung bình chung sẽ không lớn hơn nhiều so với sự biến thiên giữa các đối tượng trong mỗi nhóm. Kiểm định F cho hai phương sai (Chương 6) có thể được sử dụng để kiểm tra tỷ lệ của phương sai giữa các trung bình so với phương sai giữa các đối tượng trong mỗi nhóm.
Giả thuyết H-Không cho kiểm định F là hai phương sai bằng nhau; nếu chúng bằng nhau, sự biến thiên giữa các trung bình không lớn hơn nhiều so với sự biến thiên giữa các quan sát cá nhân trong bất kỳ nhóm nào. Trong tình huống này, chúng ta không thể kết luận rằng các trung bình khác nhau. Do đó, chúng ta coi ANOVA là một kiểm định về sự bằng nhau của các trung bình, mặc dù các phương sai đang được kiểm tra trong quá trình này. Nếu Giả thuyết H-Không bị bác bỏ, chúng ta kết luận rằng không phải tất cả các trung bình đều bằng nhau; tuy nhiên, chúng ta không biết những trung bình nào không bằng nhau, đó là lý do tại sao các quy trình so sánh post hoc là cần thiết.
Minh họa các phép tính trực quan cho ANOVA
Hãy nhớ lại rằng công thức cho phương sai của các quan sát (hoặc bình phương độ lệch chuẩn; xem Chương 3) liên quan đến tổng các bình phương độ lệch của mỗi X so với trung bình X̅:
Một công thức tương tự có thể được sử dụng để tìm phương sai của các trung bình so với trung bình chung:
trong đó nⱼ là số lượng quan sát trong mỗi nhóm và j là số lượng nhóm. Ước tính này được gọi là trung bình bình phương giữa các nhóm, viết tắt là MSₐ, và nó có j-1 bậc tự do.
Để có được phương sai trong các nhóm, chúng ta sử dụng một phương sai gộp giống như phương sai cho kiểm định t cho hai nhóm độc lập:
Ước tính này được gọi là trung bình bình phương sai số (hoặc trung bình bình phương trong nhóm), viết tắt là MSₑ. Nó có Σ(nⱼ-1) bậc tự do, hoặc, nếu tổng số quan sát được ký hiệu là N, nó có N-j bậc tự do. Tỷ số F được hình thành bằng cách chia ước tính phương sai của các trung bình (trung bình bình phương giữa các nhóm) cho ước tính phương sai trong các nhóm (trung bình bình phương sai số), và nó có j-1 và N-j bậc tự do.
Chúng ta sẽ sử dụng dữ liệu từ nghiên cứu của Dysangco và cs (2017) để minh họa các phép tính. Trong ví dụ này, kết quả quan tâm (HDL-C) là biến phụ thuộc, và biến nhóm (đối tượng chứng và hai nhóm bệnh nhân HIV) là biến độc lập. Dữ liệu trong Bảng 7-1 chỉ ra rằng trung bình HDL-C của nhóm B và C, các bệnh nhân HIV, thấp hơn trung bình của nhóm chứng. Nếu ba nhóm đối tượng này được xem là đến từ một tổng thể lớn hơn, thì câu hỏi là liệu nồng độ HDL-C có khác nhau trong tổng thể hay không. Mặc dù có sự khác biệt trong các trung bình ở Bảng 7-1, một số khác biệt trong các mẫu sẽ xảy ra chỉ do ngẫu nhiên, ngay cả khi không có sự biến thiên trong tổng thể. Vì vậy, câu hỏi được rút gọn thành liệu các khác biệt quan sát được có đủ lớn để thuyết phục chúng ta rằng chúng không xảy ra chỉ do ngẫu nhiên mà phản ánh sự khác biệt thực sự trong tổng thể.
Giả thuyết thống kê đang được kiểm tra, Giả thuyết H-Không (Giả thuyết H₀), là trung bình HDL-C bằng nhau giữa ba nhóm. Giả thuyết đối là có sự khác biệt tồn tại; tức là, không phải tất cả các trung bình đều bằng nhau. Các bước kiểm định Giả thuyết H-Không như sau.
Bước 1: H₀: Trung bình HDL-C bằng nhau trong ba nhóm, hay bằng ký hiệu, μ₁ = μ₂ = μ₃. H₁: Các trung bình không bằng nhau, hay bằng ký hiệu, μ₁ ≠ μ₂ hoặc μ₂ ≠ μ₃ hoặc μ₁ ≠ μ₃.
Bước 2: Thống kê kiểm định trong kiểm định sự bằng nhau của các trung bình trong ANOVA là tỷ số F, F = MSₐ / MSₑ, với j-1 và Σ(nⱼ-1) bậc tự do.
Bước 3: Chúng ta sử dụng α = 0.05 cho kiểm định thống kê này.
Bước 4: Giá trị của phân phối F từ Bảng A-4 với j-1=2 bậc tự do ở tử số và Σ(nⱼ-1)=107 ở mẫu số là giữa 3.15 và 3.07; giá trị chính xác từ hàm Excel (=F.INV.RT(0.05,2,107)) là 3.08. Quyết định là bác bỏ Giả thuyết H-Không về các trung bình bằng nhau nếu giá trị quan sát của F lớn hơn 3.08 và rơi vào vùng bác bỏ (Hình 7-1).
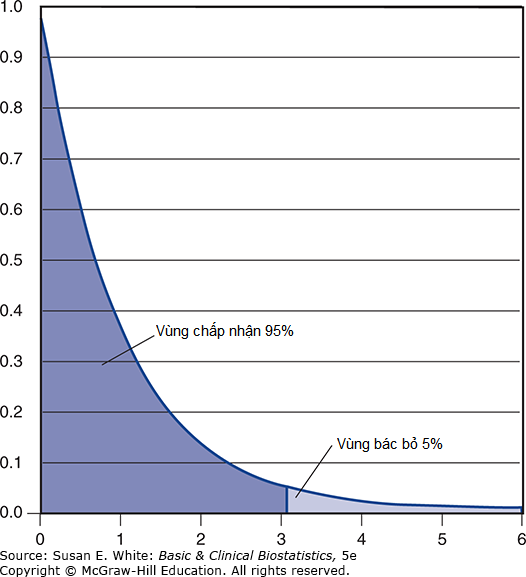
Hình 7-1. Minh họa giá trị tới hạn cho phân phối F với 2 và 107 bậc tự do.
Bước 5: Đầu tiên chúng ta tính trung bình chung. Vì chúng ta đã biết trung bình của ba nhóm, chúng ta có thể tạo một trung bình có trọng số của các trung bình này để tìm trung bình chung:
Tử số của MSₐ là: 38(49.84 – 42.48)² + 44(37.02 – 42.48)² + 28(41.07 – 42.48)² = 3426.6
Đại lượng MSₐ được tìm thấy bằng cách chia tử số cho số nhóm trừ 1, (j-1) – là 2 trong ví dụ này, là:
Các phương sai của từng nhóm được sử dụng để tính ước tính gộp của MSₑ:
Cuối cùng, tỷ số F được tìm thấy bằng cách chia trung bình bình phương giữa các nhóm cho trung bình bình phương sai số:
Bước 6: Giá trị quan sát của tỷ số F là 8.91, lớn hơn 3.08 (giá trị tới hạn từ Bước 4). Do đó, Giả thuyết H-Không về các trung bình bằng nhau bị bác bỏ. Chúng ta kết luận rằng có sự khác biệt tồn tại trong nồng độ HDL-C giữa các đối tượng chứng bình thường, bệnh nhân HIV+ không dùng ART, và bệnh nhân HIV+ đang dùng ART.
Lưu ý rằng việc bác bỏ Giả thuyết H-Không không cho chúng ta biết trung bình của nhóm nào khác biệt, chỉ cho biết rằng có sự khác biệt tồn tại; trong phần có tiêu đề “Các Quy trình So sánh Bội,” chúng ta sẽ minh họa các phương pháp khác nhau có thể được sử dụng để tìm hiểu xem các nhóm cụ thể nào khác biệt.
PHƯƠNG PHÁP ANOVA TRUYỀN THỐNG
Trong phần trước, chúng ta đã trình bày một minh họa đơn giản về ANOVA bằng cách sử dụng các công thức để ước tính phương sai giữa các trung bình của từng nhóm và trung bình chung, được gọi là trung bình bình phương giữa các nhóm (MSₐ), và phương sai trong các nhóm, được gọi là trung bình bình phương sai số hoặc trung bình bình phương trong các nhóm (MSₑ). Theo truyền thống trong ANOVA, các công thức được đưa ra cho tổng các bình phương, thường tương đương với tử số của các công thức được sử dụng trong phần trước; sau đó, tổng các bình phương được chia cho các bậc tự do thích hợp để có được trung bình bình phương. Trước khi minh họa các phép tính cho dữ liệu về nồng độ HDL-C, chúng ta sẽ định nghĩa một số thuật ngữ và đưa ra các công thức truyền thống.
Các thuật ngữ & Công thức cho ANOVA
Trong ANOVA, thuật ngữ yếu tố (factor) đề cập đến biến mà các nhóm được hình thành, tức là biến độc lập. Ví dụ, trong Vấn đề tình huống 1, các đối tượng được chia thành các nhóm dựa trên tình trạng HIV và ART của họ; do đó, nghiên cứu này là một ví dụ về ANOVA một yếu tố, được gọi là ANOVA một chiều. Số lượng nhóm được xác định bởi một yếu tố nhất định được gọi là số mức (levels) của yếu tố; yếu tố trong Vấn đề tình huống 1 có ba nhóm, hoặc chúng ta nói rằng yếu tố nhóm có ba mức. Trong các nghiên cứu thực nghiệm y học, các mức thường được gọi là các phương pháp điều trị (treatments).
Một số sách giáo khoa tiếp cận phân tích phương sai từ góc độ mô hình. Mô hình cho ANOVA một chiều nói rằng một quan sát cá nhân có thể được chia thành ba thành phần liên quan đến (1) trung bình chung, (2) nhóm mà cá nhân đó thuộc về, và (3) chính quan sát cá nhân đó. Để viết mô hình này bằng ký hiệu, chúng ta để i đại diện cho một quan sát cá nhân nhất định và j đại diện cho nhóm mà cá nhân này thuộc về. Khi đó, Xᵢⱼ ký hiệu cho quan sát của cá nhân i trong nhóm j; ví dụ, X₁₁ là quan sát đầu tiên trong nhóm đầu tiên, và X₅₃ là quan sát thứ năm trong nhóm thứ ba. Trung bình chung trong mô hình được ký hiệu là μ. Ảnh hưởng của việc là thành viên của nhóm j có thể được coi là sự khác biệt giữa trung bình của nhóm j và trung bình chung; ảnh hưởng liên quan đến việc ở trong nhóm j được viết là αⱼ. Cuối cùng, sự khác biệt giữa quan sát cá nhân và trung bình của nhóm mà quan sát đó thuộc về được viết là eᵢⱼ và được gọi là sai số (error term), hoặc phần dư (residual). Ghép các ký hiệu này lại, chúng ta có thể viết mô hình cho ANOVA một chiều như sau:
Công thức này nói lên rằng quan sát thứ i trong nhóm thứ j, Xᵢⱼ, là tổng của ba thành phần: trung bình chung, μ; ảnh hưởng liên quan đến nhóm j, αⱼ; và một sai số (phần dư), eᵢⱼ.
Kích thước của một ảnh hưởng, tất nhiên, liên quan đến kích thước của sự khác biệt giữa một trung bình nhóm nhất định và trung bình chung. Khi các suy luận chỉ liên quan đến các mức cụ thể của yếu tố được bao gồm trong nghiên cứu, mô hình được gọi là mô hình hiệu ứng cố định (fixed-effects model). Mô hình hiệu ứng cố định giả định rằng chúng ta chỉ quan tâm đến việc đưa ra các suy luận cho các tổng thể được đại diện trong nghiên cứu. Ví dụ, nếu các nhà điều tra muốn rút ra kết luận về ba mức liều lượng của một loại thuốc. Ngược lại, nếu các mức liều lượng được bao gồm trong nghiên cứu được xem là được chọn ngẫu nhiên từ tất cả các mức liều lượng có thể có của loại thuốc đó, mô hình được gọi là mô hình hiệu ứng ngẫu nhiên (random-effects model), và các suy luận có thể được đưa ra cho các mức khác của yếu tố không được đại diện trong nghiên cứu. Cả hai mô hình đều được sử dụng để kiểm tra các giả thuyết về sự bằng nhau của các trung bình nhóm. Tuy nhiên, mô hình hiệu ứng ngẫu nhiên cũng có thể được sử dụng để kiểm tra các giả thuyết và hình thành các khoảng tin cậy về phương sai của nhóm, và nó còn được gọi là mô hình các thành phần của phương sai vì lý do này.²
Công thức Định nghĩa:
Trong phần “Logic của ANOVA,” chúng ta đã chỉ ra rằng sự biến thiên 35.22 của HDL-C so với trung bình chung 42.48 (đối tượng 1 trong nhóm chứng) có thể được biểu thị dưới dạng tổng của hai khác biệt: (1) sự khác biệt giữa quan sát và trung bình của nhóm nó thuộc về, cộng với (2) sự khác biệt giữa trung bình nhóm của nó và trung bình chung. Kết quả này cũng đúng khi các khác biệt được bình phương và các độ lệch bình phương được cộng lại để tạo thành tổng các bình phương.
Để minh họa, cho một yếu tố với j nhóm, chúng ta sử dụng các định nghĩa sau: Xᵢⱼ là quan sát thứ i trong nhóm thứ j. X̅ⱼ là trung bình của tất cả các quan sát trong nhóm thứ j. X̅̅ là trung bình chung của các quan sát.
Khi đó, Σ(Xᵢⱼ – X̅̅)², tổng bình phương toàn bộ, hay SSₜ, có thể được biểu thị bằng tổng của Σ(Xᵢⱼ – X̅ⱼ)², tổng bình phương sai số (SSₑ) và Σnⱼ(X̅ⱼ – X̅̅)², tổng bình phương giữa các nhóm (SSₐ).
² Việc tính toán tổng các bình phương và trung bình bình phương là như nhau trong cả hai mô hình, nhưng loại mô hình quyết định cách hình thành tỷ số F khi có hai hoặc nhiều yếu tố được bao gồm trong một nghiên cứu.
Nghĩa là, Σ(Xᵢⱼ – X̅̅)² = Σ(Xᵢⱼ – X̅ⱼ)² + Σnⱼ(X̅ⱼ – X̅̅)² hoặc SSₜ = SSₑ + SSₐ.
Chúng tôi không cung cấp chứng minh cho sự bằng nhau này ở đây, nhưng độc giả quan tâm có thể tham khảo bất kỳ tài liệu thống kê tiêu chuẩn nào để biết thêm chi tiết (ví dụ: Berry và cs, 2001; Daniel và Cross, 2018; Hays, 1997).
Công thức Tính toán:
Các công thức tính toán thuận tiện hơn các công thức định nghĩa khi tổng các bình phương được tính thủ công hoặc khi sử dụng máy tính, như tình hình trước khi máy tính trở nên phổ biến. Các công thức tính toán cũng được ưa chuộng hơn vì chúng làm giảm sai số làm tròn. Chúng có thể được suy ra từ các công thức định nghĩa, nhưng vì đại số phức tạp, chúng tôi không giải thích ở đây. Nếu bạn quan tâm đến chi tiết, hãy tham khảo các văn bản đã đề cập trước đó.
Các ký hiệu trong ANOVA có phần khác nhau giữa các văn bản; các công thức sau đây tương tự như các công thức được sử dụng trong nhiều sách và là những công thức chúng tôi sẽ sử dụng để minh họa các phép tính cho ANOVA. Gọi N là tổng số quan sát trong tất cả các nhóm, tức là N = Σnⱼ. Khi đó, các công thức tính toán cho tổng các bình phương là:
và SSₑ được tìm thấy bằng cách trừ: SSₑ = SSₜ – SSₐ.
Tổng các bình phương được chia cho các bậc tự do để có được trung bình bình phương:
trong đó j là số nhóm hoặc mức của yếu tố, và:
trong đó j là số nhóm hoặc mức của yếu tố, và N là tổng cỡ mẫu.
ANOVA một chiều
Vấn đề tình huống 1 là một ví dụ về mô hình ANOVA một chiều trong đó có một biến phụ thuộc dạng số: nồng độ HDL-C. Có ba nhóm bệnh nhân đóng vai trò là biến độc lập: nhóm chứng, và bệnh nhân HIV+ đang dùng hoặc không dùng ART. Mức trung bình của HDL-C được kiểm tra cho các đối tượng trong mỗi nhóm (xem Bảng 7-1).
Minh họa các phép tính truyền thống:
Để tính tổng các bình phương bằng cách sử dụng các công thức ANOVA truyền thống, chúng ta phải có được ba đại lượng:
- Chúng ta bình phương mỗi quan sát (Xᵢⱼ) và cộng lại, để có được ΣXᵢⱼ².
- Chúng ta cộng các quan sát, bình phương tổng, và chia cho N, để có được (ΣXᵢⱼ)² / N.
- Chúng ta bình phương mỗi trung bình (X̅ⱼ), nhân với số đối tượng trong nhóm đó (nⱼ), và cộng lại, để có được ΣnⱼX̅ⱼ².
Sử dụng dữ liệu trong Bảng 7-2, ba đại lượng này là:
ΣXᵢⱼ² = 78² + 26² + … + 30² + 45² = 222517 (ΣXᵢⱼ)² / N = (78+26+…+30+45)² / 110 = 198517.54 ΣnⱼX̅ⱼ² = 38 x 49.84² + 44 x 37.02² + 28 x 41.07² = 201943.11
Sau đó, tổng các bình phương là:
SSₜ = ΣXᵢⱼ² – (ΣXᵢⱼ)² / N = 222517.00 – 198517.54 = 23999.46 SSₐ = ΣnⱼX̅ⱼ² – (ΣXᵢⱼ)² / N = 201943.11 – 198517.54 = 3425.58 SSₑ = SSₜ – SSₐ = 23999.46 – 3425.58 = 20573.88
Tiếp theo, trung bình bình phương được tính toán.
MSₐ = SSₐ / (j-1) = 3425.58 / 2 = 1712.79 MSₑ = SSₑ / (N-j) = 20573.88 / 107 = 192.28
Sự khác biệt nhỏ giữa các kết quả này và kết quả cho trung bình bình phương được tính trong phần “Minh họa các phép tính trực quan cho ANOVA” là do sai số làm tròn. Nếu không, kết quả là như nhau bất kể công thức nào được sử dụng. Cuối cùng, tỷ số F được xác định.
F = MSₐ / MSₑ = 1712.79 / 192.28 = 8.91
Tỷ số F được tính toán được so sánh với giá trị từ phân phối F với 2 và 107 bậc tự do ở mức ý nghĩa mong muốn. Như chúng ta đã tìm thấy trong phần “Minh họa các phép tính trực quan cho ANOVA”, với α=0.05, giá trị của F(2,107) là 3.08. Vì 8.91 lớn hơn 3.08, Giả thuyết H-Không bị bác bỏ; và chúng ta kết luận rằng mức trung bình HDL-C không giống nhau đối với bệnh nhân là HIV- (nhóm chứng), và những người là HIV+ và đang hoặc không đang dùng ART. Các công thức cho ANOVA một chiều được tóm tắt trong Bảng 7-3.
Bảng 7-3. Các công thức cho ANOVA một chiều.
| Nguồn biến thiên | Tổng bình phương (Sums of Squares) | Bậc tự do | Trung bình bình phương (Mean Squares) | Tỷ số F |
|---|---|---|---|---|
| Giữa các nhóm | |
j-1 | |
|
| Sai số | SSₑ = SSₜ – SSₐ | N-j | |
|
| Toàn bộ | |
N-1 |
Các giả định trong ANOVA
Phân tích phương sai sử dụng thông tin về trung bình và độ lệch chuẩn trong mỗi nhóm. Giống như kiểm định t, ANOVA là một phương pháp tham số, và một số giả định quan trọng được đưa ra.
- Các giá trị của biến phụ thuộc hoặc biến kết quả được giả định là phân phối chuẩn trong mỗi nhóm hoặc mức của yếu tố. Trong ví dụ của chúng ta, giả định này yêu cầu nồng độ HDL-C phải có phân phối chuẩn trong mỗi trong ba nhóm.
- Phương sai của tổng thể là như nhau trong mỗi nhóm, tức là, σ₁² = σ₂² = σ₃². Trong ví dụ của chúng ta, điều này có nghĩa là phương sai (hoặc bình phương độ lệch chuẩn) của nồng độ HDL-C phải giống nhau trong mỗi trong ba nhóm.
- Các quan sát là một mẫu ngẫu nhiên, và chúng độc lập ở chỗ giá trị của một quan sát không liên quan đến giá trị của một quan sát khác theo bất kỳ cách nào. Trong ví dụ của chúng ta, giá trị nồng độ HDL-C của một đối tượng không được có ảnh hưởng đến giá trị của bất kỳ đối tượng nào khác.
Không phải tất cả các giả định này đều quan trọng như nhau. Kết quả của kiểm định F không bị ảnh hưởng bởi những sai lệch vừa phải so với tính chuẩn, đặc biệt là đối với một số lượng lớn các quan sát trong mỗi nhóm hoặc mẫu. Nói cách khác, kiểm định F là mạnh (robust) đối với vi phạm giả định về tính chuẩn. Tuy nhiên, nếu các quan sát bị lệch cực độ, đặc biệt là đối với các mẫu nhỏ, nên sử dụng quy trình phi tham số Kruskal-Wallis, được thảo luận sau trong chương này.
Kiểm định F nhạy cảm hơn với giả định thứ hai về phương sai bằng nhau, còn được gọi là tính đồng nhất của phương sai. Tuy nhiên, lo ngại về giả định này được loại bỏ nếu cỡ mẫu bằng nhau (hoặc gần bằng nhau) trong mỗi nhóm (Box, 1953, 1954). Vì lý do này, việc thiết kế các nghiên cứu với cỡ mẫu tương tự là một ý tưởng tốt. Nếu không thể, như đôi khi xảy ra trong các nghiên cứu quan sát, hai giải pháp khác là có thể. Giải pháp thứ nhất là biến đổi dữ liệu trong mỗi nhóm để có được phương sai bằng nhau, sử dụng một trong các phép biến đổi được thảo luận trong Chương 5. Giải pháp thứ hai là chọn các mẫu có kích thước bằng nhau một cách ngẫu nhiên từ mỗi nhóm, mặc dù nhiều nhà điều tra không thích giải pháp này vì các quan sát hoàn toàn tốt bị loại bỏ. Các nhà điều tra nên tham khảo ý kiến của một nhà thống kê cho các nghiên cứu có phương sai rất không bằng nhau và cỡ mẫu không bằng nhau.
Giả định cuối cùng đặc biệt quan trọng. Nói chung, các nhà điều tra nên chắc chắn rằng họ có các quan sát độc lập. Sự độc lập là một vấn đề chủ yếu với các nghiên cứu liên quan đến các phép đo lặp lại trên cùng một đối tượng, và chúng phải được xử lý một cách đặc biệt, như chúng ta sẽ thảo luận sau trong chương này.
Như một nhận xét cuối cùng, hãy nhớ lại rằng mô hình hiệu ứng cố định giả định rằng mỗi quan sát thực sự là một tổng, bao gồm trung bình chung, ảnh hưởng của việc là thành viên của nhóm cụ thể, và sai số (phần dư) đại diện cho bất kỳ sự biến thiên nào không giải thích được. Một số nghiên cứu liên quan đến các quan sát là tỷ lệ, tỷ suất, hoặc tỷ số; và đối với những dữ liệu này, giả định về tổng không đúng.
Diễn giải Vấn đề tình huống 1
Bảng phân tích phương sai cho hoạt độ HCL-C sử dụng R được trình bày trong Bảng 7-4. Yếu tố giữa các nhóm được ký hiệu là A (nhóm) trong hàng đầu tiên của bảng. Chúng ta thấy rằng giá trị tổng bình phương cho yếu tố “giữa các nhóm”, 3,426, gần với giá trị chúng ta đã tính toán trong phần “ANOVA một chiều” (3,425.58). Tương tự, trung bình bình phương và tỷ số F cũng gần với các giá trị chúng ta đã tính.
Bảng 7-4. Bảng phân tích phương sai cho HDL-C (mg/dL).
| Nguồn (Term) | df | Tổng bình phương (Sum of Squares) | Trung bình bình phương (Mean Square) | Tỷ số F (F-Ratio) | Mức xác suất (Probability Level) |
|---|---|---|---|---|---|
| A: Group | 2 | 3,426 | 1,712.8 | 8.908 | 0.000264 |
| S: Error | 107 | 20,574 | 192.3 | ||
| Total | 109 |
Do đó, xác suất quan sát được một sự khác biệt lớn như vậy chỉ do ngẫu nhiên (tức là nếu không có sự khác biệt giữa ba nhóm) là nhỏ hơn 3 trên 10,000. Tác giả đã sử dụng quy trình so sánh Bonferroni và báo cáo rằng nhóm B và C (bệnh nhân HIV+ có và không có ART) khác biệt đáng kể so với nhóm chứng. Chúng ta sẽ thảo luận về thống kê Bonferroni trong phần tiếp theo.
Các nhà điều tra đã kiểm soát các biến gây nhiễu có thể có trong các phân tích theo dõi mà chúng ta sẽ xem xét sau. Các biểu đồ giúp người đọc đánh giá được mức độ của kết quả từ một nghiên cứu. Một biểu đồ hộp về nồng độ HDL-C sử dụng R được đưa ra trong Hình 7-2. Phân tích phương sai chỉ ra rằng có ít nhất một sự khác biệt tồn tại giữa các nhóm. Dựa vào biểu đồ hộp, bạn đoán nhóm nào khác biệt? Trong phần tiếp theo, chúng ta sẽ xem xét các kiểm định thống kê giúp trả lời câu hỏi này.
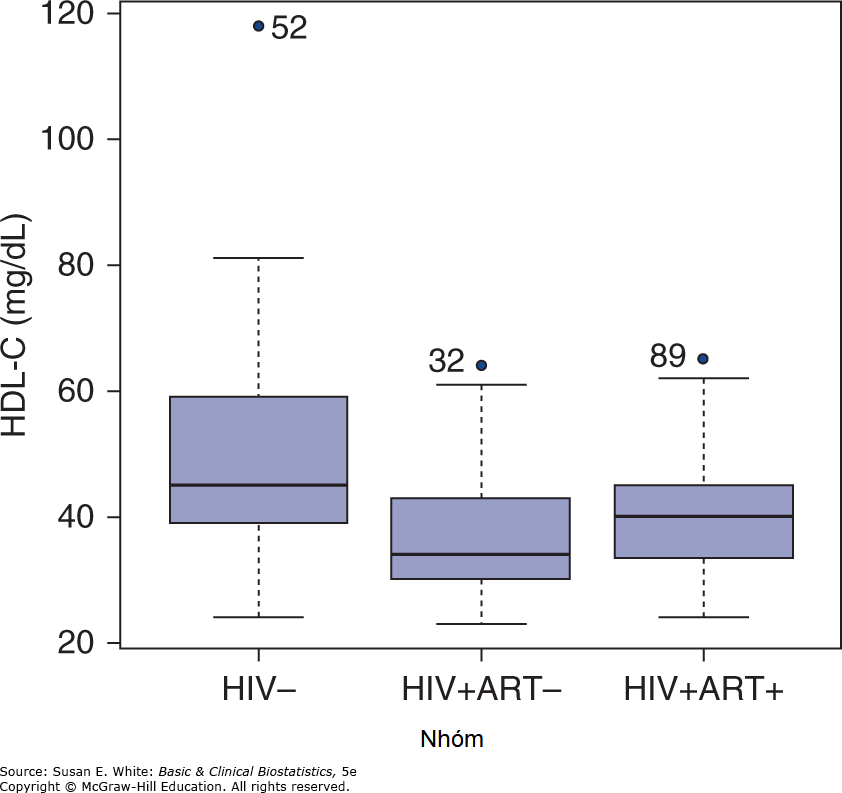
Hình 7-2. Biểu đồ hộp của HDL-C.
CÁC QUY TRÌNH SO SÁNH BỘI
Đôi khi, các nhà nghiên cứu có một số lượng hạn chế các so sánh cụ thể đã được lên kế hoạch, hay còn gọi là so sánh a priori, trong đầu trước khi thiết kế nghiên cứu. Trong tình huống đặc biệt này, các so sánh có thể được thực hiện mà không cần thực hiện ANOVA trước, mặc dù trong thực tế, hầu hết các nhà điều tra vẫn thích thực hiện ANOVA. Thông thường, các nhà nghiên cứu muốn sự tự do và linh hoạt trong việc thực hiện các so sánh được cung cấp bởi các phương pháp posteriori, hay post hoc. Tuy nhiên, trước khi thảo luận về các loại so sánh này, chúng ta cần hai định nghĩa.
Một so sánh hoặc tương phản giữa hai trung bình là sự khác biệt giữa các trung bình, chẳng hạn như μ₁ – μ₂. Các so sánh cũng có thể liên quan đến nhiều hơn hai trung bình. Ví dụ, trong một nghiên cứu để so sánh một loại thuốc mới với giả dược, các nhà điều tra có thể muốn so sánh đáp ứng trung bình cho liều 1 với đáp ứng trung bình cho giả dược, μ₁ – μₚ, cũng như đáp ứng trung bình cho liều 2 với đáp ứng trung bình cho giả dược, μ₂ – μₚ. Ngoài ra, họ có thể muốn so sánh hiệu quả tổng thể của thuốc với hiệu quả của giả dược [(μ₁ + μ₂)/2] – μₚ. Lưu ý rằng trong tất cả các ví dụ, các hệ số của các trung bình cộng lại bằng 0; tức là, viết lại so sánh đầu tiên một chút ta có (1)μ₁ + (-1)μ₂ và (1) + (-1) = 0; viết lại so sánh cuối cùng ta có (1/2)μ₁ + (1/2)μ₂ + (-1)μₚ và (1/2) + (1/2) + (-1) một lần nữa bằng 0.
Định nghĩa thứ hai liên quan đến sự phân biệt giữa hai loại so sánh hoặc tương phản khác nhau. Hai so sánh là trực giao (orthogonal) nếu chúng không sử dụng cùng một thông tin. Ví dụ, giả sử một nghiên cứu liên quan đến bốn liệu pháp khác nhau: 1, 2, 3, và 4. Khi đó, so sánh giữa μ₁ – μ₂ và giữa μ₃ – μ₄ là trực giao vì thông tin được sử dụng để so sánh nhóm 1 và 2 không phải là thông tin được sử dụng để so sánh nhóm 3 và 4. Theo một nghĩa nào đó, các câu hỏi được đặt ra bởi hai so sánh trực giao có thể được coi là độc lập với nhau. Ngược lại, so sánh μ₁ – μ₂ và μ₁ – μ₃ không trực giao vì chúng sử dụng thông tin dư thừa; tức là, các quan sát trong nhóm 1 được sử dụng trong cả hai so sánh.
So sánh A Priori, hay So sánh có kế hoạch
Khi các so sánh được lên kế hoạch, chúng có thể được thực hiện mà không cần thực hiện ANOVA trước. Khi tất cả các so sánh đều trực giao, kiểm định t cho các nhóm độc lập (xem Chương 6) có thể được sử dụng để so sánh hai nhóm với sửa đổi sau: thay vì sử dụng độ lệch chuẩn gộp SDₚ trong mẫu số của tỷ số, chúng ta sử dụng trung bình bình phương sai số MSₑ. Khi cỡ mẫu bằng nhau, ký hiệu là n, tỷ số trở thành:
với N-j bậc tự do, trong đó N là tổng số quan sát, n₁ + n₂, trong hai nhóm.
Điều chỉnh mức α giảm xuống:
Khi thực hiện nhiều so sánh có kế hoạch, xác suất đạt được ý nghĩa do ngẫu nhiên tăng lên; cụ thể là, xác suất của sai lầm loại I tăng lên. Ví dụ, đối với bốn so sánh độc lập, tất cả ở α=0.05, xác suất có một hoặc nhiều kết quả có ý nghĩa là 4 x 0.05 = 0.20. Một cách để bù trừ cho nhiều so sánh (trực giao) là giảm mức α, và điều này có thể được thực hiện bằng cách chia α cho số lượng so sánh được thực hiện. Ví dụ, nếu thực hiện bốn so sánh độc lập, α được chia cho 4 để có được α cho mỗi so sánh là 0.05/4 = 0.0125 để duy trì xác suất tổng thể của sai lầm loại I ở mức 0.05. Sử dụng phương pháp này, mỗi so sánh trực giao phải có ý nghĩa ở mức 0.0125 để có ý nghĩa thống kê.
Quy trình Bonferroni t:
Một cách tiếp cận khác cho các so sánh có kế hoạch là phương pháp Bonferroni t, còn được gọi là quy trình so sánh bội của Dunn. Cách tiếp cận này linh hoạt hơn vì nó có thể áp dụng cho cả so sánh trực giao và không trực giao. Phương pháp Bonferroni t làm tăng giá trị F tới hạn cần thiết để so sánh được tuyên bố là có ý nghĩa. Mức độ tăng phụ thuộc vào số lượng so sánh và cỡ mẫu.
Để minh họa, hãy xem xét ba nhóm trong Vấn đề tình huống 1. Chúng ta sẽ sử dụng các khác biệt cặp cho nồng độ HDL-C được liệt kê trong Bảng 7-5 để minh họa tất cả các so sánh bội trong phần này để chúng ta có thể so sánh kết quả của các quy trình khác nhau. Để đơn giản hóa các minh họa của chúng ta, chúng ta giả định số đối tượng là 40 trong mỗi nhóm (các chương trình máy tính sẽ điều chỉnh cho các cỡ mẫu khác nhau).
Trong quy trình Bonferroni t, √(2MSₑ/n) được nhân với một hệ số liên quan đến số lượng so sánh được thực hiện và bậc tự do của trung bình bình phương sai số. Trong ví dụ này, có ba so sánh cặp; đối với α=0.05 và giả sử có khoảng 120 bậc tự do, hệ số nhân là 2.43 (xem Bảng 7-6).
Do đó,
trong đó giá trị của MSₑ đến từ kết quả của ANOVA (Bảng 7-4). Sự khác biệt trung bình giữa nhóm B và C được so sánh với 7.53. Sự khác biệt trung bình giữa nhóm B và C chỉ là -4.05 và không có ý nghĩa thống kê. Tuy nhiên, cả hai khác biệt trung bình giữa nhóm A và C và nhóm A và B đều có ý nghĩa thống kê: cả 12.82 và 8.77 đều vượt quá 7.53. Chúng ta kết luận rằng bệnh nhân HIV+ cả đang và không đang dùng ART có nồng độ HDL-C khác với các đối tượng chứng. Kết luận này có phù hợp với dự đoán tốt nhất của bạn sau khi xem các biểu đồ hộp trong Hình 7-2 không?
Bảng 7-5. Khác biệt giữa các trung bình của các nhóm HDL-C (mg/dL).
| X̅ₐ | X̅ₑ | X̅_c | |
|---|---|---|---|
| X̅ₐ | 12.82 | 8.77 | |
| X̅ₑ | -4.05 | ||
| X̅_c |
Bảng 7-6. Trích đoạn bảng sử dụng cho các quy trình so sánh bội với α=0.05.
| Bậc tự do sai số | Số trung bình/bước cho Dải Student hóa | Số trung bình cho Kiểm định Dunnett | Số so sánh cho Bonferroni t |
|---|---|---|---|
| 2 / 3 / 4 | 2 / 3 / 4 | 2 / 3 / 4 / 5 / 6 | |
| 120 | 2.80 / 3.36 / 3.68 | 1.66 / 1.93 / 2.08 | 2.27 / 2.43 / 2.54 / 2.62 / 2.68 |
So sánh A Posteriori, hay Post Hoc
So sánh post hoc (thuật ngữ Latin có nghĩa là “sau đó”) được thực hiện sau khi ANOVA cho kết quả là một kiểm định F có ý nghĩa. Kiểm định t được giới thiệu trong Chương 5 không nên được sử dụng cho các so sánh này vì nó không tính đến số lượng so sánh đang được thực hiện, khả năng thiếu độc lập của các so sánh, và bản chất không có kế hoạch của các so sánh.
Có một số quy trình có sẵn để thực hiện so sánh post hoc. Bốn trong số đó được các nhà thống kê khuyên dùng, tùy thuộc vào thiết kế nghiên cứu cụ thể, và hai quy trình khác không được khuyên dùng nhưng vẫn được sử dụng phổ biến. Dữ liệu từ Vấn đề tình huống 1, như được tóm tắt trong Bảng 7-5, một lần nữa được sử dụng để minh họa sáu quy trình này. Tương tự như phương pháp Bonferroni t, cần có các bảng đặc biệt để tìm các hệ số nhân thích hợp cho các kiểm định này khi không sử dụng các chương trình máy tính để phân tích; các trích đoạn từ các bảng được sao chép trong Bảng 7-6 tương ứng với α=0.05.
Quy trình HSD của Tukey:
Quy trình đầu tiên chúng ta thảo luận là kiểm định Tukey, hay kiểm định HSD (honestly significant difference) của Tukey, được đặt tên như vậy vì một số quy trình post hoc làm cho việc đạt được ý nghĩa trở nên quá dễ dàng. Nó được phát triển bởi cùng một nhà thống kê đã phát minh ra biểu đồ thân-lá và biểu đồ hộp-râu, và ông rõ ràng có khiếu hài hước. Kiểm định HSD của Tukey chỉ có thể được sử dụng cho các so sánh cặp, nhưng nó cho phép nhà nghiên cứu so sánh tất cả các cặp trung bình. Một nghiên cứu của Stoline (1981) cho thấy đây là quy trình chính xác và mạnh mẽ nhất để sử dụng trong tình huống này. (Hãy nhớ lại rằng công suất là khả năng phát hiện ra sự khác biệt nếu nó thực sự tồn tại, và Giả thuyết H-Không được bác bỏ một cách chính xác thường xuyên hơn.)
Thống kê HSD, giống như Bonferroni t, có một hệ số nhân dựa trên số lượng mức xử lý và bậc tự do của trung bình bình phương sai số (3 và khoảng 120 trong ví dụ này). Trong Bảng 7-6, dưới cột 3 và cho dải student hóa, chúng ta tìm thấy hệ số nhân là 3.36.
Thống kê HSD là:
trong đó n là cỡ mẫu trong mỗi nhóm.
Do đó,
Các khác biệt trong Bảng 7-5 bây giờ được so sánh với 7.37 và có ý nghĩa thống kê nếu chúng vượt quá giá trị này. Các khác biệt giữa nhóm A và B và nhóm A và C lớn hơn 7.37. Kết luận giống như với Bonferroni rằng bệnh nhân HIV+ cả đang và không đang dùng ART có giá trị HDL-C khác với nhóm chứng; tuy nhiên, không có sự khác biệt nào tồn tại giữa hai nhóm HIV+. Quy trình của Tukey cũng có thể được sử dụng để hình thành các khoảng tin cậy về sự khác biệt trung bình (cũng như phương pháp Bonferroni t). Ví dụ, khoảng tin cậy 95% cho sự khác biệt trung bình giữa bệnh nhân HIV+ không dùng ART và nhóm chứng là: (X̅₁ – X̅₂) ± 7.37 → 12.82 ± 7.37 hay 5.45 đến 20.19
Quy trình Scheffé:
Quy trình Scheffé là quy trình linh hoạt nhất trong tất cả các phương pháp post hoc vì nó cho phép nhà nghiên cứu thực hiện tất cả các loại so sánh, không chỉ đơn giản là so sánh cặp. Ví dụ, quy trình Scheffé cho phép chúng ta so sánh trung bình tổng thể của hai hoặc nhiều mức liều lượng với một giả dược.
Tuy nhiên, một cái giá phải trả cho sự linh hoạt này: một giá trị tới hạn cao hơn được sử dụng để xác định ý nghĩa, làm cho quy trình Scheffé trở thành quy trình bảo thủ nhất trong các quy trình so sánh bội.
Công thức, trông có vẻ phức tạp, là:
trong đó j là số nhóm, Fα,df là giá trị tới hạn của F được sử dụng trong ANOVA, MSₑ là trung bình bình phương sai số, và Σ(Cⱼ²/nⱼ) là tổng các hệ số bình phương chia cho cỡ mẫu trong tương phản quan tâm. Ví dụ, trong tương phản được xác định bằng cách so sánh bệnh nhân đang dùng và không dùng ART (vẫn giả sử có 40 bệnh nhân trong mỗi nhóm), ΣCⱼ²/nⱼ = (1)²/40 + (-1)²/40 = 0.05
Giá trị tới hạn cho F được tìm thấy là 3.08 trong phần “Tổng quan trực quan về ANOVA”.
Thay các giá trị vào S ta được:
Do đó, bất kỳ tương phản nào lớn hơn 7.69 đều có ý nghĩa. Như chúng ta thấy từ Bảng 7-5, sự khác biệt về trung bình giữa bệnh nhân HIV+ (cả đang và không đang dùng ART) và nhóm chứng đều lớn hơn 7.69 và có ý nghĩa theo quy trình Scheffé. Vì quy trình Scheffé là quy trình bảo thủ nhất trong tất cả các kiểm định post hoc, 7.69 là giá trị tới hạn lớn nhất được yêu cầu bởi bất kỳ quy trình so sánh bội nào. Các khoảng tin cậy cũng có thể được hình thành bằng cách sử dụng quy trình Scheffé.
Quy trình Newman-Keuls:
Tiếp theo, chúng ta xem xét quy trình Newman-Keuls. Thường được sử dụng trong nghiên cứu khoa học cơ bản, Newman-Keuls sử dụng một cách tiếp cận từng bước để kiểm tra sự khác biệt giữa các trung bình và chỉ có thể được sử dụng để thực hiện các so sánh cặp. Quy trình xếp hạng các trung bình từ thấp nhất đến cao nhất, và số bước ngăn cách các cặp trung bình được ghi nhận. Đối với ví dụ của chúng ta, thứ tự xếp hạng và số bước được đưa ra trong Hình 7-3. Các khác biệt trung bình được so sánh với một giá trị tới hạn phụ thuộc vào số bước giữa hai trung bình, cỡ mẫu, và số nhóm được so sánh. Ngoài ra, việc kiểm tra phải được thực hiện theo một trình tự quy định.
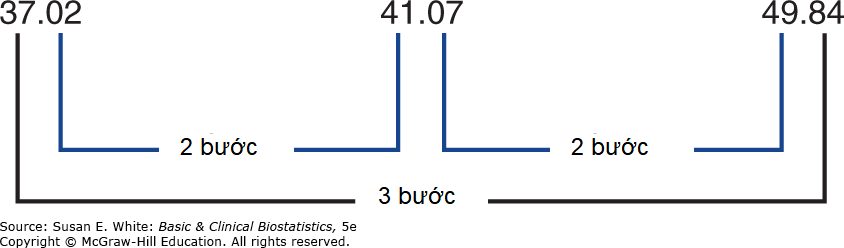
Hình 7-3. Xếp hạng các trung bình và các bước cho quy trình Newman-Keuls.
Giá trị tới hạn sử dụng dải student hóa, nhưng giá trị tương ứng với số bước giữa các trung bình (thay vì số trung bình, như trong kiểm định Tukey); giá trị này được nhân với √(MSₑ/n) như trong kiểm định Tukey. Giá trị từ Bảng 7-6 tương ứng với hai bước với 120 bậc tự do là 2.80; giá trị cho ba bước là 3.36.
Do đó, các giá trị tới hạn cho ví dụ này là:
Tương tự như các quy trình khác, kết luận là các đối tượng chứng và bệnh nhân HIV+ cả đang và không đang dùng ART có nồng độ HDL-C khác với nhóm chứng; tuy nhiên, không có sự khác biệt nào tồn tại giữa bệnh nhân HIV+ đang và không đang dùng ART. Mặc dù kết luận giống như trong kiểm định Tukey trong ví dụ này, việc sử dụng quy trình Newman-Keuls với nhiều nhóm có thể cho phép nhà điều tra tuyên bố một sự khác biệt giữa hai bước là có ý nghĩa khi nó sẽ không có ý nghĩa trong kiểm định HSD của Tukey. Nhược điểm chính của quy trình Newman-Keuls là không thể hình thành các khoảng tin cậy cho sự khác biệt trung bình.
Quy trình Dunnett:
Quy trình thứ tư được các nhà thống kê khuyên dùng được gọi là quy trình Dunnett, và nó chỉ áp dụng trong các tình huống mà một số trung bình điều trị được so sánh với một trung bình chứng duy nhất. Không có so sánh nào được phép giữa các trung bình điều trị với nhau, vì vậy kiểm định này có một ứng dụng rất chuyên biệt. Tuy nhiên, khi có thể áp dụng, quy trình Dunnett rất thuận tiện vì nó có một giá trị tới hạn tương đối thấp. Kích thước của hệ số nhân phụ thuộc vào số lượng nhóm, bao gồm cả nhóm chứng, và bậc tự do của trung bình bình phương sai số.
Công thức là:
Mặc dù quy trình Dunnett không áp dụng cho ví dụ của chúng ta, chúng ta sẽ xác định giá trị tới hạn để so sánh. Từ Bảng 7-6, dưới cột cho quy trình Dunnett và ba nhóm, chúng ta tìm thấy hệ số nhân là 1.93. Nhân nó với √(2MSₑ/n) cho ra 1.93 x 3.10, hay 5.98, một giá trị thấp hơn nhiều so với cả giá trị Tukey hoặc Scheffé.
Các Kiểm định khác:
Hai quy trình xuất hiện trong y văn nhưng không được các nhà thống kê khuyên dùng là kiểm định phạm vi bội mới của Duncan và kiểm định khác biệt có ý nghĩa nhỏ nhất (LSD). Kiểm định phạm vi bội mới của Duncan sử dụng cùng nguyên tắc như quy trình Newman-Keuls; tuy nhiên, các hệ số nhân trong công thức nhỏ hơn, vì vậy các khác biệt có ý nghĩa thống kê được tìm thấy với các khác biệt trung bình nhỏ hơn. Duncan cho rằng khả năng tìm thấy sự khác biệt lớn hơn với số lượng nhóm lớn hơn, và ông đã tăng công suất của kiểm định bằng cách sử dụng các hệ số nhân nhỏ hơn. Nhưng kết quả là, kiểm định của ông quá tự do và bác bỏ Giả thuyết H-Không quá thường xuyên. Do đó, nó không được các nhà thống kê khuyên dùng.
Kiểm định khác biệt có ý nghĩa nhỏ nhất (LSD) là một trong những quy trình so sánh bội lâu đời nhất. Tương tự như các quy trình post hoc khác, nó yêu cầu một tỷ số F có ý nghĩa từ ANOVA để thực hiện các so sánh cặp. Tuy nhiên, thay vì sử dụng một sự điều chỉnh để làm cho giá trị tới hạn lớn hơn, như các kiểm định khác đã làm, kiểm định LSD sử dụng phân phối t tương ứng với số bậc tự do của trung bình bình phương sai số. Các nhà thống kê không khuyên dùng kiểm định này vì, với một số lượng lớn các so sánh, các khác biệt quá nhỏ có thể bị tuyên bố là có ý nghĩa một cách không chính xác.
Như chúng ta vừa minh họa, các quy trình so sánh bội rất tẻ nhạt để tính toán; may mắn thay, chúng có sẵn trong hầu hết các chương trình phần mềm thống kê. Kết quả từ kiểm định so sánh bội của Tukey sử dụng chương trình R được sao chép trong Bảng 7-7. R cũng tạo ra một tập hợp các khoảng tin cậy đồng thời cho các khác biệt cặp như được hiển thị trong Hình 7-4. Điều này cho phép người đọc dễ dàng biết được khác biệt nào là có ý nghĩa bằng cách lưu ý khoảng tin cậy nào không đi qua giá trị 0. Các kết luận từ đồ thị có đồng ý với những phát hiện của chúng ta không?
Bảng 7-7. So sánh bội các trung bình: Tương phản Tukey.
| So sánh tuyến tính | Ước tính (Estimate) | Lỗi chuẩn (Std. Error) | giá trị t (t value) | Pr(>|t|) |
|---|---|---|---|---|
| HIV+ART- – HIV- == 0 | -12.819 | 3.071 | -4.175 | 0.000197 *** |
| HIV+ART+ – HIV- == 0 | -8.771 | 3.454 | -2.540 | 0.033166 * |
| HIV+ART+ – HIV+ART- == 0 | 4.049 | 3.352 | 1.208 | 0.450512 |
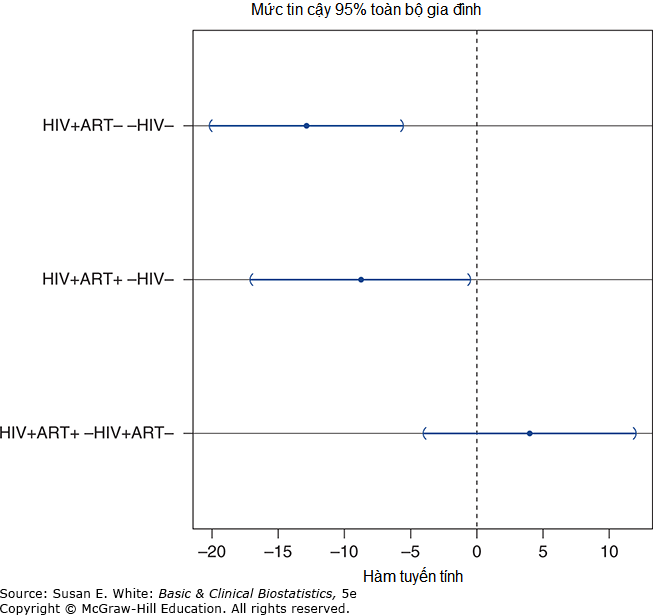
Hình 7-4. Đồ thị khoảng tin cậy đồng thời 95% cho chênh lệch cặp trong HDL-C.
CÁC MINH HỌA BỔ SUNG VỀ VIỆC SỬ DỤNG ANOVA
Trong phần này, chúng ta mở rộng việc sử dụng phân tích phương sai cho một số thiết kế quan trọng khác được sử dụng trong lĩnh vực y tế. Hầu hết các thiết kế ANOVA là sự kết hợp của một số lượng tương đối nhỏ các thiết kế: thiết kế giai thừa ngẫu nhiên, thiết kế khối ngẫu nhiên, và thiết kế hình vuông Latin. Nguyên tắc phân công ngẫu nhiên là kết quả từ công trình của hai nhà thống kê vào đầu thế kỷ XX, Ronald Fisher và Karl Pearson, những người có ảnh hưởng đáng kể đến sự phát triển và định hướng của các phương pháp thống kê hiện đại. Vì lý do này, thuật ngữ “ngẫu nhiên” xuất hiện trong tên của nhiều thiết kế; hãy nhớ lại rằng một trong những giả định là một mẫu ngẫu nhiên đã được phân công cho các mức xử lý khác nhau.
ANOVA Hai chiều: Thiết kế Giai thừa
ANOVA hai chiều tương tự như ANOVA một chiều ngoại trừ việc hai yếu tố (hoặc hai biến độc lập) được phân tích. Ví dụ, trong nghiên cứu được mô tả trong Vấn đề tình huống 2, Cornelis và các đồng nghiệp (2017) muốn biết liệu có sự khác biệt trong một thang đo tổng hợp về các hoạt động sinh hoạt hàng ngày (ADL) đối với các đối tượng có các mức độ suy giảm nhận thức khác nhau hay không. Đối với ví dụ này, chúng tôi sẽ mở rộng nghiên cứu để so sánh ảnh hưởng của giới tính và chỉ bao gồm hai trong số các nhóm suy giảm: suy giảm nhận thức nhẹ (MCI) và các đối tượng mắc bệnh Alzheimer (AD). Họ đã tạo ra một thang đo mới để đo lường sự suy giảm chức năng ADL (i-ADL-CDI). Dữ liệu tóm tắt được đưa ra trong Bảng 7-8. Trong ví dụ này, cả hai yếu tố đều được đo ở hai mức trên tất cả các đối tượng và được cho là chéo nhau (crossed).
Bảng 7-8. Điểm số Hoạt động Sinh hoạt Hàng ngày cho các đối tượng trong các nhóm khác nhau.
| Thống kê nhóm | n | Trung bình i-ADL-CDI | SD i-ADL-CDI |
|---|---|---|---|
| Suy giảm Nhận thức nhẹ | 73 | 0.19 | 0.19 |
| Nữ | 31 | 0.20 | 0.18 |
| Nam | 42 | 0.19 | 0.20 |
| Bệnh Alzheimer | 71 | 0.43 | 0.22 |
| Nữ | 23 | 0.53 | 0.22 |
| Nam | 48 | 0.39 | 0.20 |
Bởi vì hai yếu tố được phân tích trong nghiên cứu này (mức độ suy giảm và giới tính), mỗi yếu tố được đo ở hai mức (AD so với MCI và nam so với nữ), 2 x 2 = 4 tổ hợp xử lý là có thể: đối tượng nữ mắc AD, đối tượng nữ mắc MCI, đối tượng nam mắc AD, và đối tượng nam mắc MCI. Ba câu hỏi có thể được đặt ra trong ANOVA hai chiều này:
- Có sự khác biệt giữa các đối tượng AD và MCI không? Nếu có, các trung bình cho mỗi tổ hợp xử lý có thể giống với các giá trị giả định được đưa ra trong Bảng 7-9A, và chúng ta nói rằng có sự khác biệt trong hiệu ứng chính (main effect) của tình trạng nhận thức. Giả thuyết H-Không cho câu hỏi này là i-ADL-CDI là như nhau ở các đối tượng AD và ở các đối tượng MCI (μₐ = μₘ).
- Có sự khác biệt giữa các đối tượng nam và nữ không? Nếu có, các trung bình cho mỗi tổ hợp xử lý có thể tương tự như các giá trị trong Bảng 7-9B, và chúng ta nói rằng có sự khác biệt trong hiệu ứng chính của giới tính. Giả thuyết H-Không cho câu hỏi này là i-ADL-CDI là như nhau ở các đối tượng nam và ở các đối tượng nữ (μₘ = μբ).
- Có sự khác biệt nào không phải do riêng tình trạng nhận thức hay giới tính mà do sự kết hợp của các yếu tố không? Nếu có, các trung bình cho mỗi tổ hợp xử lý có thể giống với các giá trị trong Bảng 7-9C, và chúng ta nói rằng có hiệu ứng tương tác (interaction effect) giữa hai yếu tố. Giả thuyết H-Không cho câu hỏi này là bất kỳ sự khác biệt nào về ADL giữa các đối tượng nam mắc AD và các đối tượng nam mắc MCI cũng giống như sự khác biệt giữa các đối tượng nữ mắc AD và các đối tượng nữ mắc MCI (μₘₐ – μₘₘ = μբₐ – μբₘ).
Nghiên cứu này có thể được xem như hai thí nghiệm riêng biệt trên cùng một tập hợp đối tượng cho mỗi trong hai câu hỏi đầu tiên. Tuy nhiên, câu hỏi thứ ba chỉ có thể được trả lời trong một thí nghiệm duy nhất trong đó cả hai yếu tố đều được đo lường và có nhiều hơn một quan sát được thực hiện ở mỗi tổ hợp xử lý của các yếu tố (tức là, trong mỗi ô).
Chủ đề về tương tác rất quan trọng và đáng để tìm hiểu sâu hơn một chút. Hình 7-5A là một đồ thị của các mức i-ADL-CDI trung bình giả định từ Bảng 7-9A cho AD và MCI, nam và nữ. Khi các đường nối các trung bình song song, không có tương tác giữa các yếu tố tình trạng nhận thức và tình trạng giới tính, và các hiệu ứng được cho là cộng tính (additive). Tuy nhiên, nếu tương tác có ý nghĩa, như trong Bảng 7-9C, các đường cắt nhau và các hiệu ứng được gọi là nhân tính (multiplicative). Hình 7-5B minh họa tình huống này và cho thấy rằng các hiệu ứng chính, chẳng hạn như tình trạng nhận thức và tình trạng giới tính, khó diễn giải khi có các tương tác có ý nghĩa. Ví dụ, nếu tương tác có ý nghĩa, bất kỳ kết luận nào liên quan đến sự khác biệt về i-ADL-CDI đều phụ thuộc vào cả tình trạng nhận thức và giới tính; bất kỳ so sánh nào giữa các đối tượng mắc AD và MCI đều phụ thuộc vào giới tính của đối tượng. Mặc dù ví dụ này minh họa một tương tác cực đoan, nhiều nhà thống kê khuyên rằng nên kiểm tra tương tác trước tiên, và nếu nó có ý nghĩa, không nên kiểm tra các hiệu ứng chính.
Bảng 7-9. Các kết quả có thể có cho dữ liệu giả định trong ANOVA hai chiều: Trung bình cho mỗi tổ hợp xử lý.
| Bệnh Alzheimer | Nhóm chứng | |
|---|---|---|
| A. Chênh lệch giữa Bệnh nhân và Nhóm chứng | ||
| Nam | 1.00 | 0.50 |
| Nữ | 1.00 | 0.50 |
| B. Chênh lệch giữa các đối tượng Thừa cân và Cân nặng bình thường | ||
| Bệnh Alzheimer | 0.50 | 1.00 |
| Nhóm chứng | 0.50 | 1.00 |
| C. Chênh lệch chỉ do sự kết hợp của các yếu tố | ||
| Bệnh Alzheimer | 0.50 | 1.00 |
| Nhóm chứng | 1.00 | 0.50 |
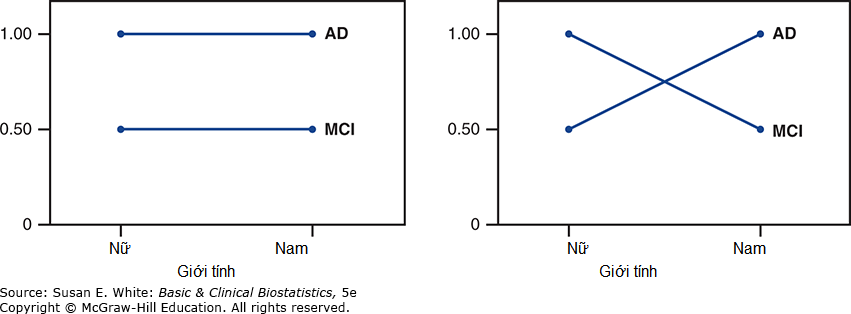
Hình 7-5. Đồ thị của tương tác. A: Không có tương tác; hiệu ứng cộng tính. B: Tương tác có ý nghĩa; hiệu ứng nhân tính.
Các phép tính trong ANOVA hai chiều rất tẻ nhạt và sẽ không được minh họa trong cuốn sách này. Về mặt khái niệm, chúng tương tự như các phép tính trong tình huống một chiều đơn giản hơn; tuy nhiên, tổng biến thiên trong các quan sát được chia ra, và tổng các bình phương được xác định cho yếu tố thứ nhất, yếu tố thứ hai, tương tác của các yếu tố, và sai số (phần dư), tương tự như tổng bình phương trong nhóm trong ANOVA một chiều.
Hãy tham khảo lại Bảng 7-8 để biết các trung bình và độ lệch chuẩn cho mỗi trong bốn nhóm đối tượng riêng lẻ và cho hai nhóm nhận thức và hai giới tính. Trung bình i-ADL-CDI là 0.19 cho các đối tượng mắc MCI và 0.43 cho các đối tượng mắc AD. Đối với phụ nữ, trung bình i-ADL-CDI là 0.34, so với 0.29 đối với nam giới. Khi xem xét các trung bình cho mỗi nhóm riêng lẻ, phụ nữ mắc AD có điểm i-ADL-CDI cao nhất, và các đối tượng nam mắc MCI có điểm số thấp nhất. Phân tích phương sai hai chiều có thể giúp chúng ta hiểu rõ tất cả các trung bình này và xem những trung bình nào khác biệt đáng kể. Kết quả được đưa ra trong Bảng 7-10.
Kết quả máy tính do R tạo ra liệt kê rất nhiều thông tin, nhưng chúng ta tập trung vào các hàng chứa các hiệu ứng chính (DIAGNOSISGROUP và GENDER) và tương tác hai chiều (DIAGNOSISGROUP:GENDER). Chúng ta xem xét hiệu ứng tương tác trước tiên; trung bình bình phương là 0.1395 (MS = SS/df = 0.1395/1), thống kê F là 3.5292, và giá trị p là 0.06238 (trong cột có nhãn Pr(>F)). Vì giá trị p lớn hơn 0.05, Giả thuyết H-Không về không có tương tác không bị bác bỏ, vì vậy chúng ta kết luận không có bằng chứng về tương tác có ý nghĩa giữa mức độ suy giảm nhận thức và giới tính. Một đồ thị của tương tác được đưa ra trong Hình 7-6. Nếu tương tác có ý nghĩa, chúng ta sẽ dừng lại ở điểm này và không tiếp tục diễn giải các hiệu ứng chính của sự suy giảm và giới tính. Tuy nhiên, các đường trong Hình 7-6 không cắt nhau, vì vậy chúng ta có thể xem xét các hiệu ứng chính. Lưu ý rằng đồ thị trong Hình 7-6 chỉ đơn giản là các giá trị trung bình được đưa ra trong Bảng 7-8 cho bốn nhóm riêng lẻ.
Bảng 7-10. Phân tích phương sai cho nghiên cứu i-ADL-CDI.
| Nguồn | Sum Sq | Df | F value | Pr(>F) |
|---|---|---|---|---|
| DIAGNOSISGROUP (NHÓM CHẨN ĐOÁN) | 2.1666 | 1 | 54.7947 | 1.134e-11 *** |
| GIỚI TÍNH (GENDER) | 0.1960 | 1 | 4.9563 | 0.02759 * |
| DIAGNOSISGROUP:GENDER (NHÓM CHẨN ĐOÁN: GIỚI TÍNH) | 0.1395 | 1 | 3.5292 | 0.06238 . |
| Residuals (Còn lại) | 5.5357 | 140 |
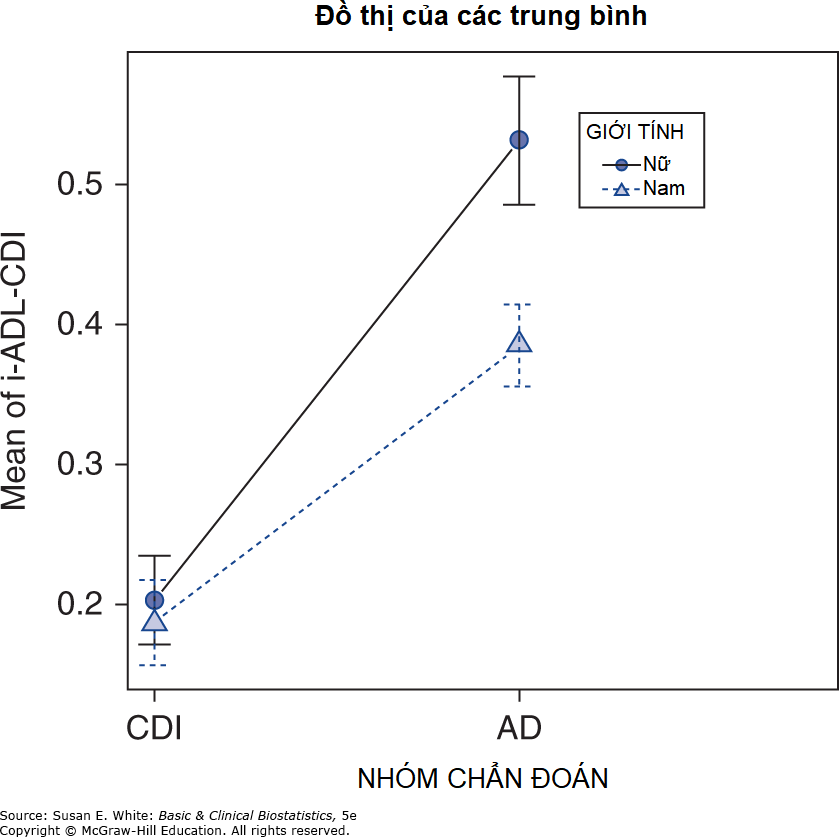
Hình 7-6. Đồ thị tương tác cho nghiên cứu HDL-C.
Hiệu ứng chính của sự suy giảm nhận thức (DIAGNOSISGROUP) có 1 bậc tự do (vì hai nhóm suy giảm đang được phân tích), vì vậy trung bình bình phương giống như tổng các bình phương, 2.1666 trong Bảng 7-10. Thống kê F cho hiệu ứng này là 54.7947, và giá trị p là <0.0001 (1.134e-11 trong ký hiệu khoa học). Do đó, chúng ta bác bỏ Giả thuyết H-Không về trung bình i-ADL-CDI bằng nhau cho hai nhóm được xác định bởi tình trạng suy giảm nhận thức và kết luận rằng các đối tượng mắc AD có điểm i-ADL-CDI cao hơn so với những người mắc MCI. Tương tự, hiệu ứng chính của giới tính là có ý nghĩa, với giá trị p là 0.02, vì vậy chúng ta kết luận rằng giới tính cũng có tác động đến điểm số i-ADL-CDI. Lưu ý rằng điểm i-ADL-CDI cao hơn biểu thị sự suy giảm nhiều hơn.
Thiết kế Giai thừa Ngẫu nhiên
Các nghiên cứu được thảo luận trong chương này cho đến nay là các ví dụ về thiết kế giai thừa ngẫu nhiên với một hoặc hai yếu tố. Các thiết kế giai thừa ngẫu nhiên với ba hoặc nhiều yếu tố cũng có thể thực hiện được, và các ý tưởng được giới thiệu trong phần “ANOVA Hai chiều: Thiết kế Giai thừa” được tổng quát hóa một cách hợp lý. Ví dụ, một nghiên cứu xem xét mức độ suy giảm nhận thức, giới tính, và cân nặng (với nhiều hơn một quan sát cho mỗi tổ hợp xử lý) có tổng các bình phương và trung bình bình phương cho mức độ suy giảm nhận thức, cân nặng, và giới tính; cho các tương tác giữa mức độ suy giảm nhận thức và cân nặng, giữa cân nặng và giới tính, và giữa mức độ suy giảm nhận thức và giới tính; và, cuối cùng, cho tương tác ba chiều giữa cả ba yếu tố. Các nghiên cứu sử dụng nhiều hơn ba hoặc bốn yếu tố rất hiếm trong y học vì số lượng đối tượng cần thiết lớn. Ví dụ, một nghiên cứu với ba yếu tố, mỗi yếu tố có hai mức như chúng ta vừa mô tả, có 2 x 2 x 2 = 8 tổ hợp xử lý; nếu một yếu tố có hai mức, một yếu tố khác có ba mức, và yếu tố thứ ba có bốn mức, thì 2 x 3 x 4 = 24 tổ hợp xử lý khác nhau là có thể. Việc tìm đủ số lượng đối tượng cho mỗi tổ hợp xử lý có thể khó khăn.
Thiết kế Khối Ngẫu nhiên
Một yếu tố được cho là nhiễu (confounded) với một yếu tố khác nếu không thể xác định được yếu tố nào chịu trách nhiệm cho hiệu ứng quan sát được. Tuổi thường là một yếu tố gây nhiễu trong các nghiên cứu y học, vì vậy các nhà điều tra thường ghép cặp đối tượng chứng theo tuổi với các đối tượng điều trị. Thiết kế khối ngẫu nhiên hữu ích khi một yếu tố gây nhiễu góp phần vào sự biến thiên.
Trong thiết kế khối ngẫu nhiên, các đối tượng trước tiên được chia thành các khối đồng nhất; các đối tượng từ mỗi khối sau đó được phân công ngẫu nhiên vào mỗi mức của yếu tố thử nghiệm. Loại nghiên cứu này đặc biệt hữu ích trong các thí nghiệm trong phòng thí nghiệm, nơi các nhà điều tra lo ngại về sự biến đổi di truyền và ảnh hưởng của nó đến kết quả đang được nghiên cứu. Các lứa động vật được xác định là các khối, và các con cùng lứa sau đó được phân công ngẫu nhiên vào các mức xử lý khác nhau. Trong thí nghiệm này, việc phân khối được cho là kiểm soát sự khác biệt di truyền. Trong các nghiên cứu liên quan đến con người, việc phân khối theo tuổi hoặc mức độ nghiêm trọng của một tình trạng thường hữu ích. Đôi khi, các nhà điều tra không thể kiểm soát các yếu tố gây nhiễu có thể có trong thiết kế của một nghiên cứu. Quy trình được gọi là phân tích hiệp phương sai, được thảo luận trong Chương 10, cho phép các nhà điều tra kiểm soát thống kê các yếu tố như vậy trong phân tích.
Thiết kế Hình vuông Latin
Thiết kế hình vuông Latin sử dụng nguyên tắc phân khối cho hai yếu tố gây nhiễu (hoặc yếu tố phiền nhiễu). Các mức của các yếu tố gây nhiễu được gán cho các hàng và các cột của một hình vuông; sau đó, các ô của hình vuông xác định các mức xử lý. Ví dụ, giả sử rằng cả tuổi và cân nặng đều là các yếu tố phân khối quan trọng trong một thí nghiệm có ba mức liều lượng của một loại thuốc làm xử lý. Khi đó, ba khối tuổi và ba khối cân nặng tạo thành một hình vuông Latin với chín ô, và mỗi mức liều lượng xuất hiện một hoặc nhiều lần cho mỗi tổ hợp tuổi-cân nặng. Bảng 7-11 minh họa thiết kế này. Thiết kế hình vuông Latin có thể rất mạnh mẽ, vì chỉ cần chín đối tượng nhưng đã kiểm soát được hai yếu tố gây nhiễu có thể có.
Bảng 7-11. Thiết kế hình vuông Latin với ba mức liều lượng (D1, D2, D3).
| Cân nặng (kg) | <50 tuổi | 50-70 tuổi | >70 tuổi |
|---|---|---|---|
| <60 | D1 | D2 | D3 |
| 60-90 | D2 | D3 | D1 |
| >90 | D3 | D1 | D2 |
Thiết kế Lồng nhau
Trong các thiết kế giai thừa được mô tả trước đây, các yếu tố được chéo nhau, có nghĩa là tất cả các mức của một yếu tố xảy ra trong tất cả các mức của các yếu tố khác. Do đó, tất cả các tổ hợp có thể có đều được bao gồm trong thí nghiệm.
Tuy nhiên, trong một số tình huống, không thể sử dụng các yếu tố chéo nhau; vì vậy, các thiết kế phân cấp, hoặc lồng nhau (hierarchical, or nested) được sử dụng thay thế. Trong các thiết kế phân cấp, một hoặc nhiều xử lý được lồng trong các mức của một yếu tố khác. Việc lồng nhau thường là một sản phẩm của cấu trúc tổ chức. Ví dụ, một giám đốc y tế của bệnh viện có thể muốn so sánh kết quả cho các bệnh nhân trải qua phẫu thuật tim. Một bệnh nhân nhất định thường được phẫu thuật bởi một bác sĩ duy nhất, vì vậy bất kỳ so sánh nào về kết quả đều phụ thuộc vào cả đặc điểm của bệnh nhân và trình độ của bác sĩ. Bệnh nhân được cho là lồng nhau trong các bác sĩ, và không thể xác định được hiệu ứng tương tác giữa đặc điểm của bệnh nhân và trình độ của bác sĩ trừ khi sử dụng các phương pháp đặc biệt, đôi khi được gọi là phương trình ước lượng tổng quát và được thảo luận trong Chương 10.
Thiết kế Đo lường Lặp lại
Hãy nhớ lại từ Chương 5 rằng kiểm định t cặp được sử dụng khi cùng một nhóm đối tượng được quan sát vào hai thời điểm. Thiết kế này rất mạnh mẽ vì nó kiểm soát sự biến thiên cá nhân, vốn có thể lớn trong các nghiên cứu liên quan đến con người. Tương đương với kiểm định t cặp trong ANOVA là thiết kế đo lường lặp lại (hoặc thửa chia nhỏ). Trong thiết kế này, các đối tượng đóng vai trò là nhóm chứng của chính họ, do đó sự biến thiên do khác biệt cá nhân được loại bỏ khỏi sai số (phần dư), làm tăng cơ hội quan sát thấy sự khác biệt có ý nghĩa giữa các mức xử lý. Thiết kế đo lường lặp lại hữu ích trong ba tình huống riêng biệt. Thứ nhất, một nhóm đối tượng được đo lường nhiều hơn hai lần, thường là theo thời gian, chẳng hạn như bệnh nhân được cân tại thời điểm ban đầu và mỗi tháng sau một chương trình giảm cân. Thứ hai, một nhóm đối tượng được đo lường ở nhiều mức của cùng một xử lý, chẳng hạn như bệnh nhân được cho ba liều lượng khác nhau của một loại thuốc. Thứ ba, hai hoặc nhiều nhóm đối tượng được đo lường nhiều hơn một lần, chẳng hạn như nghiên cứu về lưu lượng máu ở các đối tượng đột quỵ của Durand và cs (2015). Trong nghiên cứu này, chân bị liệt và không bị liệt của mười đối tượng sau đột quỵ đã được kiểm tra lưu lượng máu dưới năm điều kiện co cơ của cơ duỗi gối (Nghỉ, 20% co cơ tự nguyện tối đa (MVC), 40% MVC, 60% MVC, và 80% MVC). Các trung bình và độ lệch chuẩn của lưu lượng máu cho mỗi chi ở mỗi mức MVC được đưa ra trong Bảng 7-12. Dữ liệu thô về tất cả các phép đo được công bố cùng với bài báo.
Bảng 7-12. Thống kê tóm tắt lưu lượng máu động mạch đùi cho chi liệt và không liệt ở mỗi mức MVC.
|
Biến số |
Chi không liệt | Chi liệt | Tổng thể |
|---|---|---|---|
| n | 10 | 10 | 20 |
| Trung bình lúc nghỉ | 109.51 | 79.65 | 94.58 |
| ĐL chuẩn lúc nghỉ | 68.68 | 39.69 | 56.70 |
| Trung bình 20% MVC | 160.45 | 100.81 | 130.63 |
| ĐL chuẩn 20% MVC | 92.12 | 48.58 | 77.93 |
| Trung bình 40% MVC | 206.77 | 140.40 | 173.59 |
| ĐL chuẩn 40% MVC | 110.13 | 76.04 | 98.20 |
| Trung bình 60% MVC | 237.23 | 137.06 | 187.14 |
| ĐL chuẩn 60% MVC | 118.12 | 70.39 | 107.69 |
| Trung bình 80% MVC | 264.18 | 162.96 | 213.57 |
| ĐL chuẩn 80% MVC | 135.18 | 85.18 | 121.61 |
Kết quả của một phân tích đo lường lặp lại về lưu lượng máu đùi được đưa ra trong Bảng 7-13. Phép đo được lặp lại, MVC, được gọi là yếu tố trong đối tượng (within-subjects measure); và biến xác định các nhóm khác nhau (liệt so với không liệt) được gọi là yếu tố giữa các đối tượng (between-subjects measure). Quy trình đo lường lặp lại của R rất linh hoạt vì nó có thể sử dụng bất kỳ thiết kế phân tích phương sai nào, nhưng nó cũng khá phức tạp.
Phần của Bảng 7-13 có nhãn “Univariate Type II Repeated-Measures ANOVA Assuming Sphericity” cho thấy có sự khác biệt đáng kể trong MVC, có nghĩa là lưu lượng máu thay đổi theo mức MVC. Mặc dù giá trị p là 0.000 được hiển thị, các tác giả đã báo cáo chính xác là <0.001, vì luôn có khả năng dù là rất nhỏ rằng kết luận là không chính xác.
Bảng 7-13. ANOVA đo lường lặp lại của lưu lượng máu động mạch đùi.
| ANOVA Đo lường lặp lại Loại II đơn biến giả định Tính cầu | |||||
|---|---|---|---|---|---|
| Tổng bình phương | df tử số | SS Sai số | df mẫu số | Giá trị F | |
| (Điểm chặn) | 2556862 | 1 | 612311 | 18 | 75,1637 |
| Bên (Side) | 127631 | 1 | 612311 | 18 | 3,7519 |
| MVC | 178652 | 4 | 103064 | 72 | 31,2014 |
| Bên:MVC | 18032 | 4 | 103064 | 72 | 3,1493 |
| Kiểm tra Mauchly về Tính cầu | Thống kê kiểm định | p-value | |||
| MVC | 0,10348 | 0,000026334 | |||
| Hiệu chỉnh Greenhouse-Geisser (GG) | GG eps | Pr(>F[GG]) | |||
| MVC | 0,53582 | 4,699e-09 *** | |||
| Bên:MVC | 0,53582 | 0,05086 . |
Tập hợp các con số trong Bảng 7-13 ở hàng có nhãn Side:MVC cho thấy kết quả của kiểm định tương tác giữa MVC và bên chi cho thấy giá trị p là 0.01917, nhưng điều này là dưới giả định về tính cầu. Kiểm định tính cầu trong ANOVA đo lường lặp lại tương tự như kiểm định sự bằng nhau của các phương sai trong kiểm định t hai mẫu. Phần trong cùng bảng có nhãn Mauchly Tests for Sphericity cho biết giá trị p của Giả thuyết H-Không là <0.05 và, do đó, chúng ta phải sử dụng một kiểm định hơi khác cho hiệu ứng chính MVC và tương tác của bên chi và MVC bằng cách sử dụng một sự điều chỉnh gọi là Greenhouse-Geisser. Phần cuối cùng trong Bảng 7-13 cho thấy hiệu ứng chính cho MVC vẫn có ý nghĩa (p<0.0001), nhưng giá trị p để kiểm tra tương tác bây giờ là 0.05086, lớn hơn 0.05. Vì tương tác này không có ý nghĩa ở mức 0.05, chúng ta kết luận rằng mô hình thay đổi trong lưu lượng máu đùi không khác nhau đối với hai bên.
Hãy nhớ lại rằng một giả định khác trong ANOVA là các quan sát phải độc lập với nhau. Giả định này thường không được đáp ứng trong ANOVA đo lường lặp lại; do đó, một số giả định khác liên quan đến bản chất phụ thuộc của các quan sát phải được đưa ra và kiểm tra. Mặc dù chúng tôi không thảo luận về những giả định này ở đây, người đọc y văn cần biết rằng ANOVA đo lường lặp lại nên được sử dụng trong các nghiên cứu lặp lại các phép đo trên cùng một đối tượng.
ANOVA PHI THAM SỐ
ANOVA phi tham số không phải là một thiết kế khác mà là một phương pháp phân tích khác. Hãy nhớ lại từ Chương 5 và 6 rằng các phương pháp phi tham số, chẳng hạn như kiểm định tổng hạng Wilcoxon cho hai nhóm độc lập hoặc kiểm định hạng có dấu cho các thiết kế cặp, được sử dụng nếu các giả định cho các kiểm định t bị vi phạm nghiêm trọng. Một tình huống tương tự cũng xảy ra trong ANOVA. Mặc dù kiểm định F mạnh mẽ đối với việc vi phạm giả định về tính chuẩn và, nếu cỡ mẫu bằng nhau, giả định về phương sai bằng nhau, đôi khi nên biến đổi các quan sát sang thang logarit hoặc sử dụng các quy trình phi tham số.
Giống như các quy trình phi tham số được thảo luận trong Chương 5 và 6, các phương pháp phi tham số trong ANOVA dựa trên việc phân tích các hạng của các quan sát thay vì trên các quan sát ban đầu. Đối với ANOVA một chiều, quy trình phi tham số là ANOVA một chiều Kruskal-Wallis theo hạng. Các so sánh post hoc giữa các cặp trung bình có thể được thực hiện bằng cách sử dụng kiểm định tổng hạng Wilcoxon, với việc điều chỉnh giảm mức α để bù trừ cho các so sánh bội, như được mô tả trong phần “So sánh A Priori, hay So sánh có kế hoạch”. Khi có nhiều hơn hai mẫu liên quan được quan tâm, như trong các phép đo lặp lại, quy trình phi tham số được lựa chọn là ANOVA hai chiều Friedman theo hạng. Thuật ngữ “hai” trong ANOVA hai chiều Friedman đề cập đến (1) các mức của yếu tố (hoặc xử lý) và (2) các lần lặp lại mà các đối tượng được quan sát. Như một quy trình theo sau để thực hiện các so sánh cặp, có thể sử dụng kiểm định hạng có dấu Wilcoxon với các bậc tự do được điều chỉnh.
SO SÁNH TẦN SUẤT HOẶC TỶ LỆ Ở NHIỀU HƠN HAI NHÓM
Hãy nhớ lại vấn đề từ Chương 5 nhằm xác định hiệu quả của một quy trình mới để giảm nhiễm trùng khi đặt shunt dịch não tủy của van Lindert và các đồng nghiệp (2018). Chúng ta có thể sử dụng kiểm định z hoặc kiểm định chi-bình phương khi chỉ có hai nhóm được phân tích, nhưng với các bảng tần suất có nhiều hơn hai hàng và hai cột, kiểm định z không còn áp dụng được. Tuy nhiên, chúng ta vẫn có thể sử dụng chi-bình phương, bất kể số lượng mức hoặc loại trong mỗi biến. Bảng 7-14 đưa ra kết quả trong một bảng dự phòng 2 x 3 với phản ứng với quy trình (Không = không nhiễm trùng, Có = nhiễm trùng) là các cột và nhóm tuổi của đối tượng là các hàng.
Bảng 7-14. Minh họa chi-bình phương để so sánh nhiều hơn hai tỷ lệ.
| Nhóm tuổi | Không | Có |
|---|---|---|
| <1 | 47 | 5 |
| 1-17 | 141 | 5 |
| >=17 | 296 | 5 |
Chúng ta sử dụng thống kê chi-bình phương bất kể chúng ta phát biểu câu hỏi nghiên cứu theo tỷ lệ hay tần suất. Ví dụ, van Lindert và các đồng nghiệp có thể hỏi liệu tỷ lệ các đối tượng tránh được nhiễm trùng có giống nhau cho mỗi nhóm tuổi hay không. Hoặc, van Lindert có thể hỏi liệu nhóm tuổi có liên quan đến kết quả nhiễm trùng hay không.
Thống kê chi-bình phương cho dữ liệu của van Lindert trong Bảng 7-14 chính xác là công thức đã được sử dụng trước đây:
ngoại trừ việc các bậc tự do khác nhau. Có sáu số hạng trong công thức cho χ² trong ví dụ này, một cho mỗi trong sáu ô của bảng 2 x 3, vì vậy các bậc tự do là (r-1)(c-1) = (3-1)(2-1) = 2.
Sau đây là các bước tóm tắt cho kiểm định giả thuyết chi-bình phương. Hãy chắc chắn xác nhận các tính toán này bằng R và tệp dữ liệu thô.
Bước 1: H₀: Phản ứng với quy trình độc lập với nhóm tuổi. H₁: Phản ứng với quy trình mới không độc lập với nhóm tuổi.
Bước 2: Kiểm định chi-bình phương phù hợp cho câu hỏi nghiên cứu này vì các quan sát là dữ liệu danh nghĩa (tần suất).
Bước 3: Đối với kiểm định này, chúng ta sử dụng α = 0.05.
Bước 4: Bảng dự phòng có ba hàng và hai cột, vì vậy df = (3-1)(2-1) = 2. Giá trị tới hạn phân tách 1% trên của phân phối χ² khỏi 99% còn lại với 2 df là 9.210 (Bảng A-5). Vì vậy, χ² phải lớn hơn 9.210 để bác bỏ Giả thuyết H-Không về sự độc lập.
Bước 5: Sau khi tính toán các tần suất kỳ vọng cho các ô, chúng ta tính χ²:
χ² = (47-50.44)²/50.44 + (141-141.61)²/141.61 + (296-291.95)²/291.95 + (5-1.56)²/1.56 + (5-4.39)²/4.39 + (5-9.05)²/9.05 = 9.7459
Bước 6: Giá trị quan sát của χ² với 2 df, 9.7459, lớn hơn giá trị tới hạn 9.210, vì vậy chúng ta bác bỏ Giả thuyết H-Không. Chúng ta có thể kết luận rằng phản ứng với quy trình mới có liên quan đến nhóm tuổi. Kết quả từ R được đưa ra trong Bảng 7-15.
Bảng 7-15. Kết quả kiểm định chi-bình phương trên dữ liệu trong Bảng 7-14.
| Phép thử Chi-bình phương của Pearson | |
|---|---|
| Dữ liệu: Bảng | Chi-bình phương = 9,7459, df = 2, p-value = 0,007651 |
| Tần số kỳ vọng: | Không |
| <1 | 50,44 |
| 1-17 | 141,61 |
| >=17 | 291,95 |
| Phép thử chính xác của Fisher cho Dữ liệu đếm | |
| Dữ liệu: Bảng | p-value = 0,01354 |
(Bảng này cho thấy kết quả từ phần mềm R, bao gồm giá trị chi-bình phương, df, giá trị p, và các tần suất kỳ vọng)
Người đọc tinh ý có lẽ đã thắc mắc về số lượng các giá trị kỳ vọng nhỏ trong Bảng 7-15: Hai trong số sáu ô có giá trị kỳ vọng nhỏ hơn 5, và một ô có giá trị kỳ vọng nhỏ hơn 2. Do đó, nên sử dụng chi-bình phương một cách thận trọng vì các giá trị kỳ vọng nhỏ làm cho giá trị của chi-bình phương quá lớn. Trong ví dụ này, Kiểm định Chính xác Fisher có thể được áp dụng như một cách tiếp cận thận trọng. Lưu ý rằng giá trị p cho kiểm định chính xác Fisher là 0.01354; Giả thuyết H-Không về sự độc lập của phản ứng quy trình và nhóm tuổi sẽ không bị bác bỏ ở mức 0.01 khi sử dụng kiểm định này, nhưng sẽ bị bác bỏ ở mức 0.05.
Minh họa trước đó về chi-bình phương chỉ có ba hàng và hai cột, nhưng các bảng dự phòng có thể có bất kỳ số lượng hàng và cột nào. Tất nhiên, cỡ mẫu cần phải tăng lên khi số lượng loại tăng lên để giữ cho các giá trị kỳ vọng ở kích thước chấp nhận được.
Kiểm định chi-bình phương cung cấp một minh họa hay về khái niệm bậc tự do. Giả sử chúng ta có một bảng dự phòng với ba hàng và bốn cột và các tần suất lề, chẳng hạn như Bảng 7-16. Có bao nhiêu ô trong bảng là “tự do biến đổi” (trong các ràng buộc do các tần suất lề áp đặt)?
Bảng 7-16. Minh họa bậc tự do trong chi-bình phương.
| Hàng | Cột 1 | Cột 2 | Cột 3 | Cột 4 | Tổng |
|---|---|---|---|---|---|
| 1 | * | * | * | 75 | |
| 2 | * | * | * | 100 | |
| 3 | 225 | ||||
| Tổng | 100 | 100 | 100 | 100 | 400 |
Trong cột 1, các tần suất cho hàng 1 và 2 có thể có bất kỳ giá trị nào, miễn là không lớn hơn tổng hàng của chúng và tổng của chúng không vượt quá 100, tổng cột 1. Tuy nhiên, tần suất cho hàng 3 được xác định sau khi các tần suất cho hàng 1 và 2 đã được biết; tức là, nó là 100 trừ đi các giá trị ở hàng 1 và 2. Lý luận tương tự áp dụng cho cột 2 và 3. Tuy nhiên, tại thời điểm này, các tần suất ở hàng 3 cũng như tất cả các tần suất ở cột 4 đều được xác định. Do đó, có (3-1) x (4-1) = 2 x 3 = 6 bậc tự do. Nói chung, các bậc tự do cho một bảng dự phòng bằng số hàng trừ 1 nhân với số cột trừ 1, hay, bằng ký hiệu, df = (r-1) x (c-1).
CỠ MẪU CHO ANOVA
Việc xem xét cỡ mẫu cần thiết cho ANOVA cũng quan trọng như khi chỉ nghiên cứu một hoặc hai nhóm. Thật không may, các quy trình trong các chương trình phân tích công suất không đơn giản để sử dụng như các quy trình cho trung bình và tỷ lệ. Như đã lưu ý nhiều lần trong chương này, nếu bạn đang lên kế hoạch cho một nghiên cứu mà ANOVA là phù hợp, việc gặp một nhà thống kê trước khi bắt đầu là một ý tưởng tốt.
Chúng tôi đã sử dụng chương trình GPower để tìm cỡ mẫu ước tính cho nghiên cứu của Dysangco và cs (2017). Chúng tôi đã sử dụng các kết quả quan sát được cho HCL-C (mg/dL) để xác định số lượng trong mỗi nhóm cần thiết cho công suất 80%. GPower yêu cầu kích thước hiệu ứng mong muốn để xác định cỡ mẫu. Trong trường hợp này, chúng tôi giả định rằng chúng tôi muốn phát hiện một kích thước hiệu ứng trung bình (0.25) với ba nhóm, công suất 80% và alpha là 0.05. Tổng cỡ mẫu cần thiết là 159. Xem Hình 7-7 để biết kết quả tính toán công suất.
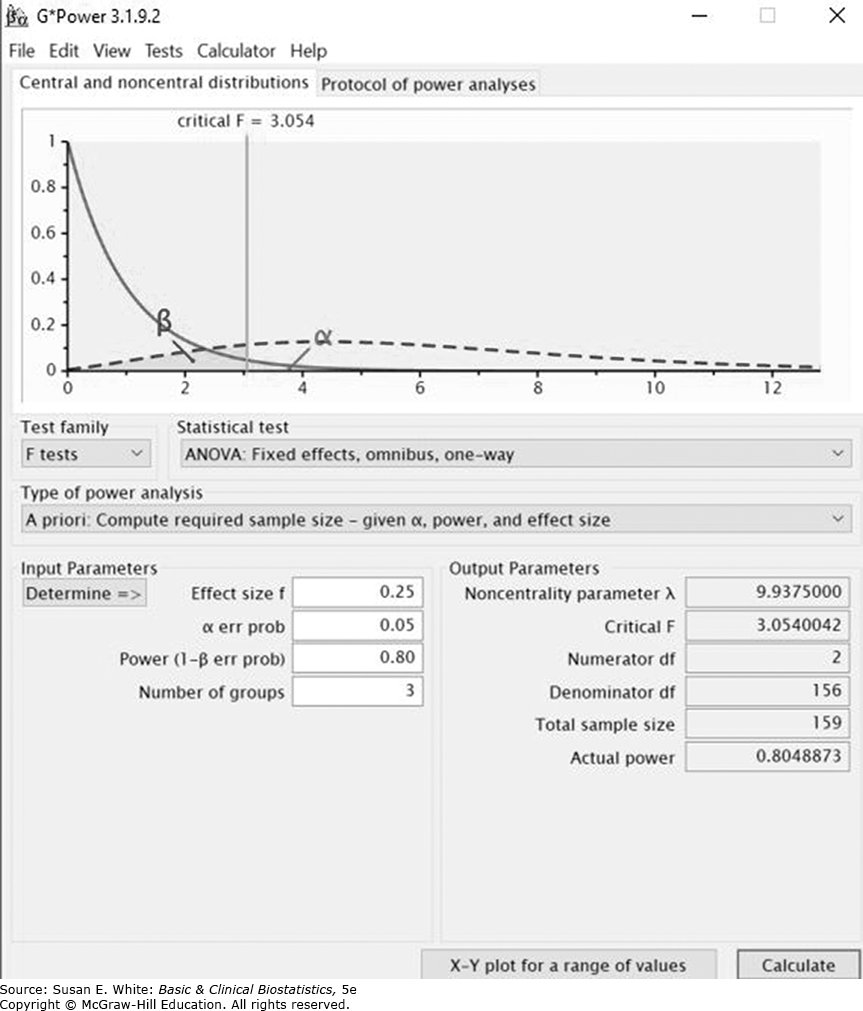
Hình 7-7. Kết quả từ chương trình G*Power ước tính cỡ mẫu cho ANOVA một chiều.
TÓM TẮT
Trong nghiên cứu được mô tả trong Vấn đề tình huống 1, van Lindert đã phân tích dữ liệu cho HDL-C bằng cách sử dụng phân tích phương sai một chiều và theo sau các phát hiện có ý nghĩa bằng hiệu chỉnh Bonferroni/Dunn cho các so sánh bội.
Nghiên cứu của ông đã đánh giá ảnh hưởng của HIV và ART đến nồng độ HDL-C. Ông đã thực hiện một phân tích hồi cứu trên ba nhóm bệnh nhân: HIV+ không có ART, HIV+ có ART và nhóm chứng HIV-. Van Lindert thấy rằng nồng độ HDL-C thấp hơn ở cả hai nhóm HIV+ so với nhóm chứng.
Cornelis và các đồng nghiệp (2017) đã tìm thấy sự khác biệt đáng kể trong một thang đo tổng hợp về các hoạt động sinh hoạt hàng ngày ở các đối tượng mắc bệnh Alzheimer và các đối tượng bị suy giảm nhận thức nhẹ. Chúng tôi đã xác nhận các phát hiện cho i-ADL-CDI bằng cách sử dụng phân tích phương sai hai chiều. Các nhà điều tra cũng báo cáo rằng, không có tương tác đáng kể giữa giới tính của đối tượng và mức độ suy giảm của họ đối với mức độ chức năng ADL của họ.
Dữ liệu từ nghiên cứu của Durand và các đồng nghiệp (2015) đã được sử dụng để minh họa phân tích phương sai đo lường lặp lại. Họ đã tìm thấy những thay đổi đáng kể trong lưu lượng động mạch đùi khi mức độ co cơ thay đổi. Cũng có một hiệu ứng nhóm đáng kể—bên bị liệt so với bên không bị liệt.
Việc xác định thiết kế nghiên cứu ANOVA nào là phù hợp nhất cho một cuộc điều tra nhất định thường khó khăn. Việc đưa ra quyết định này đòi hỏi kiến thức về lĩnh vực đang được điều tra và về các phương pháp thiết kế thực nghiệm. Các cân nhắc phải bao gồm loại dữ liệu sẽ được thu thập (danh nghĩa, thứ bậc, khoảng), số lượng các phương pháp điều trị sẽ được bao gồm và liệu việc có được các ước tính về hiệu ứng tương tác có quan trọng hay không, số lượng các mức xử lý sẽ được bao gồm và liệu chúng nên là cố định hay ngẫu nhiên, khả năng phân khối trên các yếu tố gây nhiễu, số lượng đối tượng cần thiết và liệu con số đó có đủ cho các thiết kế được đề xuất hay không, và các hệ quả của việc vi phạm các giả định trong ANOVA. Mặc dù Sơ đồ C-2 trong Phụ lục C đưa ra một số hướng dẫn cho các thiết kế cơ bản, việc lựa chọn thiết kế tốt nhất đòi hỏi sự giao tiếp giữa các nhà điều tra và các nhà thống kê, và thiết kế tốt nhất có thể là không thể thực hiện được vì một hoặc nhiều trong số các cân nhắc vừa được liệt kê.
Mặc dù tất cả các quy trình post hoc được mô tả trong phần “Các Quy trình So sánh Bội” đều được sử dụng trong nghiên cứu y tế, một số phương pháp tốt hơn những phương pháp khác cho các thiết kế nghiên cứu cụ thể. Đối với các so sánh cặp (giữa các cặp trung bình), kiểm định của Tukey là lựa chọn hàng đầu và quy trình Newman-Keuls là lựa chọn thứ hai. Khi một số trung bình điều trị cần được so sánh với một trung bình chứng duy nhất nhưng không có so sánh nào giữa các phương pháp điều trị được mong muốn, quy trình của Dunnett là tốt nhất. Đối với các so sánh không phải là cặp, chẳng hạn như [(μ₁ + μ₂)/2] – μ₃, quy trình của Scheffé là tốt nhất. Kiểm định phạm vi bội mới của Duncan và kiểm định khác biệt có ý nghĩa nhỏ nhất không được khuyến nghị.
Người đọc y văn có thể gặp khó khăn trong việc đánh giá liệu thiết kế tốt nhất đã được sử dụng trong một nghiên cứu hay chưa. Các tác giả của các bài báo trên tạp chí không phải lúc nào cũng cung cấp đủ chi tiết về thiết kế thực nghiệm, và có thể không thể biết được những hạn chế hiện có khi nghiên cứu được thiết kế. Trong những tình huống này, người đọc chỉ có thể đánh giá danh tiếng của các tác giả và các tổ chức liên kết của họ và đánh giá các thực hành học thuật của tạp chí mà nghiên cứu được xuất bản. Các tạp chí ngày càng yêu cầu các tác giả chỉ định thiết kế nghiên cứu và phương pháp phân tích của họ, và chúng tôi hy vọng họ sẽ tiếp tục nỗ lực của mình.
BÀI TẬP THỰC HÀNH
1. Sử dụng dữ liệu từ Dysangco và cs (2017) để thực hiện ANOVA một chiều cho IL-6, sử dụng α=0.05. Diễn giải kết quả phân tích của bạn. Bạn có thể sử dụng công thức rút gọn và dữ liệu trong Bảng 7-1 hoặc dữ liệu thô.
2. Sử dụng dữ liệu từ Dysangco và cs để thực hiện kiểm định HSD của Tukey và quy trình post hoc của Scheffé để so sánh ba trung bình của ADMA; bạn cũng có thể chạy quy trình này với chương trình ANOVA một chiều trong SPSS hoặc R. So sánh các kết luận được rút ra với hai quy trình này.
3. Một nghiên cứu đã được thực hiện để so sánh việc sử dụng thuốc của các bác sĩ, dược sĩ, sinh viên y khoa và sinh viên dược. Các bộ so sánh sau đây là độc lập hay phụ thuộc?
a. Bác sĩ với dược sĩ và sinh viên y khoa với sinh viên dược
b. Sinh viên y khoa với bác sĩ và bác sĩ với dược sĩ
c. Sinh viên y khoa với bác sĩ và dược sĩ với sinh viên dược
d. Sinh viên y khoa với bác sĩ, sinh viên y khoa với dược sĩ, và sinh viên y khoa với sinh viên dược.
4. Các nhà nghiên cứu y học quan tâm đến mối quan hệ giữa việc sử dụng rượu cùng với các đặc điểm lối sống khác và sự phát triển của các bệnh, chẳng hạn như ung thư và tăng huyết áp. Dữ liệu giả định trong Bảng 7-17 có thể là kết quả từ một ANOVA trong một nghiên cứu so sánh huyết áp trung bình của các bệnh nhân tiêu thụ các lượng rượu khác nhau.
a. Loại ANOVA nào được biểu diễn trong Bảng 7-17?
b. Tổng biến thiên là bao nhiêu?
c. Có bao nhiêu nhóm bệnh nhân trong nghiên cứu? Có bao nhiêu bệnh nhân trong nghiên cứu?
d. Giá trị của tỷ số F là bao nhiêu?
e. Giá trị tới hạn ở mức 0.01 là bao nhiêu?
f. Kết luận nào là phù hợp?
Bảng 7-17. ANOVA về huyết áp trung bình.
| Nguồn biến thiên |
Tổng bình phương |
df | Trung bình bình phương | F |
|---|---|---|---|---|
| Giữa các nhóm | 800 | 3 | ||
| Trong các nhóm | 1,200 | 36 |
33.3 |
|
| Tổng |
|
5. Bệnh vẩy nến là một rối loạn da viêm mãn tính đặc trưng bởi các mảng da có vảy, ban đỏ. Nó có thể bắt đầu ở mọi lứa tuổi, thường liên quan đến móng tay và móng chân, và đi kèm với viêm khớp ở 5-10% bệnh nhân. Có một ảnh hưởng di truyền mạnh mẽ—khoảng một phần ba bệnh nhân có tiền sử gia đình dương tính, và các nghiên cứu trên cặp song sinh cho thấy tỷ lệ tương hợp cao hơn ở các cặp song sinh cùng trứng so với các cặp song sinh khác trứng hoặc anh chị em (70% so với 23%). Stuart và các đồng nghiệp (2002) đã tiến hành một nghiên cứu để xác định xem có bất kỳ sự khác biệt nào về biểu hiện lâm sàng giữa các bệnh nhân có tiền sử gia đình dương tính và âm tính với bệnh vẩy nến và với bệnh khởi phát sớm so với khởi phát muộn. Nhóm nghiên cứu bao gồm 537 cá nhân được chọn ngẫu nhiên từ một quần thể những người mắc bệnh vẩy nến được đánh giá tại Đại học Michigan. Ở 227 cá nhân, không có tiền sử gia đình nào được biết đến về bệnh vẩy nến và những người này đại diện cho nhóm bệnh vẩy nến lẻ tẻ. Nhóm bệnh vẩy nến gia đình bao gồm 310 cá nhân trong đó bệnh vẩy nến được báo cáo ở ít nhất một người thân cấp một. Bệnh vẩy nến khởi phát sớm được định nghĩa là tuổi chẩn đoán từ 40 tuổi trở xuống. Các thước đo mức độ nghiêm trọng của bệnh bao gồm phần trăm diện tích bề mặt cơ thể bị ảnh hưởng (%TBSA), thay đổi ở móng, và sự hiện diện hoặc vắng mặt của các triệu chứng khớp. Kết quả của ANOVA được đưa ra trong Bảng 7-18.
a. Có sự khác biệt về %TBSA liên quan đến tuổi khởi phát không?
b. Có sự khác biệt về %TBSA liên quan đến loại bệnh vẩy nến (gia đình so với lẻ tẻ) không?
c. Tương tác có ý nghĩa không? d. Kết luận của bạn là gì?
Bảng 7-18. Bảng phân tích phương sai.
| Nguồn biến thiên | Tổng bình phương | Bậc tự do | Trung bình bình phương | F | p Phân phối F | p Ngẫu nhiên hóa |
|---|---|---|---|---|---|---|
|
Khởi phát |
0.472 | 1 | 0.472 | 0.37 | 0.545 | 0.547 |
| Gia đình | 25.99 | 1 | 25.99 | 20.22 | 8.49 x 10⁻⁶ | 1.00 x 10⁻⁵ |
| Tương tác | 26.96 | 1 | 26.96 | 20.98 | 5.80 x 10⁻⁶ | 1.00 x 10⁻⁵ |
|
Sai số |
685.1 | 533 | 1.285 |
|
Bảng chú giải thuật ngữ Thống kê Anh-Việt (Chương 7)
| STT | Thuật ngữ tiếng Anh | Phiên âm IPA | Nghĩa Tiếng Việt |
|---|---|---|---|
| 1 | Means | /miːnz/ | Các giá trị trung bình |
| 2 | Groups | /ɡruːps/ | Các nhóm |
| 3 | Statistical tests | /stəˈtɪstɪkəl tɛsts/ | Các kiểm định thống kê |
| 4 | Variables | /ˈvɛəriəblz/ | Các biến số |
| 5 | Analysis of variance (ANOVA) | /əˈnælɪsɪs əv ˈvɛəriəns/ | Phân tích phương sai |
| 6 | Variance | /ˈvɛəriəns/ | Phương sai |
| 7 | Observation | /ˌɒbzəˈveɪʃən/ | Quan sát |
| 8 | Within-group | /wɪðˈɪn ɡruːp/ | (Trong) nội nhóm |
| 9 | Error variance | /ˈɛrə ˈvɛəriəns/ | Phương sai sai số |
| 10 | F test | /ɛf tɛst/ | Kiểm định F |
| 11 | Definitional formulas | /ˌdɛfɪˈnɪʃənl ˈfɔːmjuləz/ | Các công thức định nghĩa |
| 12 | Bonferroni procedure | /ˌbɒnfəˈroʊni prəˈsiːdʒər/ | Quy trình Bonferroni |
| 13 | Multiple comparison | /ˈmʌltɪpl kəmˈpærɪsən/ | So sánh bội |
| 14 | Post hoc | /poʊst hɒk/ | Hậu nghiệm |
| 15 | Tukey’s test | /ˈtuːkiz tɛst/ | Kiểm định Tukey |
| 16 | Mean differences | /miːn ˈdɪfrənsɪz/ | Các chênh lệch trung bình |
| 17 | Scheffé post hoc procedure | /ʃɛˈfeɪ poʊst hɒk prəˈsiːdʒər/ | Quy trình post hoc Scheffé |
| 18 | Conservative | /kənˈsɜːvətɪv/ | (Tính) bảo thủ, chặt chẽ |
| 19 | Versatile | /ˈvɜːsətaɪl/ | Linh hoạt |
| 20 | Newman-Kuels procedure | /ˈnjuːmən kɔɪlz prəˈsiːdʒər/ | Quy trình Newman-Kuels |
| 21 | Dunnett’s procedure | /dəˈnɛts prəˈsiːdʒər/ | Quy trình Dunnett |
| 22 | Control group | /kənˈtroʊl ɡruːp/ | Nhóm chứng |
| 23 | One-way ANOVA | /wʌn weɪ əˈnoʊvə/ | ANOVA một chiều |
| 24 | Assumptions | /əˈsʌmpʃənz/ | Các giả định |
| 25 | Type I error | /taɪp wʌn ˈɛrər/ | Sai lầm loại I |
| 26 | Two-way ANOVA | /tuː weɪ əˈnoʊvə/ | ANOVA hai chiều |
| 27 | Factor | /ˈfæktər/ | Yếu tố |
| 28 | Interaction | /ˌɪntərˈækʃən/ | Tương tác |
| 29 | Factorial designs | /fækˈtɔːriəl dɪˈzaɪnz/ | Thiết kế giai thừa |
| 30 | Confounding variables | /kənˈfaʊndɪŋ ˈvɛəriəblz/ | Các biến gây nhiễu |
| 31 | Randomized block design | /ˈrændəmaɪzd blɒk dɪˈzaɪn/ | Thiết kế khối ngẫu nhiên |
| 32 | Repeated-measures ANOVA | /rɪˈpiːtɪd ˈmɛʒərz əˈnoʊvə/ | ANOVA đo lường lặp lại |
| 33 | Paired t-test | /pɛərd tiː tɛst/ | Kiểm định t cặp |
| 34 | Split-plot design | /splɪt plɒt dɪˈzaɪn/ | Thiết kế thửa chia nhỏ |
| 35 | Nonparametric | /ˌnɒnpærəˈmɛtrɪk/ | Phi tham số |
| 36 | Kruskal-Wallis test | /ˈkrʌskəl ˈwɒlɪs tɛst/ | Kiểm định Kruskal-Wallis |
| 37 | Friedman two-way ANOVA | /ˈfriːdmən tuː weɪ əˈnoʊvə/ | ANOVA hai chiều Friedman |
| 38 | Wilcoxon procedures | /wɪlˈkɒksən prəˈsiːdʒərz/ | Các quy trình Wilcoxon |
| 39 | Chi-square test | /kaɪ skwɛər tɛst/ | Kiểm định chi-bình phương |
| 40 | Proportions | /prəˈpɔːʃənz/ | Các tỷ lệ |
| 41 | Power analysis | /ˈpaʊər əˈnælɪsɪs/ | Phân tích công suất (độ mạnh) |
| 42 | HIV infections | /ˌeɪtʃ aɪ ˈviː ɪnˈfɛkʃənz/ | Nhiễm HIV |
| 43 | Cardiovascular disease | /ˌkɑːdiəʊˈvæskjələr dɪˈziːz/ | Bệnh tim mạch |
| 44 | Biomarkers | /ˈbaɪəʊˌmɑːkərz/ | Các dấu ấn sinh học |
| 45 | Antiretroviral therapy (ART) | /ˌæntirɛtroʊˈvaɪərəl ˈθɛrəpi/ | Liệu pháp kháng retrovirus |
| 46 | Healthy controls | /ˈhɛlθi kənˈtroʊlz/ | Nhóm chứng khỏe mạnh |
| 47 | Endothelial function | /ˌɛndoʊˈθiːliəl ˈfʌŋkʃən/ | Chức năng nội mô |
| 48 | Inflammation | /ˌɪnfləˈmeɪʃən/ | Viêm |
| 49 | Metabolism | /məˈtæbəlɪzəm/ | Chuyển hóa |
| 50 | Oxidative stress | /ˈɒksɪdətɪv strɛs/ | Stress oxy hóa |
| 51 | Cognitive impairment | /ˈkɒɡnətɪv ɪmˈpɛəmənt/ | Suy giảm nhận thức |
| 52 | Activities of daily living (ADL) | /ækˈtɪvətiz əv ˈdeɪli ˈlɪvɪŋ/ | Các hoạt động sinh hoạt hàng ngày |
| 53 | Alzheimer’s Disease | /ˈæltshaɪmərz dɪˈziːz/ | Bệnh Alzheimer |
| 54 | Mild cognitive impairment (MCI) | /maɪld ˈkɒɡnətɪv ɪmˈpɛəmənt/ | Suy giảm nhận thức nhẹ |
| 55 | Stroke | /stroʊk/ | Đột quỵ |
| 56 | Paretic | /pəˈrɛtɪk/ | (Bị) liệt nhẹ |
| 57 | Nonparetic | /nɒnpəˈrɛtɪk/ | Không bị liệt nhẹ |
| 58 | Ultrasound | /ˈʌltrəsaʊnd/ | Siêu âm |
| 59 | Maximum voluntary contraction (MVC) | /ˈmæksɪməm ˈvɒləntəri kənˈtrækʃən/ | Co cơ tự nguyện tối đa |
| 60 | Categorical measure | /ˌkætɪˈɡɒrɪkəl ˈmɛʒər/ | Thước đo định tính |
| 61 | Numerical outcome | /njuːˈmɛrɪkəl ˈaʊtkʌm/ | Kết quả dạng số |
| 62 | Omnibus test | /ˈɒmnɪbəs tɛst/ | Kiểm định tổng thể |
| 63 | Significance level | /sɪɡˈnɪfɪkəns ˈlɛvl/ | Mức ý nghĩa |
| 64 | Myocardial perfusion imaging | /ˌmaɪəʊˈkɑːdiəl pəˈfjuːʒən ˈɪmɪdʒɪŋ/ | Chụp ảnh tưới máu cơ tim |
| 65 | Coronary vessels | /ˈkɒrənəri ˈvɛsəlz/ | Các mạch vành |
| 66 | High-density lipoprotein cholesterol (HDL-C) | /haɪ ˈdɛnsəti ˌlaɪpoʊˈproʊtiːn kəˈlɛstərɒl/ | Cholesterol lipoprotein tỷ trọng cao |
| 67 | Asymmetric dimethylarginine (ADMA) | /ˌeɪsɪˈmɛtrɪk daɪˌmɛθɪlˈɑːdʒɪniːn/ | Asymmetric dimethylarginine |
| 68 | Interleukin 6 (IL-6) | /ˌɪntəˈluːkɪn sɪks/ | Interleukin 6 |
| 69 | Grand mean | /ɡrænd miːn/ | Trung bình chung |
| 70 | Squared deviation | /skwɛərd ˌdiːviˈeɪʃən/ | Độ lệch bình phương |
| 71 | Mean square among groups | /miːn skwɛər əˈmʌŋ ɡruːps/ | Trung bình bình phương giữa các nhóm |
| 72 | Error mean square | /ˈɛrə miːn skwɛər/ | Trung bình bình phương sai số |
| 73 | Null hypothesis | /nʌl haɪˈpɒθəsɪs/ | Giả thuyết H-Không (giả thuyết null, Giả thuyết H0) |
| 74 | Alternative hypothesis | /ɔːlˈtɜːnətɪv haɪˈpɒθəsɪs/ | Giả thuyết đối |
| 75 | Test statistic | /tɛst stəˈtɪstɪk/ | Thống kê kiểm định |
| 76 | Degrees of freedom | /dɪˈɡriːz əv ˈfriːdəm/ | Bậc tự do |
| 77 | Critical value | /ˈkrɪtɪkəl ˈvæljuː/ | Giá trị tới hạn |
| 78 | Rejection area | /rɪˈdʒɛkʃən ˈɛəriə/ | Miền bác bỏ |
| 79 | Dependent variable | /dɪˈpɛndənt ˈvɛəriəbl/ | Biến phụ thuộc |
| 80 | Independent variable | /ˌɪndɪˈpɛndənt ˈvɛəriəbl/ | Biến độc lập |
| 81 | Sums of squares (SS) | /sʌmz əv skwɛərz/ | Tổng bình phương |
| 82 | Levels | /ˈlɛvlz/ | Các mức |
| 83 | Treatments | /ˈtriːtmənts/ | Các phương pháp điều trị |
| 84 | Fixed-effects model | /fɪkst ɪˈfɛkts ˈmɒdl/ | Mô hình hiệu ứng cố định |
| 85 | Random-effects model | /ˈrændəm ɪˈfɛkts ˈmɒdl/ | Mô hình hiệu ứng ngẫu nhiên |
| 86 | Residual | /rɪˈzɪdjuəl/ | Phần dư |
| 87 | Total sum of squares (SST) | /ˈtoʊtl sʌm əv skwɛərz/ | Tổng bình phương toàn bộ |
| 88 | Error sum of squares (SSE) | /ˈɛrə sʌm əv skwɛərz/ | Tổng bình phương sai số |
| 89 | Sum of squares among groups (SSA) | /sʌm əv skwɛərz əˈmʌŋ ɡruːps/ | Tổng bình phương giữa các nhóm |
| 90 | Computational formulas | /ˌkɒmpjuˈteɪʃənl ˈfɔːmjuləz/ | Các công thức tính toán |
| 91 | Round-off error | /raʊnd ɒf ˈɛrər/ | Sai số làm tròn |
| 92 | Normality | /nɔːˈmæləti/ | (Tính) phân phối chuẩn |
| 93 | Homogeneity of variances | /ˌhɒmədʒəˈniːəti əv ˈvɛəriənsɪz/ | Tính đồng nhất của các phương sai |
| 94 | Robust | /roʊˈbʌst/ | (Tính) mạnh, vững |
| 95 | Skewed | /skjuːd/ | (Bị) lệch |
| 96 | Transformation | /ˌtrænsfəˈmeɪʃən/ | Phép biến đổi (dữ liệu) |
| 97 | A priori comparisons | /ˌeɪ praɪˈɔːri kəmˈpærɪsənz/ | Các so sánh tiên nghiệm |
| 98 | Posteriori comparisons | /ˌpoʊstɪəriˈɔːri kəmˈpærɪsənz/ | Các so sánh hậu nghiệm |
| 99 | Contrast | /ˈkɒntræst/ | Tương phản |
| 100 | Orthogonal | /ɔːˈθɒɡənl/ | Trực giao |
| 101 | Pairwise comparisons | /ˈpɛəwaɪz kəmˈpærɪsənz/ | Các so sánh cặp |
| 102 | Dunn’s multiple-comparison | /dʌnz ˈmʌltɪpl kəmˈpærɪsən/ | So sánh bội của Dunn |
| 103 | Honestly significant difference (HSD) | /ˈɒnɪstli sɪɡˈnɪfɪkənt ˈdɪfrəns/ | Khác biệt có ý nghĩa trung thực |
| 104 | Studentized range | /ˈstjuːdəntaɪzd reɪndʒ/ | Dải student hóa |
| 105 | Confidence interval | /ˈkɒnfɪdəns ˈɪntəvəl/ | Khoảng tin cậy |
| 106 | Stepwise approach | /ˈstɛpwaɪz əˈproʊtʃ/ | Phương pháp tiếp cận từng bước |
| 107 | Duncan’s new multiple-range test | /ˈdʌŋkənz njuː ˈmʌltɪpl reɪndʒ tɛst/ | Kiểm định phạm vi bội mới của Duncan |
| 108 | Least significant difference (LSD) | /liːst sɪɡˈnɪfɪkənt ˈdɪfrəns/ | Khác biệt có ý nghĩa nhỏ nhất |
| 109 | Randomized assignment | /ˈrændəmaɪzd əˈsaɪnmənt/ | Phân công ngẫu nhiên |
| 110 | Crossed factors | /krɒst ˈfæktərz/ | Các yếu tố chéo nhau |
| 111 | Main effect | /meɪn ɪˈfɛkt/ | Hiệu ứng chính |
| 112 | Additive effects | /ˈædətɪv ɪˈfɛkts/ | Các hiệu ứng cộng tính |
| 113 | Multiplicative effects | /ˌmʌltɪˈplɪkətɪv ɪˈfɛkts/ | Các hiệu ứng nhân tính |
| 114 | Confounded | /kənˈfaʊndɪd/ | (Bị) nhiễu, lẫn lộn |
| 115 | Latin square designs | /ˈlætɪn skwɛər dɪˈzaɪnz/ | Thiết kế hình vuông Latin |
| 116 | Nuisance factors | /ˈnjuːsns ˈfæktərz/ | Các yếu tố phiền nhiễu |
| 117 | Hierarchical designs | /ˌhaɪəˈrɑːkɪkəl dɪˈzaɪnz/ | Thiết kế phân cấp |
| 118 | Nested designs | /ˈnɛstɪd dɪˈzaɪnz/ | Thiết kế lồng nhau |
| 119 | Within-subjects measure | /wɪðˈɪn ˈsʌbdʒɪkts ˈmɛʒər/ | Thước đo trong đối tượng |
| 120 | Between-subjects measure | /bɪˈtwiːn ˈsʌbdʒɪkts ˈmɛʒər/ | Thước đo giữa các đối tượng |
| 121 | Sphericity | /sfɪˈrɪsəti/ | Tính cầu |
| 122 | Mauchly’s Test | /ˈmɔːkliz tɛst/ | Kiểm định Mauchly |
| 123 | Greenhouse-Geisser correction | /ˈɡriːnhaʊs ˈɡaɪsər kəˈrɛkʃən/ | Hiệu chỉnh Greenhouse-Geisser |
| 124 | Frequency table | /ˈfriːkwənsi ˈteɪbl/ | Bảng tần suất |
| 125 | Contingency table | /kənˈtɪndʒənsi ˈteɪbl/ | Bảng dự phòng (bảng chéo) |
| 126 | Expected frequencies | /ɪkˈspɛktɪd ˈfriːkwənsiz/ | Các tần suất kỳ vọng |
| 127 | Fisher’s Exact Test | /ˈfɪʃərz ɪɡˈzækt tɛst/ | Kiểm định chính xác Fisher |
| 128 | Marginal frequencies | /ˈmɑːdʒɪnl ˈfriːkwənsiz/ | Các tần suất lề |
| 129 | Effect size | /ɪˈfɛkt saɪz/ | Kích thước hiệu ứng |
| 130 | Retrospective analysis | /ˌrɛtrəˈspɛktɪv əˈnælɪsɪs/ | Phân tích hồi cứu |
| 131 | Psoriasis | /səˈraɪəsɪs/ | Bệnh vẩy nến |
| 132 | Inflammatory skin disorder | /ɪnˈflæmətəri skɪn dɪsˈɔːdər/ | Rối loạn viêm da |
| 133 | Erythematous patches | /ˌɛrɪˈθiːmətəs ˈpætʃɪz/ | Các mảng ban đỏ |
| 134 | Plaques | /plæks/ | Các mảng (da) |
| 135 | Joint inflammation | /dʒɔɪnt ˌɪnfləˈmeɪʃən/ | Viêm khớp |
| 136 | Family history | /ˈfæməli ˈhɪstəri/ | Tiền sử gia đình |
| 137 | Concordance rate | /kənˈkɔːdəns reɪt/ | Tỷ lệ tương hợp |
| 138 | Monozygotic twins | /ˌmɒnoʊzaɪˈɡɒtɪk twɪnz/ | Song sinh cùng trứng |
| 139 | Dizygotic twins | /ˌdaɪzaɪˈɡɒtɪk twɪnz/ | Song sinh khác trứng |
| 140 | Siblings | /ˈsɪblɪŋz/ | Anh chị em ruột |
| 141 | Clinical manifestations | /ˈklɪnɪkəl ˌmænɪfɛˈsteɪʃənz/ | Các biểu hiện lâm sàng |
| 142 | Early-onset | /ˈɜːli ˈɒnsɛt/ | Khởi phát sớm |
| 143 | Late-onset | /leɪt ˈɒnsɛt/ | Khởi phát muộn |
| 144 | Disease severity | /dɪˈziːz sɪˈvɛrəti/ | Mức độ nghiêm trọng của bệnh |
| 145 | Body surface area (%TBSA) | /ˈbɒdi ˈsɜːfɪs ˈɛəriə/ | Diện tích bề mặt cơ thể |
| 146 | Nail changes | /neɪl ˈtʃeɪndʒɪz/ | Các thay đổi ở móng |
| 147 | Joint symptoms | /dʒɔɪnt ˈsɪmptəmz/ | Các triệu chứng ở khớp |
| 148 | Sporadic psoriasis | /spəˈrædɪk səˈraɪəsɪs/ | Bệnh vẩy nến lẻ tẻ |
| 149 | Familial psoriasis | /fəˈmɪliəl səˈraɪəsɪs/ | Bệnh vẩy nến gia đình |
| 150 | First-degree relative | /fɜːst dɪˈɡriː ˈrɛlətɪv/ | Người thân cấp một |
| 151 | Phenotypic variation | /ˌfiːnoʊˈtɪpɪk ˌvɛəriˈeɪʃən/ | Biến dị kiểu hình |
| 152 | Randomization | /ˌrændəmaɪˈzeɪʃən/ | Sự ngẫu nhiên hóa |
| 153 | Blood flow | /blʌd floʊ/ | Lưu lượng máu |
| 154 | Knee extensor | /niː ɪkˈstɛnsər/ | Cơ duỗi gối |
| 155 | Femoral artery | /ˈfɛmərəl ˈɑːtəri/ | Động mạch đùi |
| 156 | Drug use | /drʌɡ juːs/ | Việc sử dụng thuốc |
| 157 | Physicians | /fɪˈzɪʃənz/ | Các bác sĩ |
| 158 | Pharmacists | /ˈfɑːməsɪsts/ | Các dược sĩ |
| 159 | Medical students | /ˈmɛdɪkəl ˈstjuːdənts/ | Sinh viên y khoa |
| 160 | Pharmacy students | /ˈfɑːməsi ˈstjuːdənts/ | Sinh viên dược |
| 161 | Hypertension | /ˌhaɪpəˈtɛnʃən/ | Tăng huyết áp |
| 162 | Alcohol use | /ˈælkəhɒl juːs/ | Việc sử dụng rượu |
| 163 | Blood pressure | /blʌd ˈprɛʃər/ | Huyết áp |
| 164 | Total variation | /ˈtoʊtl ˌvɛəriˈeɪʃən/ | Tổng biến thiên |
| 165 | Population variance | /ˌpɒpjuˈleɪʃən ˈvɛəriəns/ | Phương sai tổng thể |
| 166 | Sample size | /ˈsɑːmpl saɪz/ | Cỡ mẫu |
| 167 | Statistical software | /stəˈtɪstɪkəl ˈsɒftwɛər/ | Phần mềm thống kê |
| 168 | Familywise confidence intervals | /ˈfæməliwaɪz ˈkɒnfɪdəns ˈɪntəvəlz/ | Các khoảng tin cậy đồng thời |
| 169 | Linear function | /ˈlɪniər ˈfʌŋkʃən/ | Hàm tuyến tính |
| 170 | Diagnosis group | /ˌdaɪəɡˈnoʊsɪs ɡruːp/ | Nhóm chẩn đoán |
| 171 | Residuals | /rɪˈzɪdjuəlz/ | Các phần dư |
| 172 | Univariate | /ˌjuːnɪˈvɛəriət/ | Đơn biến |
| 173 | Multivariate | /ˌmʌltɪˈvɛəriət/ | Đa biến |
| 174 | Huynh-Feldt correction | /wɪn fɛlt kəˈrɛkʃən/ | Hiệu chỉnh Huynh-Feldt |
| 175 | Departure from Sphericity | /dɪˈpɑːtʃər frəm sfɪˈrɪsəti/ | Sự sai lệch khỏi tính cầu |
| 176 | Row percentages | /roʊ pəˈsɛntɪdʒɪz/ | Tỷ lệ phần trăm theo hàng |
| 177 | Count data | /kaʊnt ˈdeɪtə/ | Dữ liệu đếm |
| 178 | Two-sided | /tuː ˈsaɪdɪd/ | (Kiểm định) hai phía |
| 179 | Chi-square components | /kaɪ skwɛər kəmˈpoʊnənts/ | Các thành phần chi-bình phương |
| 180 | Noncentrality parameter | /ˌnɒnsɛnˈtræləti pəˈræmɪtər/ | Tham số phi trung tâm |
| 181 | Numerator df | /ˈnjuːməreɪtər diː ɛf/ | Bậc tự do của tử số |
| 182 | Denominator df | /dɪˈnɒmɪneɪtər diː ɛf/ | Bậc tự do của mẫu số |
| 183 | Actual power | /ˈæktʃuəl ˈpaʊər/ | Công suất (độ mạnh) thực tế |
| 184 | Scholarly practices | /ˈskɒləli ˈpræktɪsɪz/ | Các thực hành học thuật |
| 185 | Journal | /ˈdʒɜːnl/ | Tạp chí (khoa học) |
| 186 | Affiliations | /əˌfɪliˈeɪʃənz/ | Các đơn vị công tác |
| 187 | Reputation | /ˌrɛpjuˈteɪʃən/ | Danh tiếng |
| 188 | Constraints | /kənˈstreɪnts/ | Các ràng buộc, hạn chế |
| 189 | Guidelines | /ˈɡaɪdlaɪnz/ | Các hướng dẫn |
| 190 | Elementary designs | /ˌɛlɪˈmɛntəri dɪˈzaɪnz/ | Các thiết kế cơ bản |
| 191 | Communication | /kəˌmjuːnɪˈkeɪʃən/ | Sự giao tiếp, trao đổi |
| 192 | Ramifications | /ˌræmɪfɪˈkeɪʃənz/ | Các hệ quả |
| 193 | Violating assumptions | /ˈvaɪəleɪtɪŋ əˈsʌmpʃənz/ | Vi phạm các giả định |
| 194 | Interval data | /ˈɪntəvəl ˈdeɪtə/ | Dữ liệu khoảng |
| 195 | Ordinal data | /ˈɔːdɪnl ˈdeɪtə/ | Dữ liệu thứ bậc |
| 196 | Nominal data | /ˈnɒmɪnl ˈdeɪtə/ | Dữ liệu danh nghĩa |
| 197 | Experimental design | /ɪkˌspɛrɪˈmɛntl dɪˈzaɪn/ | Thiết kế thực nghiệm |
| 198 | Composite measure | /ˈkɒmpəzɪt ˈmɛʒər/ | Thước đo tổng hợp |
| 199 | Follow-up analyses | /ˈfɒloʊ ʌp əˈnæləsiːz/ | Các phân tích theo dõi |
| 200 | Pairwise differences | /ˈpɛəwaɪz ˈdɪfrənsɪz/ | Các chênh lệch cặp |
