Thống kê Sinh học Cơ bản và Lâm sàng, Ấn bản thứ 5 – Basic & Clinical Biostatistics, 5e
Tác giả: Susan White – Nhà xuất bản McGraw-Hill Medical – Biên dịch: Ths.Bs. Lê Đình Sáng

Chương 8: Các Câu Hỏi Nghiên Cứu Về Mối Quan Hệ Giữa Các Biến Số

Research Questions About Relationships Among Variables

CÁC KHÁI NIỆM CHÍNH

Tương quan và hồi quy là các phương pháp thống kê dùng để kiểm tra mối quan hệ tuyến tính giữa hai biến số định lượng được đo lường trên cùng một đối tượng. Tương quan mô tả một mối quan hệ, còn hồi quy vừa mô tả mối quan hệ vừa dự đoán một kết quả.
Hệ số tương quan có giá trị từ -1 đến +1, cả hai giá trị này đều chỉ ra một mối quan hệ hoàn hảo giữa hai biến số. Hệ số tương quan bằng 0 cho thấy không có mối quan hệ.
Biểu đồ phân tán cung cấp một cái nhìn trực quan về mối quan hệ giữa hai biến số định lượng và được khuyến nghị sử dụng để kiểm tra mối quan hệ tuyến tính và các giá trị ngoại lai.
Hệ số xác định, hay $r^{2}$ , đơn giản là bình phương của hệ số tương quan; đây là thống kê được ưu tiên sử dụng để mô tả độ mạnh của mối quan hệ giữa hai biến số định lượng.
Kiểm định t có thể được sử dụng để kiểm định giả thuyết rằng hệ số tương quan trong quần thể bằng không.
Phép biến đổi z của Fisher được sử dụng để tạo khoảng tin cậy cho hệ số tương quan hoặc để kiểm định bất kỳ giả thuyết nào về giá trị của hệ số tương quan.
Phép biến đổi z của Fisher cũng có thể được sử dụng để tạo khoảng tin cậy cho sự khác biệt giữa các hệ số tương quan trong hai nhóm độc lập.
Có thể kiểm định xem hệ số tương quan giữa một biến và biến thứ hai có giống với hệ số tương quan giữa biến thứ ba và biến thứ hai hay không.
Khi một hoặc cả hai biến trong phân tích tương quan bị lệch, nên sử dụng hệ số tương quan phi tham số rho của Spearman.
Hồi quy tuyến tính được gọi là tuyến tính vì nó chỉ đo lường các mối quan hệ theo đường thẳng.
Phương pháp bình phương tối thiểu là phương pháp được sử dụng trong hầu hết các ví dụ về hồi quy trong y học. Với một biến độc lập và một biến phụ thuộc, phương trình hồi quy có thể được biểu diễn dưới dạng một đường thẳng.
Sai số chuẩn của ước lượng là một thống kê có thể được sử dụng để kiểm định giả thuyết hoặc tạo khoảng tin cậy cho cả hệ số chặn và hệ số hồi quy (độ dốc).
Một ứng dụng quan trọng của hồi quy là khả năng dự đoán kết quả trong một nhóm đối tượng trong tương lai.
Khi dự đoán kết quả, giới hạn tin cậy được gọi là dải tin cậy quanh đường hồi quy. Các dự đoán chính xác nhất là cho các kết quả gần với giá trị trung bình của biến độc lập X, và chúng trở nên kém chính xác hơn khi kết quả càng xa giá trị trung bình.
Có thể kiểm định xem đường hồi quy có giống nhau (tức là có cùng độ dốc và hệ số chặn) trong hai nhóm khác nhau hay không.
Phần dư là sự khác biệt giữa kết quả thực tế và kết quả dự đoán; việc xem xét phân phối của phần dư giúp các nhà thống kê quyết định xem mô hình hồi quy tuyến tính có phải là phương pháp tốt nhất để phân tích dữ liệu hay không.
Hồi quy về giá trị trung bình có thể dẫn đến việc một phương pháp điều trị hoặc thủ thuật có vẻ như có giá trị trong khi thực tế không có tác dụng gì; việc có một nhóm chứng giúp phòng tránh vấn đề này.
Không nên sử dụng tương quan và hồi quy trừ khi các quan sát là độc lập; không phù hợp khi bao gồm nhiều phép đo trên cùng một đối tượng.
Việc gộp hai quần thể cũng có thể làm cho hệ số tương quan và hệ số hồi quy lớn hơn giá trị thực của chúng.
Việc sử dụng tương quan hay hồi quy nên được quyết định bởi mục đích của nghiên cứu—cho dù đó là để thiết lập một mối quan hệ hay để dự đoán một kết quả.
Mô hình hồi quy có thể được mở rộng để bao gồm hai hoặc nhiều biến độc lập; mô hình này được gọi là hồi quy đa biến.
Việc xác định cỡ mẫu cần thiết cho tương quan và hồi quy không khó khi sử dụng một trong các chương trình thống kê phân tích công suất.

Các vấn đề tình huống

Vấn đề tình huống 1

Neidert và cộng sự (2016) đã nghiên cứu mối quan hệ giữa các chỉ số thành phần cơ thể: hoạt độ DPP-IV huyết tương, mỡ vùng hông đùi (gynoid fat), chỉ số khối cơ thể (BMI) và khối lượng nạc. Họ đã tuyển 111 đối tượng từ Đại học Auburn (40 nam và 71 nữ) và thu thập các biến số về thành phần cơ thể cho nghiên cứu.

Vấn đề tình huống 2

Pereira và cộng sự (2015) đã thu thập dữ liệu từ 145 bệnh nhân tại một đơn vị hồi sức tích cực (ICU) hỗn hợp dành cho người lớn để nghiên cứu độ chính xác của các thiết bị dùng để đo đường huyết tại giường. Họ đã kiểm tra các thiết bị: Precision PCx, Accu-chek Advantage II (máu động mạch), Accu-check Advantage II (lấy máu đầu ngón tay) và Accu-check Advantage II (máu tĩnh mạch). Họ đã sử dụng các phương pháp hồi quy để đánh giá độ chính xác của từng thiết bị so với xét nghiệm máu động mạch tiêu chuẩn vàng từ phòng xét nghiệm trung tâm.

TỔNG QUAN VỀ TƯƠNG QUAN & HỒI QUY

Trong Chương 3, chúng ta đã giới thiệu các phương pháp để mô tả sự liên hợp hoặc mối quan hệ giữa hai biến số. Trong chương này, chúng ta sẽ xem xét lại các khái niệm này và mở rộng ý tưởng sang việc dự đoán giá trị của một đặc tính từ một đặc tính khác. Chúng ta cũng sẽ trình bày các quy trình thống kê được sử dụng để kiểm định xem một mối quan hệ giữa hai đặc tính có ý nghĩa thống kê hay không. Hai phân phối xác suất đã được giới thiệu trước đây, phân phối t và phân phối chi-bình phương, có thể được sử dụng cho các kiểm định thống kê trong tương quan và hồi quy. Do đó, bạn sẽ vui mừng khi biết rằng phần lớn nội dung trong chương này sẽ quen thuộc với bạn.

Khi mục tiêu chỉ đơn thuần là thiết lập một mối quan hệ (hoặc liên hợp) giữa hai phép đo, như trong các nghiên cứu này, hệ số tương quan (đã được giới thiệu trong Chương 3) là thống kê thường được sử dụng nhất. Hãy nhớ lại rằng tương quan là một thước đo về mối quan hệ tuyến tính giữa hai biến số được đo trên thang đo định lượng.

Ngoài việc thiết lập một mối quan hệ, các nhà nghiên cứu đôi khi muốn dự đoán một biến kết quả, phụ thuộc, hoặc đáp ứng từ một biến độc lập, hoặc giải thích. Thông thường, đặc tính giải thích là đặc tính xảy ra trước hoặc dễ đo lường hơn hoặc ít tốn kém hơn. Phương pháp thống kê hồi quy tuyến tính được sử dụng; kỹ thuật này bao gồm việc xác định một phương trình để dự đoán giá trị của kết quả từ các giá trị của biến giải thích. Một trong những khác biệt chính giữa tương quan và hồi quy là mục đích của phân tích—liệu nó chỉ đơn thuần là để mô tả một mối quan hệ hay để dự đoán một giá trị. Cũng có một số điểm tương đồng quan trọng, bao gồm mối quan hệ trực tiếp giữa hệ số tương quan và hệ số hồi quy. Nhiều giả định giống nhau được yêu cầu cho cả tương quan và hồi quy, và cả hai đều đo lường mức độ của một mối quan hệ tuyến tính giữa hai đặc tính.

TƯƠNG QUAN

Hình 8-1 minh họa một số biểu đồ phân tán giả định của dữ liệu để chứng minh mối quan hệ giữa độ lớn của hệ số tương quan và hình dạng của biểu đồ phân tán. Khi hệ số tương quan gần bằng không, như trong Hình 8-1E, dạng phân bố của các điểm được vẽ có phần tròn. Khi mức độ quan hệ nhỏ, dạng phân bố giống hình bầu dục hơn, như trong Hình 8-1D và 8-1B. Khi giá trị của hệ số tương quan tiến gần đến +1 hoặc -1, như trong Hình 8-1C, biểu đồ có hình dạng dài và hẹp; tại +1 và -1, các quan sát nằm chính xác trên một đường thẳng, như trường hợp $r = + 1.0$ trong Hình 8-1A.

Biểu đồ phân tán trong Hình 8-1F minh họa một tình huống trong đó tồn tại một mối quan hệ mạnh nhưng phi tuyến. Ví dụ, với nhiệt độ dưới $1 0^{\circ} C$ đến $1 5^{\circ} C$ , một sợi thần kinh cảm nhận lạnh phát ra ít xung động; khi nhiệt độ tăng, số lượng xung động mỗi giây cũng tăng cho đến khi nhiệt độ đạt khoảng $2 5^{\circ} C$ . Khi nhiệt độ tăng quá $2 5^{\circ} C$ , số lượng xung động mỗi giây lại giảm đi, cho đến khi chúng ngừng hẳn ở $4 0^{\circ} C$ đến $4 5^{\circ} C$ . Tuy nhiên, hệ số tương quan chỉ đo lường mối quan hệ tuyến tính, và nó có giá trị gần bằng không trong tình huống này.

Một trong những lý do để tạo biểu đồ phân tán của dữ liệu như một phần của phân tích ban đầu là để xác định các mối quan hệ phi tuyến khi chúng xảy ra. Nếu không, nếu các nhà nghiên cứu tính toán hệ số tương quan mà không kiểm tra dữ liệu, họ có thể bỏ lỡ một mối quan hệ mạnh nhưng phi tuyến, chẳng hạn như mối quan hệ giữa nhiệt độ và số lượng xung động của sợi thần kinh cảm nhận lạnh.

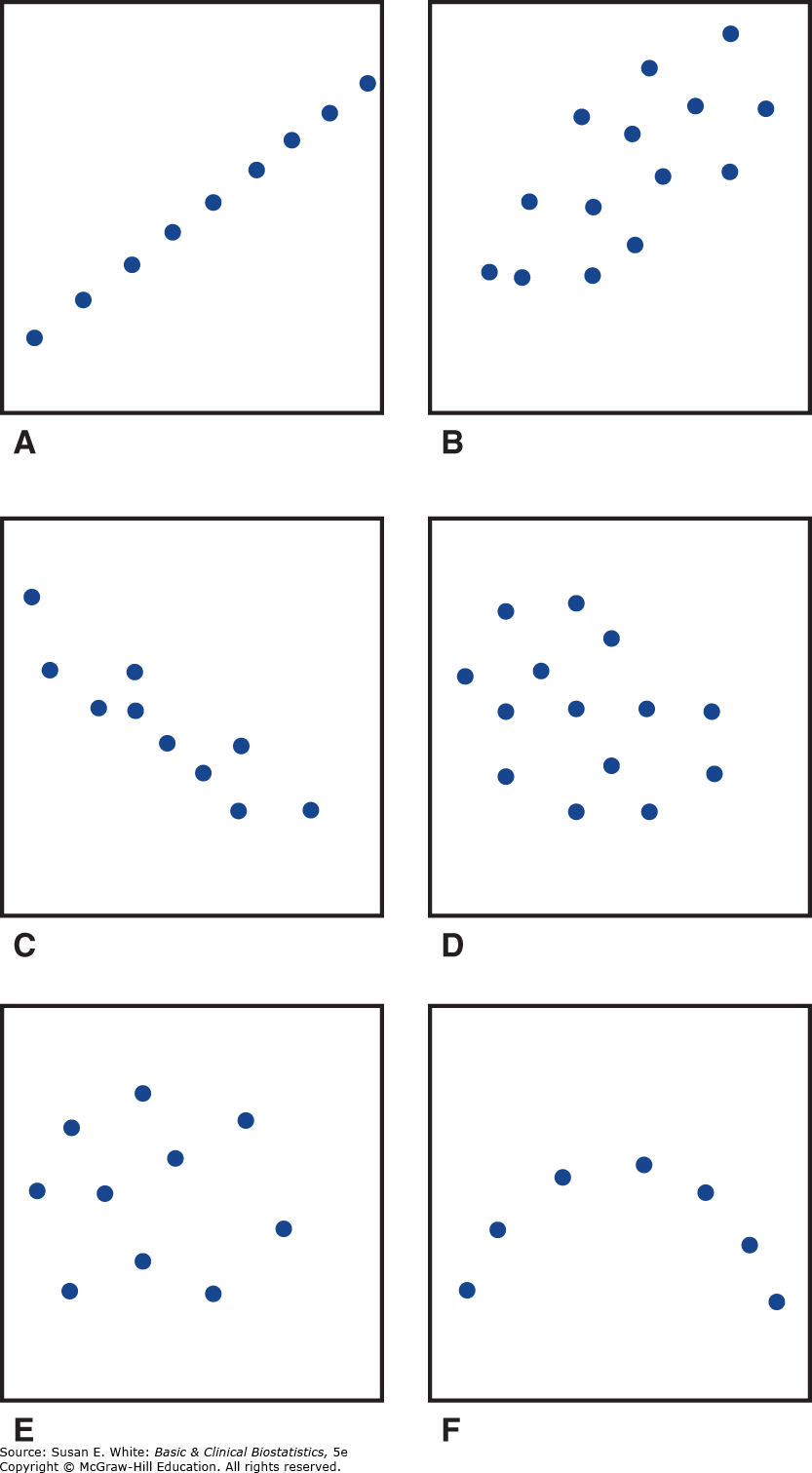
Hình 8-1. Biểu đồ phân tán và các hệ số tương quan. A: $r = + 1.0$ ; B: $r = 0.7$ ; C: $r = - 0.9$ ; D: $r = - 0.4$ ; E: $r = 0.0$ ; F: $r = 0.0$ .

Tính toán Hệ số Tương quan

Chúng ta sử dụng nghiên cứu của Neidert và cộng sự (2016) để mở rộng hiểu biết của mình về tương quan. Chúng tôi giả định rằng bất kỳ ai quan tâm đến việc tính toán thực tế hệ số tương quan sẽ sử dụng một chương trình máy tính, như chúng tôi làm trong chương này. Nếu bạn quan tâm đến một minh họa chi tiết về các phép tính, hãy tham khảo Chương 3, trong phần có tựa đề “Mô tả Mối quan hệ giữa Hai Đặc tính,” và nghiên cứu của Bos-Touwen và cộng sự (2015).

Hãy nhớ lại rằng công thức cho hệ số tương quan Pearson product-moment, ký hiệu là r, là:

$r = \frac{\sum(X - \overline{X})(Y - \overline{Y})}{\sqrt{\sum(X - \overline{X})^2 \sum(Y - \overline{Y})^2}}$

trong đó X là biến độc lập và Y là biến kết quả.

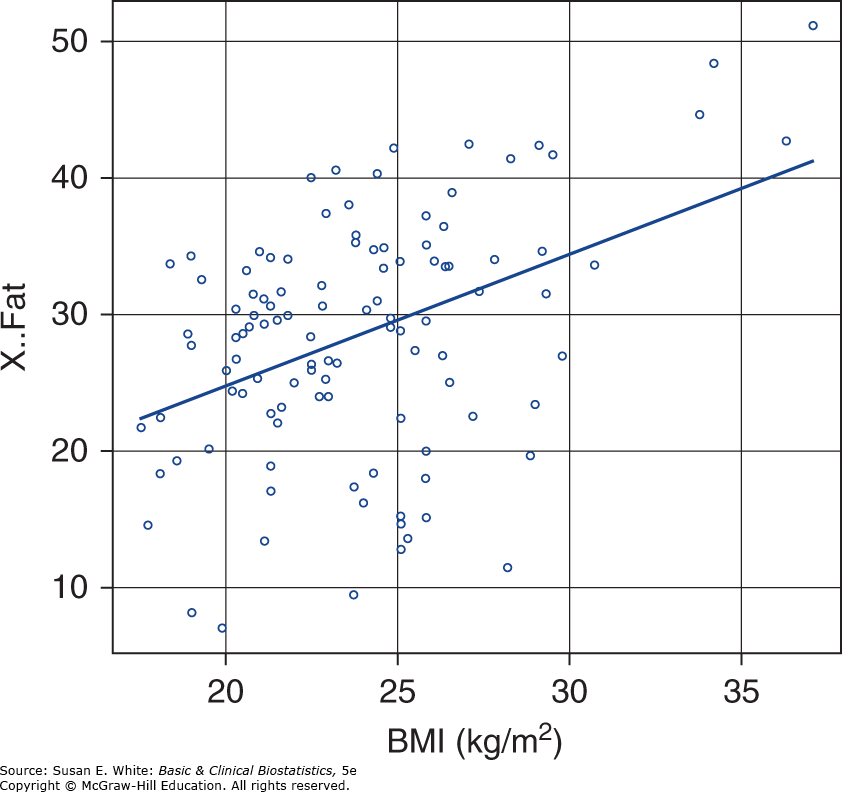
Một bước đầu tiên rất được khuyến nghị khi xem xét mối quan hệ giữa hai đặc tính định lượng là kiểm tra mối quan hệ đó một cách trực quan. Hình 8-2 là một biểu đồ phân tán của dữ liệu, với chỉ số khối cơ thể (BMI) trên trục X và tỷ lệ mỡ cơ thể (% Fat) trên trục Y. Từ Hình 8-2, chúng ta thấy rằng có một mối quan hệ dương giữa hai đặc tính này: các giá trị BMI nhỏ đi kèm với các giá trị tỷ lệ mỡ cơ thể nhỏ. Câu hỏi quan tâm là liệu mối quan hệ quan sát được có ý nghĩa thống kê hay không.

Mức độ của mối quan hệ có thể được tìm thấy bằng cách tính toán hệ số tương quan. Sử dụng một chương trình thống kê, hệ số tương quan giữa BMI và tỷ lệ mỡ cơ thể là 0.42, cho thấy một mối quan hệ mạnh mẽ giữa hai chỉ số này. Hãy sử dụng R để xác nhận các tính toán của chúng tôi. Ngoài ra, xem Chương 3, trong phần có tựa đề “Mô tả Mối quan hệ giữa Hai Đặc tính,” để xem lại các thuộc tính của hệ số tương quan.

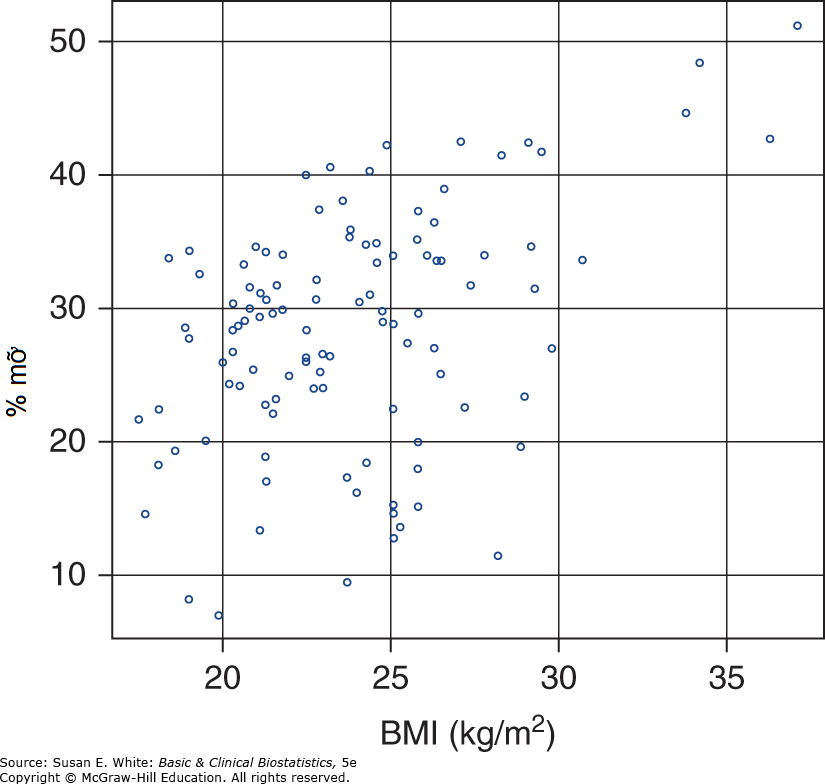
Hình 8-2. Biểu đồ phân tán của chỉ số khối cơ thể và tỷ lệ mỡ cơ thể. (Chuyển thể với sự cho phép từ Neidert LE, Wainright KS, Zheng C, và cộng sự: Plasma dipeptidyl peptidase IV activity and measures of body composition in apparently healthy people, Heliyon. 2016 Apr 18;2(4):e00097.)

Diễn giải Độ lớn của r

Độ lớn của hệ số tương quan cần thiết để có ý nghĩa thống kê liên quan đến cỡ mẫu. Với một mẫu rất lớn, chẳng hạn như 2.000 đối tượng, ngay cả các hệ số tương quan nhỏ, như 0.06, cũng có ý nghĩa thống kê. Một cách tốt hơn để diễn giải độ lớn của hệ số tương quan là xem xét nó cho chúng ta biết điều gì về độ mạnh của mối quan hệ.

Hệ số Xác định: Hệ số tương quan có thể được bình phương để tạo thành một thống kê gọi là hệ số xác định. Đối với các đối tượng trong nghiên cứu của Neidert và cộng sự (2016), hệ số xác định là $(0.42)^{2}$ , hay 0.18. Điều này có nghĩa là 18% sự biến thiên trong các giá trị của một trong các chỉ số, chẳng hạn như tỷ lệ mỡ cơ thể, có thể được giải thích bằng việc biết BMI. Khái niệm này được minh họa bằng các biểu đồ Venn trong Hình 8-3. Đối với biểu đồ bên trái, $r^{2} = 0.25$ ; do đó 25% sự biến thiên trong A được giải thích bằng việc biết B (hoặc ngược lại). Biểu đồ ở giữa minh họa $r^{2} = 0.50$ và biểu đồ bên phải đại diện cho $r^{2} = 0.80$ .

Hệ số xác định cho chúng ta biết mối quan hệ thực sự mạnh đến mức nào. Trong y văn, các giới hạn tin cậy hoặc kết quả của một kiểm định thống kê về ý nghĩa của hệ số tương quan cũng thường được trình bày.

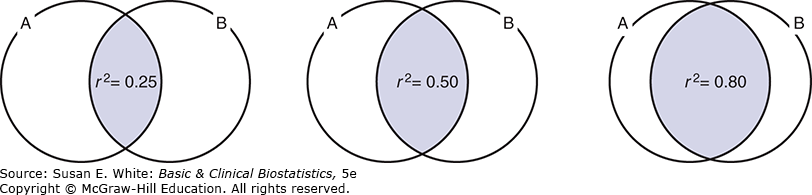
Hình 8-3. Minh họa về $r^{2}$ , tỷ lệ phương sai được giải thích.

Kiểm định t cho Tương quan: Ký hiệu cho hệ số tương quan trong quần thể (tham số quần thể) là $ρ$ (chữ rho Hy Lạp viết thường). Trong một mẫu ngẫu nhiên, $ρ$ được ước tính bằng r. Nếu một số mẫu ngẫu nhiên có cùng kích thước được chọn từ một quần thể nhất định và hệ số tương quan được tính cho mỗi mẫu, chúng ta mong đợi $r$ sẽ thay đổi từ mẫu này sang mẫu khác nhưng tuân theo một loại phân phối nào đó quanh giá trị quần thể $ρ$ . Thật không may, phân phối lấy mẫu của hệ số tương quan không hoạt động tốt như phân phối lấy mẫu của giá trị trung bình, vốn có phân phối chuẩn cho các mẫu lớn.

Một phần của vấn đề là hiệu ứng trần khi hệ số tương quan tiến gần đến -1 hoặc +1. Nếu giá trị của tham số quần thể là, chẳng hạn, 0.8, các giá trị mẫu chỉ có thể vượt quá 0.8 đến 1.0, nhưng chúng có thể nhỏ hơn 0.8 xuống đến -1.0. Giá trị tối đa 1.0 hoạt động như một cái trần, giữ cho các giá trị mẫu không biến thiên nhiều hơn ở phía trên 0.8 so với phía dưới nó, và kết quả là một phân phối lệch. Tuy nhiên, khi tham số quần thể được giả thuyết là bằng không, hiệu ứng trần tại +1 và -1 là bằng nhau, và các giá trị mẫu được phân phối xấp xỉ theo phân phối t, có thể được sử dụng để kiểm định giả thuyết rằng giá trị thực của tham số quần thể $ρ$ bằng không. Biểu thức toán học sau đây liên quan đến hệ số tương quan, thường được gọi là tỷ số t, đã được chứng minh là có phân phối t với $n - 2$ bậc tự do:

$t = \frac{r\sqrt{n-2}}{\sqrt{1-r^2}}$

Hãy sử dụng tỷ số này để kiểm định xem giá trị quan sát được $r = 0.42$ với 109 quan sát có đủ bằng chứng để kết luận rằng giá trị thực của hệ số tương quan trong quần thể $ρ$ khác không hay không.

Bước 1: $H_{0}$ : Không có mối quan hệ nào tồn tại giữa BMI và tỷ lệ mỡ cơ thể; hay, hệ số tương quan thực sự bằng không: $ρ = 0$ . $H_{1}$ : Có một mối quan hệ tồn tại giữa BMI và tỷ lệ mỡ cơ thể; hay, hệ số tương quan thực sự khác không: $ρ \neq = 0$ .
Bước 2: Vì giả thuyết không là một kiểm định về việc $ρ$ có bằng không hay không, tỷ số t có thể được sử dụng khi các giả định cho tương quan (xem phần “Các giả định trong Tương quan”) được đáp ứng.
Bước 3: Hãy sử dụng $α = 0.01$ cho ví dụ này.
Bước 4: Bậc tự do là $n - 2 = 111 - 2 = 109$ . Giá trị của phân phối t với 109 bậc tự do chia khu vực thành 99% trung tâm và 1% ở hai đuôi trên và dưới là khoảng 2.617 (sử dụng giá trị cho 120 df trong Bảng A-3). Do đó, chúng ta bác bỏ giả thuyết không về tương quan bằng không nếu (giá trị tuyệt đối của) giá trị t quan sát được lớn hơn 2.617.
Bước 5: Phép tính là: $t = 1 - 0.42 ^{2} 0.42 109 = 4.79$
Bước 6: Giá trị quan sát được của tỷ số t với 109 bậc tự do là 4.79, lớn hơn giá trị tới hạn 2.617. Do đó, giả thuyết không về tương quan bằng không bị bác bỏ, và chúng ta kết luận rằng mối quan hệ giữa BMI và tỷ lệ mỡ cơ thể đủ lớn để kết luận rằng hai biến này có liên quan với nhau.

Phép biến đổi z của Fisher để Kiểm định Tương quan: Các nhà nghiên cứu thường muốn biết liệu $ρ = 0$ và kiểm định này có thể dễ dàng thực hiện bằng các chương trình máy tính. Tuy nhiên, đôi khi, mối quan tâm lại nằm ở việc liệu hệ số tương quan có bằng một giá trị cụ thể khác không hay không. Ví dụ, hãy xem xét một xét nghiệm chẩn đoán cho kết quả định lượng chính xác nhưng lại xâm lấn và có phần rủi ro cho bệnh nhân. Nếu ai đó phát triển một quy trình xét nghiệm thay thế, điều quan trọng là phải chứng minh rằng quy trình mới cũng chính xác như xét nghiệm đang được sử dụng. Cách tiếp cận là chọn một mẫu bệnh nhân và thực hiện cả xét nghiệm hiện tại và quy trình mới trên mỗi bệnh nhân, sau đó tính toán hệ số tương quan giữa hai quy trình xét nghiệm.

Có thể thực hiện kiểm định giả thuyết để chứng minh rằng hệ số tương quan lớn hơn một giá trị cho trước, hoặc có thể tính toán một khoảng tin cậy quanh hệ số tương quan quan sát được. Trong cả hai trường hợp, chúng ta sử dụng một quy trình gọi là phép biến đổi z của Fisher để kiểm định bất kỳ giả thuyết không nào về hệ số tương quan cũng như để tạo các khoảng tin cậy.

Để sử dụng kiểm định chính xác của Fisher, trước tiên chúng ta biến đổi hệ số tương quan và sau đó sử dụng phân phối chuẩn (z). Chúng ta cần biến đổi hệ số tương quan vì, như đã đề cập trước đó, phân phối của các giá trị mẫu của hệ số tương quan bị lệch khi $ρ \neq = 0$ . Mặc dù phương pháp này hơi phức tạp, nó thực sự linh hoạt hơn kiểm định t, vì nó cho phép chúng ta kiểm định bất kỳ giả thuyết không nào, không chỉ đơn giản là hệ số tương quan bằng không. Phép biến đổi z của Fisher được đề xuất bởi cùng một nhà thống kê (Ronald Fisher) người đã phát triển kiểm định chính xác của Fisher cho các bảng dự phòng $2 \times 2$ (được thảo luận trong Chương 6). Phép biến đổi z của Fisher là:

$z(r) = \frac{1}{2} \ln(\frac{1+r}{1-r})$

trong đó $ln$ là logarit tự nhiên. Bảng A-6 cung cấp phép biến đổi z cho các giá trị khác nhau của r, vì vậy chúng ta không thực sự cần sử dụng công thức. Với các mẫu có kích thước vừa phải, phép biến đổi này tuân theo phân phối chuẩn, và biểu thức sau cho kiểm định z có thể được sử dụng:

$z = \frac{z(r) - z(\rho)}{\sqrt{1/(n-3)}}$

Để minh họa phép biến đổi z của Fisher để kiểm định ý nghĩa của $ρ$ , chúng ta đánh giá mối quan hệ giữa BMI và tỷ lệ mỡ cơ thể (Neidert và cộng sự, 2016). Hệ số tương quan quan sát được giữa hai chỉ số này là 0.42. Neidert và cộng sự (2016) có thể đã kỳ vọng một hệ số tương quan đáng kể giữa hai chỉ số này; giả sử họ muốn biết liệu hệ số tương quan có lớn hơn 0.25 một cách có ý nghĩa thống kê hay không. Một kiểm định một phía của giả thuyết không rằng $ρ \leq 0.25$ , mà họ hy vọng sẽ bác bỏ, có thể được thực hiện như sau.

Bước 1: $H_{0}$ : Mối quan hệ giữa BMI và tỷ lệ mỡ cơ thể là $\leq 0.25$ ; hay, hệ số tương quan thực sự $ρ \leq 0.25$ . $H_{1}$ : Mối quan hệ giữa BMI và tỷ lệ mỡ cơ thể là $> 0.25$ ; hay, hệ số tương quan thực sự $ρ > 0.25$ .
Bước 2: Phép biến đổi z của Fisher có thể được sử dụng với hệ số tương quan để kiểm định bất kỳ giả thuyết nào.
Bước 3: Hãy sử dụng lại $α = 0.01$ cho ví dụ này.
Bước 4: Giả thuyết đối là một kiểm định một phía. Giá trị của phân phối z chia khu vực thành 99% dưới và 1% trên là khoảng 2.326 (từ Bảng A-2). Do đó, chúng ta bác bỏ giả thuyết không rằng hệ số tương quan là $\leq 0.25$ nếu giá trị z quan sát được > 2.326.
Bước 5: Bước đầu tiên là tìm các giá trị biến đổi cho $r = 0.42$ và $ρ = 0.25$ từ Bảng A-6; các giá trị này lần lượt là 0.448 và 0.255. Sau đó, phép tính cho kiểm định z là: $z = 1/ ( 111 - 3 ) z ( 0.42 ) - z ( 0.25 ) = 0.096 0.448 - 0.255 = 2.01$
Bước 6: Giá trị quan sát được của thống kê z, 2.01, không vượt quá 2.326. Giả thuyết không rằng hệ số tương quan là 0.25 hoặc nhỏ hơn không bị bác bỏ.

Khoảng Tin cậy cho Hệ số Tương quan: Một ưu điểm lớn của phép biến đổi z của Fisher là có thể tạo ra các khoảng tin cậy. Giá trị biến đổi của hệ số tương quan được sử dụng để tính toán các giới hạn tin cậy theo cách thông thường, và sau đó chúng được biến đổi ngược lại thành các giá trị tương ứng với hệ số tương quan.

Để minh họa, chúng ta tính khoảng tin cậy 95% cho hệ số tương quan 0.42 trong nghiên cứu của Neidert và cộng sự (2016). Chúng ta sử dụng phép biến đổi z của Fisher cho $0.42 = 0.448$ và phân phối z trong Bảng A-2 để tìm giá trị tới hạn cho 95%. Khoảng tin cậy là:

Giá trị biến đổi z của $r \pm$ hệ số tin cậy $\times$ sai số chuẩn Giá trị biến đổi z của $z(r) \pm 1.96 \times \sqrt{1/(n-3)}$

Biến đổi ngược các giới hạn 0.260 và 0.636 về lại hệ số tương quan bằng cách sử dụng Bảng A-6 ngược lại cho ra xấp xỉ $r = 0.25$ và $r = 0.56$ (sử dụng các giá trị thận trọng). Do đó, chúng ta tin tưởng 95% rằng giá trị thực của hệ số tương quan trong quần thể nằm trong khoảng này. R có một hàm tính toán khoảng tin cậy cho hệ số tương quan. Hàm này cho kết quả trong khoảng từ 0.26 đến 0.56, rất gần với giá trị xấp xỉ được tính bằng Bảng A-6.

Các giả định trong Tương quan

Các giả định cần thiết để đưa ra kết luận hợp lệ về hệ số tương quan là mẫu được chọn ngẫu nhiên và hai biến, X và Y, cùng biến thiên trong một phân phối phối hợp có dạng chuẩn, được gọi là phân phối chuẩn hai biến. Tuy nhiên, chỉ vì mỗi biến có phân phối chuẩn khi được kiểm tra riêng lẻ không đảm bảo rằng, khi phối hợp, chúng có phân phối chuẩn hai biến. Có một số hướng dẫn: nếu một trong hai biến không có phân phối chuẩn, hệ số tương quan Pearson product-moment không phải là phương pháp phù hợp nhất. Thay vào đó, một hoặc cả hai biến có thể được biến đổi để chúng tuân theo phân phối chuẩn gần hơn, như đã thảo luận trong Chương 5, hoặc có thể tính toán hệ số tương quan hạng Spearman. Chủ đề này được thảo luận trong phần “Các Thước đo Tương quan Khác.”

SO SÁNH HAI HỆ SỐ TƯƠNG QUAN

Đôi khi, các nhà nghiên cứu muốn biết liệu có sự khác biệt giữa hai hệ số tương quan hay không. Dưới đây là hai trường hợp cụ thể: (1) so sánh các hệ số tương quan giữa cùng hai biến đã được đo lường trong hai nhóm đối tượng độc lập và (2) so sánh hai hệ số tương quan có liên quan đến một biến chung trong cùng một nhóm cá nhân. Những tình huống này không quá phổ biến và không phải lúc nào cũng có sẵn trong các chương trình thống kê.

So sánh Tương quan trong Hai Nhóm Độc lập

Phép biến đổi z của Fisher có thể được sử dụng để kiểm định giả thuyết hoặc tạo khoảng tin cậy về sự khác biệt giữa các hệ số tương quan của cùng hai biến trong hai nhóm độc lập. Kết quả của các kiểm định như vậy còn được gọi là tương quan độc lập. Ví dụ, quay lại dữ liệu từ nghiên cứu của Neidert và cộng sự (2016), chúng ta có thể so sánh hệ số tương quan giữa BMI và tỷ lệ mỡ cơ thể theo giới tính, xem Hình 8-4.

Hệ số tương quan giữa BMI và tỷ lệ mỡ cơ thể là 0.737 cho 71 đối tượng nữ và 0.508 cho 40 đối tượng nam. Trong tình huống này, giá trị cho nhóm thứ hai thay thế $z (ρ)$ trong tử số của kiểm định z được trình bày ở phần trước, và $1/ (n - 3)$ được tìm cho mỗi nhóm và cộng lại trước khi lấy căn bậc hai ở mẫu số. Thống kê kiểm định là:

Để minh họa, các giá trị z từ bảng biến đổi z của Fisher (A-6) cho 0.737 và 0.508 lần lượt là khoảng 0.951 và 0.563 (với làm tròn). Lưu ý rằng phép biến đổi z của Fisher là như nhau, bất kể hệ số tương quan là dương hay âm. Sử dụng các giá trị này, chúng ta có:

$z = \frac{0.951 - 0.563}{\sqrt{1/(71-3) + 1/(40-3)}} = \frac{0.388}{\sqrt{0.042}} = 1.89$

Giả sử chúng ta chọn mức ý nghĩa truyền thống là 0.05, giá trị của thống kê kiểm định, 1.89, nhỏ hơn giá trị tới hạn, 1.96, vì vậy chúng ta không bác bỏ giả thuyết không về các hệ số tương quan bằng nhau. Chúng ta quyết định rằng không đủ bằng chứng để kết luận rằng mối quan hệ giữa BMI và tỷ lệ mỡ cơ thể là khác nhau đối với nam và nữ. Lời giải thích khả dĩ cho việc thiếu ý nghĩa thống kê là gì? Có thể không có sự khác biệt trong mối quan hệ giữa hai biến này trong quần thể. Tuy nhiên, khi cỡ mẫu nhỏ, như trong nghiên cứu này, luôn nên ghi nhớ rằng nghiên cứu có thể có công suất thấp.

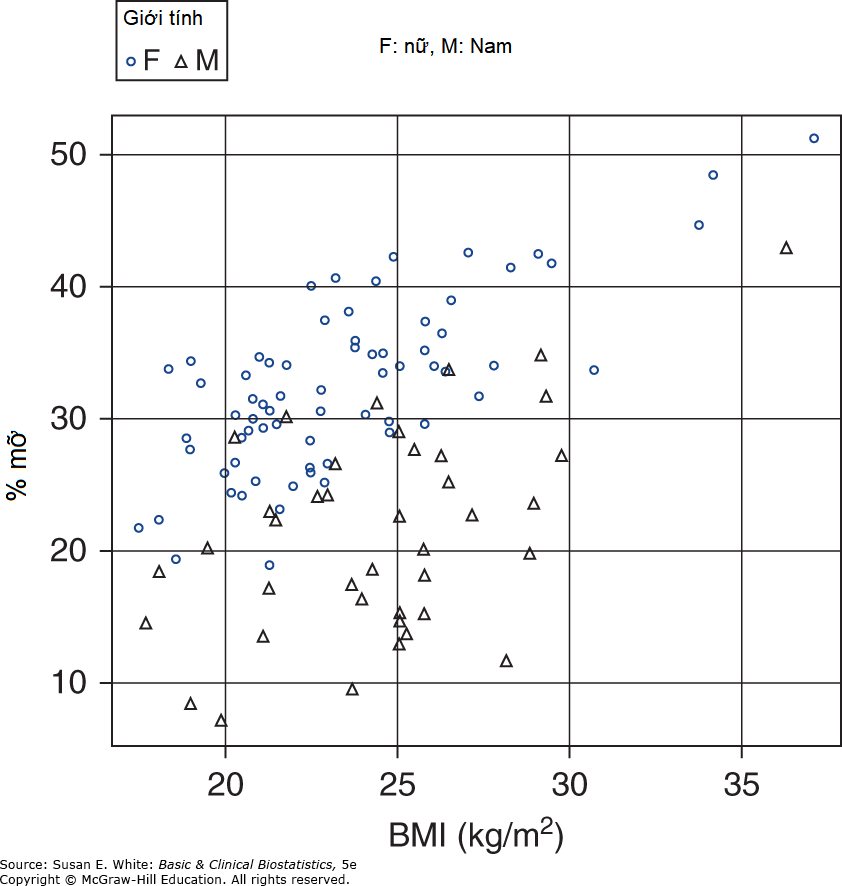
Hình 8-4. Biểu đồ phân tán của chỉ số khối cơ thể và tỷ lệ mỡ cơ thể theo giới tính. (Chuyển thể với sự cho phép từ Neidert LE, Wainright KS, Zheng C, và cộng sự: Plasma dipeptidyl peptidase IV activity and measures of body composition in apparently healthy people, Heliyon. 2016 Apr 18;2(4):e00097.)

So sánh các Tương quan có Biến chung trong cùng một Nhóm

Tình huống thứ hai xảy ra khi câu hỏi nghiên cứu liên quan đến các hệ số tương quan chứa cùng một biến (còn gọi là tương quan phụ thuộc). Ví dụ, một câu hỏi rất tự nhiên đối với Pereira và cộng sự (2015) là liệu một trong các thiết bị đo đường huyết tại giường có tương quan cao hơn với giá trị xét nghiệm động mạch trung tâm—được coi là tiêu chuẩn vàng—so với hai thiết bị còn lại hay không. Nếu vậy, đây sẽ là một sản phẩm mà họ có thể muốn giới thiệu cho bệnh nhân sử dụng tại nhà. Để minh họa, chúng ta so sánh đường huyết đo bằng Accu-chek động mạch với giá trị xét nghiệm động mạch trung tâm ( $r_{x y} = 0.57$ ) với đường huyết đo bằng Accu-chek đầu ngón tay với giá trị xét nghiệm động mạch trung tâm ( $r_{x z} = 0.87$ ).

Có một số công thức để kiểm định sự khác biệt giữa hai hệ số tương quan phụ thuộc. Chúng tôi trình bày công thức đơn giản nhất, được phát triển bởi Hotelling (1940) và được mô tả bởi Glass và Stanley (1970). Chúng tôi sẽ trình bày các phép tính cho ví dụ này nhưng, như mọi khi, đề nghị bạn sử dụng một chương trình máy tính. Công thức tuân theo phân phối t với $n - 3$ bậc tự do; nó trông khá đáng sợ và yêu cầu tính toán một số hệ số tương quan:

$t = (r_{xy} - r_{xz}) \sqrt{\frac{(n-3)(1+r_{yz})}{2(1 - r_{xy}^2 - r_{xz}^2 - r_{yz}^2 + 2r_{xy}r_{xz}r_{yz})}}$

Chúng ta ký hiệu giá trị xét nghiệm động mạch trung tâm là X, Accu-chek động mạch là Y, và Accu-chek đầu ngón tay là Z. Do đó, chúng ta muốn so sánh $r_{x y}$ với $r_{x z}$ . Cả hai hệ số tương quan đều liên quan đến X, hay giá trị xét nghiệm động mạch trung tâm, vì vậy các hệ số tương quan này là phụ thuộc. Để sử dụng công thức, chúng ta cũng cần tính hệ số tương quan giữa Accu-chek động mạch và Accu-chek đầu ngón tay, là $r_{yz} = 0.67$ .

Bảng 8-1 cho thấy các hệ số tương quan cần thiết cho công thức này. Các phép tính là:

Đến bây giờ bạn đã biết rằng sự khác biệt giữa hai hệ số tương quan này là có ý nghĩa thống kê vì giá trị t quan sát được là -3.22, và $∣ - 3.22∣ = 3.22$ lớn hơn giá trị tới hạn của t với 142 bậc tự do, là 1.97.

Bảng 8-1. Ma trận tương quan của các phép đo đường huyết cho 145 đối tượng.

	Xét nghiệm động mạch trung tâm (mg/dL)	Accu-chek động mạch (mg/dL)	Accu-chek đầu ngón tay (mg/dL)	Accu-chek catheter tĩnh mạch trung tâm (mg/dL)
Xét nghiệm động mạch trung tâm (mg/dL)	1.000
Accu-chek động mạch (mg/dL)	0.570	1.000
Accu-chek đầu ngón tay (mg/dL)	0.867	0.666	1.000
Accu-chek catheter tĩnh mạch trung tâm (mg/dL)	0.780	0.710	0.696	1.000
Dữ liệu từ Pereira AJ, Corrêa TD, de Almeida FP, và cộng sự: Inaccuracy of venous point-of-care glucose measurements in critically ill patients: a cross-sectional study, PLoS One. 2015 Jun 12;10(6):e0129568.

CÁC THƯỚC ĐO TƯƠNG QUAN KHÁC

Một số thước đo tương quan khác thường được tìm thấy trong y văn. Hệ số rho của Spearman, hay tương quan hạng được giới thiệu trong Chương 3, được sử dụng với dữ liệu thứ bậc hoặc trong các tình huống mà các biến số định lượng không có phân phối chuẩn. Khi một câu hỏi nghiên cứu liên quan đến một biến định lượng và một biến danh nghĩa, một loại tương quan gọi là tương quan điểm-nhị phân được sử dụng. Với dữ liệu danh nghĩa, tỷ số nguy cơ (risk ratio), hoặc kappa ( $κ$ ), đã được thảo luận trong Chương 5, có thể được sử dụng.

Hệ số rho của Spearman

Hãy nhớ lại rằng giá trị của hệ số tương quan bị ảnh hưởng đáng kể bởi các giá trị ngoại lai và do đó không cung cấp một mô tả tốt về mối quan hệ giữa hai biến khi phân phối của chúng bị lệch hoặc chứa các giá trị ngoại lai. Ví dụ, hãy xem xét các mối quan hệ giữa các thiết bị đo đường huyết khác nhau từ Vấn đề tình huống 2. Để minh họa, chúng ta sử dụng 25 đối tượng đầu tiên từ nghiên cứu này, được liệt kê trong Bảng 8-2.

Bảng 8-2. Dữ liệu về đường huyết của 25 đối tượng đầu tiên.

Đối tượng	Xét nghiệm động mạch trung tâm (mg/dL)	Accu-chek động mạch (mg/dL)	Accu-chek đầu ngón tay (mg/dL)	Accu-chek catheter tĩnh mạch trung tâm (mg/dL)
1	186	198	207	195
2	202	227	221	221
3	115	127	125	135
4	155	152	161	142
5	124	137	130	119
6	193	182	196	190
7	165	192	175	188
8	130	136	128	331
9	92	83	92	84
10	129	125	111	129
11	259	258	257	274
12	89	78	84	95
13	168	181	210	193
14	137	132	128	119
15	137	131	150	138
16	161	182	175	203
17	974	90	600	600
18	84	72	80	78
19	134	108	125	111
20	192	217	196	221
21	194	200	226	217
22	242	242	255	235
23	118	127	137	120
24	104	104	89	94
25	126	119	115	600
Dữ liệu từ Pereira AJ, Corrêa TD, de Almeida FP, và cộng sự: Inaccuracy of venous point-of-care glucose measurements in critically ill patients: a cross-sectional study, PLoS One. 2015 Jun 12;10(6):e0129568.

Rất khó để biết liệu các quan sát có phân phối chuẩn hay không mà không xem xét biểu đồ của dữ liệu. Một số chương trình thống kê có các quy trình để vẽ các giá trị so với phân phối chuẩn để giúp các nhà nghiên cứu quyết định xem có nên sử dụng một quy trình phi tham số hay không. Một biểu đồ xác suất chuẩn cho phép đo Accu-chek đầu ngón tay được đưa ra trong Hình 8-5. Hãy sử dụng R để tạo các biểu đồ tương tự cho các phép đo của các thiết bị khác.

Khi các quan sát được vẽ trên biểu đồ, như trong Hình 8-5, có vẻ như dữ liệu thực sự có phần bị lệch. Như chúng tôi đã chỉ ra trong Chương 3, một phương pháp đơn giản để giải quyết vấn đề các quan sát ngoại lai trong tương quan là xếp hạng dữ liệu và sau đó tính toán lại hệ số tương quan trên các hạng để có được hệ số tương quan phi tham số được gọi là rho của Spearman, hay tương quan hạng. Để minh họa quy trình này, chúng ta tiếp tục sử dụng dữ liệu của 25 đối tượng đầu tiên trong nghiên cứu về các thiết bị đo đường huyết (Vấn đề tình huống 2). Hãy tập trung vào mối tương quan giữa giá trị xét nghiệm động mạch trung tâm và thiết bị Accu-chek đầu ngón tay, mà chúng ta đã biết là 0.87 trong phần “So sánh các Tương quan có Biến chung trong cùng một Nhóm.”

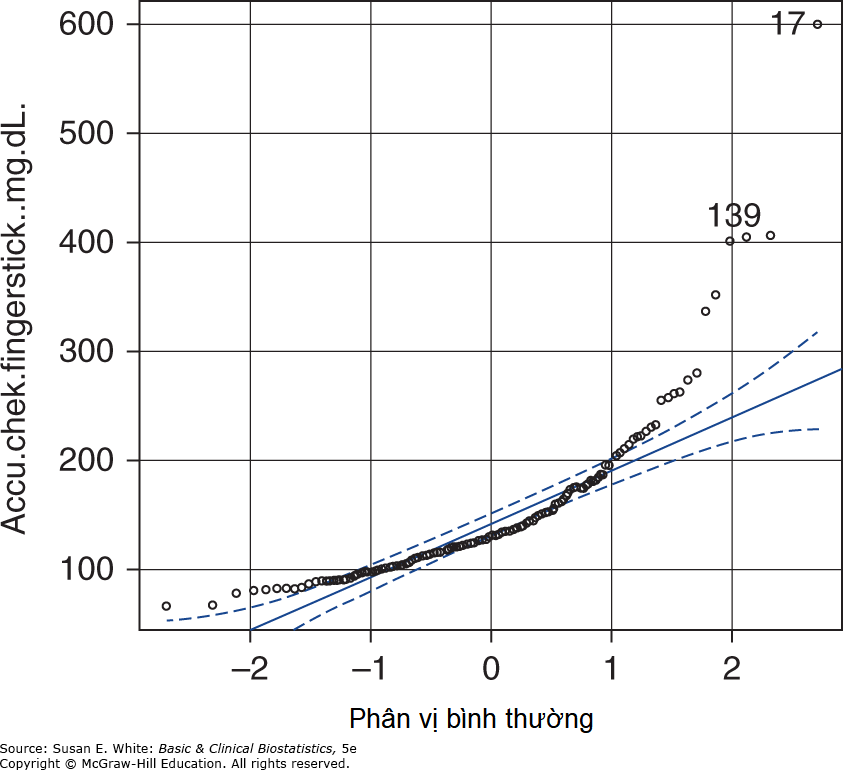
Hình 8-5. Biểu đồ xác suất chuẩn của đường huyết. (Dữ liệu từ Pereira AJ, Corrêa TD, de Almeida FP, và cộng sự: Inaccuracy of venous point-of-care glucose measurements in critically ill patients: a cross-sectional study, PLoS One. 2015 Jun 12;10(6):e0129568.)

Bảng 8-3 minh họa các hạng của các chỉ số đường huyết trên 25 đối tượng đầu tiên. Lưu ý rằng mỗi biến được xếp hạng riêng biệt; khi có các giá trị bằng nhau (ties), hạng trung bình của các giá trị bằng nhau được sử dụng.

Bảng 8-3. Thứ hạng của đường huyết cho 25 đối tượng đầu tiên.

Đối tượng	Hạng Xét nghiệm động mạch trung tâm (mg/dL)	Hạng Accu-chek động mạch (mg/dL)	Hạng Accu-chek đầu ngón tay (mg/dL)	Hạng Accu-chek catheter tĩnh mạch trung tâm (mg/dL)
1	8	6	7	10
2	4	3	5	6.5
3	21	16.5	18.5	16
4	12	11	12	14
5	19	12	15	19.5
6	6	8.5	8.5	12
7	10	7	10.5	13
8	16	13	16.5	3
9	23	23	22	24
10	17	18	21	17
11	2	1	2	4
12	24	24	24	22
13	9	10	6	11
14	13.5	14	16.5	19.5
15	13.5	15	13	15
16	11	8.5	10.5	9
17	1	22	1	1.5
18	25	25	25	25
19	15	20	18.5	21
20	7	4	8.5	6.5
21	5	5	4	8
22	3	2	3	5
23	20	16.5	14	18
24	22	21	23	23
25	18	19	20	1.5
Dữ liệu từ Pereira AJ, Corrêa TD, de Almeida FP, và cộng sự: Inaccuracy of venous point-of-care glucose measurements in critically ill patients: a cross-sectional study, PLoS One. 2015 Jun 12;10(6):e0129568.

Các hạng của các biến được sử dụng trong phương trình cho hệ số tương quan, và phép tính kết quả cho ra hệ số tương quan hạng Spearman ( $r_{S}$ ), còn được gọi là rho của Spearman:

$r_S = \frac{\sum(R_X - \overline{R}_X)(R_Y - \overline{R}_Y)}{\sqrt{\sum(R_X - \overline{R}_X)^2 \sum(R_Y - \overline{R}_Y)^2}}$

trong đó $R_{X}$ là hạng của biến X, $R_{Y}$ là hạng của biến Y, và $R_{X}$ và $R_{Y}$ lần lượt là hạng trung bình của biến X và Y. Tương quan hạng $r_{S}$ cũng có thể được tính bằng các công thức khác, nhưng quy trình xấp xỉ này khá tốt (Conover và Iman, 1981). Tính toán $r_{S}$ cho các quan sát đã xếp hạng trong Bảng 8-3 cho ra:

$r_{S} = 1299.5 \times 1299.0 998.5 = 0.77$

Giá trị của $r_{S}$ nhỏ hơn giá trị của hệ số tương quan Pearson; điều này có thể xảy ra khi phân phối hai biến của hai biến số không phải là phân phối chuẩn. Kiểm định t, như đã minh họa cho tương quan Pearson, có thể được sử dụng để xác định xem tương quan hạng Spearman có khác không một cách có ý nghĩa thống kê hay không. Ví dụ, quy trình sau đây kiểm định xem giá trị của rho của Spearman trong quần thể, ký hiệu là $ρ_{S}$ (chữ rho Hy Lạp với chỉ số dưới S biểu thị Spearman), có khác không hay không.

Bước 1: $H_{0}$ : Giá trị quần thể của rho của Spearman bằng không; tức là, $ρ_{S} = 0$ . $H_{1}$ : Giá trị quần thể của rho của Spearman khác không; tức là, $ρ_{S} \neq = 0$ .
Bước 2: Vì giả thuyết không là một kiểm định về việc $ρ_{S}$ có bằng không hay không, tỷ số t có thể được sử dụng.
Bước 3: Hãy sử dụng $α = 0.05$ cho ví dụ này.
Bước 4: Bậc tự do là $n - 2 = 25 - 2 = 23$ . Giá trị của phân phối t với 23 bậc tự do chia khu vực thành 95% trung tâm và 2.5% ở mỗi đuôi trên và dưới là 2.069 (Bảng A-3), vì vậy chúng ta sẽ bác bỏ giả thuyết không nếu (giá trị tuyệt đối của) giá trị t quan sát được lớn hơn 2.069.
Bước 5: Phép tính là: $t = \frac{r\sqrt{n-2}}{\sqrt{1-r^2}} = \frac{0.77\sqrt{25-2}}{\sqrt{1-0.77^2}} = 5.53$
Bước 6: Giá trị quan sát được của tỷ số t với 23 bậc tự do là 5.53, lớn hơn 2.069, vì vậy chúng ta bác bỏ giả thuyết không và kết luận có đủ bằng chứng cho thấy tồn tại một mối tương quan phi tham số giữa các phép đo đường huyết được thực hiện bằng xét nghiệm lab và thiết bị đầu ngón tay.

Tất nhiên, nếu các nhà nghiên cứu chỉ muốn kiểm định xem rho của Spearman có lớn hơn không—rằng có một mối quan hệ dương có ý nghĩa—họ có thể sử dụng kiểm định một phía. Đối với kiểm định một phía với $α = 0.05$ và 23 bậc tự do, giá trị tới hạn là 1.714, và kết luận là như nhau.

Tóm lại, rho của Spearman là phù hợp khi các nhà nghiên cứu muốn đo lường mối quan hệ giữa: (1) hai biến thứ bậc, hoặc (2) hai biến định lượng khi một hoặc cả hai không có phân phối chuẩn và các nhà nghiên cứu chọn không sử dụng phép biến đổi dữ liệu (chẳng hạn như lấy logarit). Tương quan hạng Spearman đặc biệt phù hợp khi có các giá trị ngoại lai trong các quan sát.

Khoảng Tin cậy cho Tỷ số Chênh và Nguy cơ Tương đối

Chương 3 đã giới thiệu nguy cơ tương đối (hoặc tỷ số nguy cơ) và tỷ số chênh (odds ratio) là các thước đo mối quan hệ giữa hai đặc tính danh nghĩa. Được phát triển bởi các nhà dịch tễ học, các thống kê này được sử dụng cho các nghiên cứu kiểm tra các nguy cơ có thể dẫn đến bệnh tật. Để thảo luận về tỷ số chênh, hãy nhớ lại nghiên cứu được thảo luận trong Chương 3 của Billioti de Gage và cộng sự (2014) đã kiểm tra việc sử dụng benzodiazepine. Dữ liệu từ nghiên cứu này đã được đưa ra trong Chương 3, Bảng 3-21. Chúng ta đã tính toán tỷ số chênh là 1.5, có nghĩa là một đối tượng trong nhóm sử dụng benzodiazepine có khả năng mắc bệnh Alzheimer cao hơn 1.5 lần so với một đối tượng không phơi nhiễm. Điều quan trọng là phải biết liệu nguy cơ gia tăng này có ý nghĩa thống kê hay không.

Ý nghĩa thống kê có thể được xác định theo nhiều cách. Ví dụ, để kiểm định ý nghĩa của mối quan hệ giữa việc điều trị (phơi nhiễm benzodiazepine) và sự phát triển của bệnh Alzheimer, các nhà nghiên cứu có thể sử dụng kiểm định chi-bình phương đã được thảo luận trong Chương 6. Kiểm định chi-bình phương cho ví dụ này được để lại như một bài tập (xem Bài tập 2). Một kiểm định chi-bình phương thay thế, dựa trên logarit tự nhiên của tỷ số chênh, cũng có sẵn, và nó cho ra các giá trị gần với kiểm định chi-bình phương được minh họa trong Chương 6 (Fleiss, 1999).

Thường xuyên hơn, các bài báo trong y văn sử dụng các khoảng tin cậy cho tỷ số nguy cơ hoặc tỷ số chênh. Billioti de Gage và cộng sự đã báo cáo một khoảng tin cậy 95% cho tỷ số chênh là (1.36-1.69). Hãy xem họ đã tìm ra khoảng tin cậy này như thế nào.

Việc tìm khoảng tin cậy cho tỷ số chênh phức tạp hơn một chút so với thông thường vì các tỷ số này không có phân phối chuẩn, vì vậy các phép tính yêu cầu tìm logarit tự nhiên và đối logarit. Công thức cho khoảng tin cậy 95% cho tỷ số chênh là:

$\exp[\ln(OR) \pm 1.96 \sqrt{\frac{1}{a} + \frac{1}{b} + \frac{1}{c} + \frac{1}{d}}]$

trong đó $exp$ là hàm mũ, hay đối logarit, của logarit tự nhiên, $ln$ , và a, b, c, d là các ô trong bảng $2 \times 2$ (xem Bảng 6-9 trong Chương 6). Khoảng tin cậy cho tỷ số chênh về nguy cơ mắc bệnh Alzheimer đối với các đối tượng phơi nhiễm benzodiazepine từ Bảng 3-19 là:

$\exp[\ln(1.51) \pm 1.96 \sqrt{\frac{1}{894} + \frac{1}{2873} + \frac{1}{902} + \frac{1}{4311}}]$

$\exp[0.412 \pm 1.96 \sqrt{0.003}]$

1.36 đến 1.68

Khoảng này chứa giá trị của tỷ số chênh thực sự với độ tin cậy 95%. Nếu tỷ lệ chênh (odds) là như nhau trong mỗi nhóm, giá trị của tỷ số chênh xấp xỉ 1, cho thấy nguy cơ tương tự trong mỗi nhóm. Vì khoảng này không chứa 1, chúng ta có thể kết luận rằng có đủ bằng chứng để kết luận rằng nguy cơ mắc bệnh Alzheimer tăng lên khi phơi nhiễm với benzodiazepine.

Để minh họa khoảng tin cậy cho nguy cơ tương đối, chúng ta tham khảo nghiên cứu về các triệu chứng cúm của Anderson và cộng sự (2018) được tóm tắt trong Chương 3 và Bảng 3-17. Hãy nhớ lại rằng nguy cơ tương đối cho chẩn đoán cúm ở những bệnh nhân đã tiêm vắc-xin cúm trong 12 tháng qua là 0.616. Khoảng tin cậy 95% cho giá trị thực của nguy cơ tương đối cũng liên quan đến logarit:

$\exp[\ln(RR) \pm 1.96 \sqrt{\frac{1 - [a/(a+b)]}{a} + \frac{1 - [c/(c+d)]}{c}}]$

Một lần nữa, các giá trị a, b, c, d là các ô trong bảng $2 \times 2$ được minh họa trong Bảng 6-9. Mặc dù có thể bao gồm hiệu chỉnh liên tục cho nguy cơ tương đối hoặc tỷ số chênh, điều này không thường được thực hiện. Thay thế các giá trị từ Bảng 3-19, khoảng tin cậy 95% cho nguy cơ tương đối 0.616 là:

0.54 đến 0.70

Khoảng tin cậy 95% không chứa 1, vì vậy bằng chứng cho thấy việc sử dụng vắc-xin cúm đã làm giảm nguy cơ chẩn đoán cúm cho những bệnh nhân có triệu chứng cúm. Để có một cuộc thảo luận chi tiết và sâu sắc về tỷ số chênh và các ưu nhược điểm của nó, xem Feinstein (1985, Chương 20) và Fleiss (1999, Chương 5); để thảo luận về tỷ số chênh và tỷ số nguy cơ, xem Greenberg và cộng sự (2015, Chương 2).

HỒI QUY TUYẾN TÍNH

Hãy nhớ rằng khi mục tiêu là dự đoán giá trị của một đặc tính từ kiến thức về một đặc tính khác, phương pháp thống kê được sử dụng là phân tích hồi quy. Phương pháp này còn được gọi là hồi quy tuyến tính, hồi quy tuyến tính đơn giản, hoặc hồi quy bình phương tối thiểu. Một cái nhìn sơ lược về lịch sử của các thuật ngữ này rất thú vị và làm sáng tỏ bản chất của phân tích hồi quy.

Các khái niệm về tương quan và hồi quy được phát triển bởi Ngài Francis Galton, một người anh em họ của Charles Darwin, người đã nghiên cứu cả toán học và y học vào giữa thế kỷ 19 (Walker, 1931). Galton quan tâm đến di truyền học và muốn hiểu tại sao một quần thể vẫn ít nhiều giữ nguyên qua nhiều thế hệ với con cháu “trung bình” giống với cha mẹ của chúng; tức là, tại sao các thế hệ kế tiếp không trở nên đa dạng hơn. Bằng cách trồng đậu ngọt và quan sát kích thước trung bình của hạt từ các cây mẹ có kích thước khác nhau, ông đã phát hiện ra hồi quy, mà ông gọi là “xu hướng của kiểu hình con trung bình lý tưởng đi chệch khỏi kiểu hình cha mẹ, quay trở lại cái có thể được mô tả một cách sơ bộ và có lẽ công bằng là kiểu hình tổ tiên trung bình.” Hiện tượng này thường được biết đến nhiều hơn với tên gọi hồi quy về giá trị trung bình. Thuật ngữ “tương quan” được Galton sử dụng trong công trình của mình về di truyền học theo nghĩa “đồng tương quan” giữa các đặc tính như chiều cao của cha và con trai. Nhà toán học Karl Pearson sau đó đã tiếp tục xây dựng lý thuyết về tương quan và hồi quy, và hệ số tương quan được đặt theo tên ông vì lý do này.

Thuật ngữ hồi quy tuyến tính đề cập đến thực tế rằng tương quan và hồi quy chỉ đo lường một mối quan hệ đường thẳng, hay tuyến tính, giữa hai biến. Thuật ngữ “hồi quy đơn giản” có nghĩa là chỉ có một biến giải thích (độc lập) được sử dụng để dự đoán một kết quả. Trong hồi quy đa biến, nhiều hơn một biến độc lập được bao gồm trong phương trình dự đoán.

Hồi quy bình phương tối thiểu mô tả phương pháp toán học để có được phương trình hồi quy. Điều quan trọng cần nhớ là khi thuật ngữ “hồi quy” được sử dụng một mình, nó thường có nghĩa là hồi quy tuyến tính dựa trên phương pháp bình phương tối thiểu. Khái niệm đằng sau hồi quy bình phương tối thiểu được mô tả trong phần tiếp theo và ứng dụng của nó được thảo luận trong phần sau đó.

Phương pháp Bình phương Tối thiểu

Nhiều lần trước đây trong chương này, chúng ta đã đề cập đến bản chất tuyến tính của dạng phân bố các điểm trong một biểu đồ phân tán. Ví dụ, trong Hình 8-2, một đường thẳng có thể được vẽ qua các điểm đại diện cho các giá trị của BMI và tỷ lệ mỡ cơ thể để chỉ ra hướng của mối quan hệ. Phương pháp bình phương tối thiểu là một cách để xác định phương trình của đường thẳng cung cấp sự phù hợp tốt với các điểm.

Để minh họa phương pháp, hãy xem xét đường thẳng trong Hình 8-6. Hình học sơ cấp có thể được sử dụng để xác định phương trình cho bất kỳ đường thẳng nào. Nếu điểm mà đường thẳng cắt, hoặc chặn, trục Y được ký hiệu là a và độ dốc của đường thẳng là b, thì phương trình là:

$Y = a + b X$

Độ dốc của đường thẳng đo lường lượng Y thay đổi mỗi khi X thay đổi 1 đơn vị. Nếu độ dốc là dương, Y tăng khi X tăng; nếu độ dốc là âm, Y giảm khi X tăng; và ngược lại. Trong mô hình hồi quy, độ dốc trong quần thể thường được ký hiệu là $β_{1}$ , được gọi là hệ số hồi quy; và $β_{0}$ ký hiệu cho hệ số chặn của đường hồi quy, tức là, $β_{1}$ và $β_{0}$ là các tham số quần thể trong hồi quy. Trong hầu hết các ứng dụng, các điểm không nằm chính xác trên một đường thẳng. Vì lý do này, mô hình hồi quy chứa một thành phần sai số, $ϵ$ , là khoảng cách mà các giá trị thực tế của Y lệch khỏi đường hồi quy. Gộp tất cả lại, phương trình hồi quy được cho bởi:

$Y = β_{0} + β_{1} X + ϵ$

Khi phương trình hồi quy được sử dụng để mô tả mối quan hệ trong mẫu, nó thường được viết là:

$Y^{'} = b_{0} + b_{1} X$ hoặc $Y^{'} = a + b X$

Trong đó $Y^{'}$ là ký hiệu cho giá trị dự đoán của Y dựa trên một giá trị quan sát X. Đối với một giá trị cho trước của X, chẳng hạn $X^{*}$ , giá trị dự đoán của $Y^{*}$ được tìm thấy bằng cách kéo một đường ngang từ đường hồi quy đến trục Y như trong Hình 8-7. Sự khác biệt giữa giá trị thực tế của $Y^{*}$ và giá trị dự đoán, $e^{*} = Y^{*} - Y^{*'}$ , có thể được sử dụng để đánh giá mức độ phù hợp của đường thẳng với các điểm dữ liệu. Phương pháp bình phương tối thiểu xác định đường thẳng mà tối thiểu hóa tổng bình phương các chênh lệch theo chiều dọc giữa các giá trị thực tế và giá trị dự đoán của biến Y; tức là, $β_{0}$ và $β_{1}$ được xác định sao cho $Σ (Y - Y^{'})^{2}$ là nhỏ nhất. Các công thức cho $β_{0}$ và $β_{1}$ được tìm ra, và theo các ước tính mẫu b và a, các công thức này là:

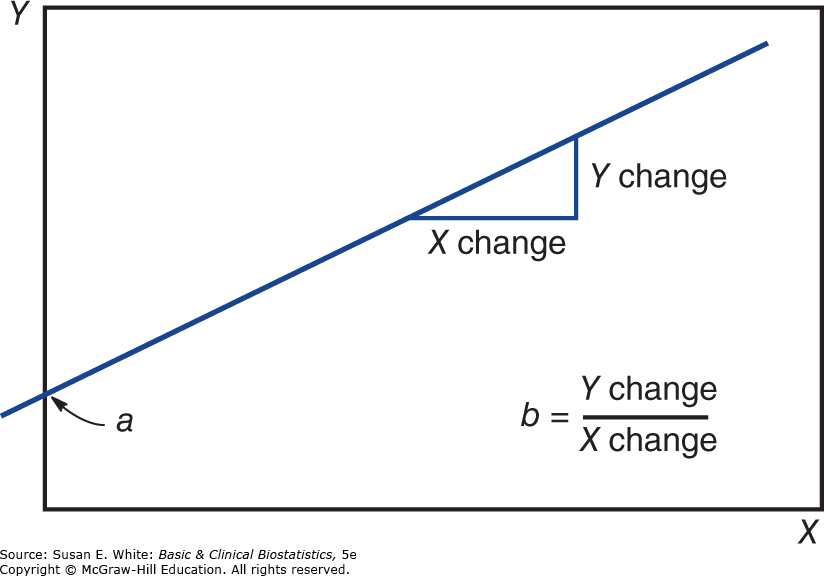
$b = \frac{\Sigma(X - \overline{X})(Y - \overline{Y})}{\Sigma(X - \overline{X})^2}$
$a = \overline{Y} - b\overline{X}$

Hình 8-6. Diễn giải hình học của một đường hồi quy.

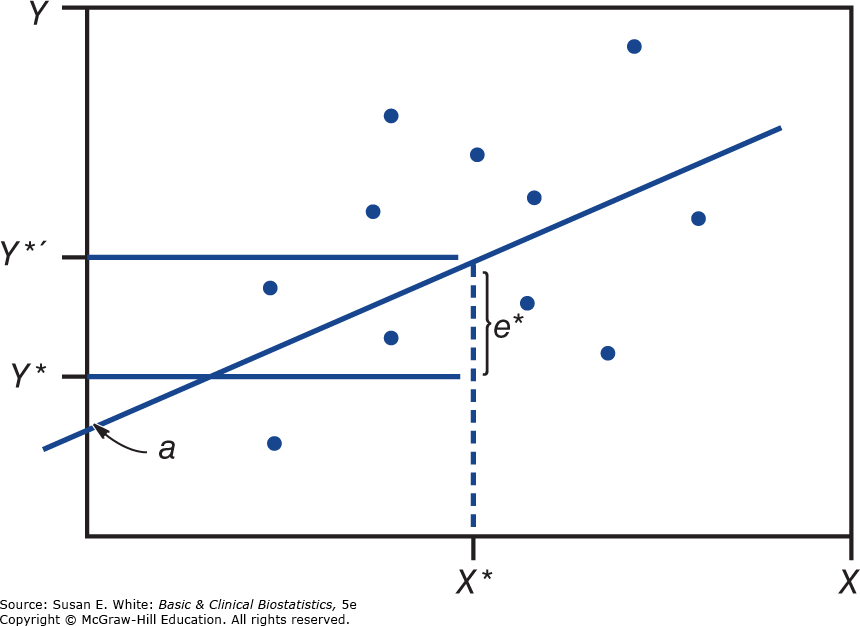
Hình 8-7. Đường hồi quy bình phương tối thiểu.

Tính toán Phương trình Hồi quy

Giả sử chúng ta muốn khớp một đường hồi quy với dữ liệu được hiển thị trong Hình 8-2. Mô hình này có thể được sử dụng để dự đoán tỷ lệ mỡ cơ thể nếu biết BMI của đối tượng.

Trước khi tính toán phương trình hồi quy cho dữ liệu này, hãy xem lại biểu đồ phân tán trong Hình 8-2 và thực hành “đoán” giá trị của hệ số tương quan từ biểu đồ (mặc dù rất khó để ước tính chính xác độ lớn của r khi cỡ mẫu nhỏ). Hình 8-2 là một biểu đồ phân tán với điểm BMI là biến giải thích X và tỷ lệ mỡ cơ thể là biến đáp ứng Y. Từ các tính toán trước, chúng ta biết rằng hệ số tương quan là 0.42.

Vì chúng ta biết hệ số tương quan giữa BMI và tỷ lệ mỡ cơ thể là dương, chúng ta biết rằng độ dốc của đường hồi quy cũng là dương. Dưới đây là các thuật ngữ cần thiết để tính toán độ dốc và hệ số chặn của đường hồi quy:

$\Sigma(X - \overline{X})(Y - \overline{Y}) = 1523.32$
$\Sigma(X - \overline{X})^2 = 1577.02$
$\overline{X} = 23.08$ và $\overline{Y} = 28.34$

Khi đó,

$b = \frac{\Sigma(X - \overline{X})(Y - \overline{Y})}{\Sigma(X - \overline{X})^2} = \frac{1523.32}{1577.02} = 0.97$
$a = \overline{Y} - b\overline{X} = 28.34 - 0.97 \times 23.08 = 5.15$

Trong ví dụ này, tỷ lệ mỡ cơ thể được cho là được hồi quy theo điểm BMI, và phương trình hồi quy được viết là $Y^{'} = 5.15 + 0.97 X$ , trong đó $Y^{'}$ là tỷ lệ mỡ cơ thể dự đoán, và X là BMI quan sát được.

Hình 8-8 minh họa đường hồi quy được vẽ qua các quan sát. Phương trình hồi quy có hệ số chặn dương là +5.15, do đó về mặt lý thuyết, một bệnh nhân có BMI bằng không sẽ có độ nhạy insulin là 5.15, mặc dù trong ví dụ hiện tại, BMI bằng không là không thể. Độ dốc +0.97 cho thấy mỗi khi BMI tăng 1, tỷ lệ mỡ cơ thể dự đoán tăng khoảng 0.97. Ví dụ, khi BMI tăng từ 20 lên 30, tỷ lệ mỡ cơ thể dự đoán tăng từ khoảng 24.55 lên khoảng 34.25. Liệu mối quan hệ giữa BMI và tỷ lệ mỡ cơ thể có ý nghĩa thống kê hay không sẽ được thảo luận trong phần tiếp theo.

Hình 8-8. Hồi quy của các quan sát về chỉ số khối cơ thể và tỷ lệ mỡ cơ thể. (Chuyển thể với sự cho phép từ Neidert LE, Wainright KS, Zheng C, và cộng sự: Plasma dipeptidyl peptidase IV activity and measures of body composition in apparently healthy people, Heliyon. 2016 Apr 18;2(4):e00097.)

Các giả định & Suy luận trong Hồi quy

Trong phần trước, chúng ta đã làm việc với một mẫu quan sát thay vì toàn bộ quần thể quan sát. Giống như trung bình mẫu $X$ là một ước tính của trung bình quần thể $μ$ , đường hồi quy được xác định từ các công thức cho a và b trong phần trước là một ước tính của phương trình hồi quy cho quần thể cơ sở.

Như trong Chương 6 và 7, nơi chúng ta đã sử dụng các kiểm định thống kê để xác định khả năng các khác biệt quan sát được giữa hai giá trị trung bình xảy ra do ngẫu nhiên, trong phân tích hồi quy, chúng ta phải thực hiện các kiểm định thống kê để xác định khả năng của bất kỳ mối quan hệ quan sát được nào giữa các biến X và Y. Một lần nữa, câu hỏi có thể được tiếp cận theo hai cách: sử dụng kiểm định giả thuyết hoặc tạo khoảng tin cậy. Tuy nhiên, trước khi thảo luận về các cách tiếp cận này, chúng ta sẽ thảo luận ngắn gọn về các giả định cần thiết trong phân tích hồi quy.

Nếu chúng ta muốn sử dụng một phương trình hồi quy, các quan sát phải có những thuộc tính nhất định. Do đó, đối với mỗi giá trị của biến X, biến Y được giả định có phân phối chuẩn, và giá trị trung bình của phân phối được giả định là giá trị dự đoán, $Y^{'}$ . Ngoài ra, bất kể giá trị của biến X là gì, độ lệch chuẩn của Y được giả định là như nhau. Những giả định này khá giống như việc tưởng tượng một số lượng lớn các phân phối chuẩn riêng lẻ của biến Y, tất cả đều có cùng kích thước, một cho mỗi giá trị của X. Giả định về sự biến thiên bằng nhau này của Y trên toàn bộ phạm vi của X được gọi là tính đồng nhất, hay homoscedasticity. Nó tương tự như giả định về phương sai bằng nhau (phương sai đồng nhất) trong kiểm định t cho các nhóm độc lập, như đã thảo luận trong Chương 6.

Giả định đường thẳng, hay tuyến tính, yêu cầu rằng các giá trị trung bình của Y tương ứng với các giá trị khác nhau của X nằm trên một đường thẳng. Các giá trị của Y được giả định là độc lập với nhau. Giả định này không được đáp ứng khi các phép đo lặp lại được thực hiện trên cùng một đối tượng; tức là, một phép đo của một đối tượng tại một thời điểm không độc lập với phép đo của cùng đối tượng đó tại một thời điểm khác. Cuối cùng, như với các quy trình thống kê khác, chúng ta giả định các quan sát tạo thành một mẫu ngẫu nhiên từ quần thể quan tâm.

Hồi quy là một quy trình mạnh mẽ và có thể được sử dụng trong nhiều tình huống mà các giả định không được đáp ứng, miễn là các phép đo khá đáng tin cậy và mô hình hồi quy chính xác được sử dụng. (Các mô hình hồi quy khác được thảo luận trong Chương 10.) Việc đáp ứng các giả định hồi quy thường gây ra ít vấn đề hơn trong các thí nghiệm hoặc thử nghiệm lâm sàng so với trong các nghiên cứu quan sát vì độ tin cậy của các phép đo có xu hướng cao hơn trong các nghiên cứu thực nghiệm. Tuy nhiên, các quy trình đặc biệt có thể được sử dụng khi các giả định bị vi phạm nghiêm trọng; và như trong ANOVA, các nhà nghiên cứu nên tìm kiếm lời khuyên của một nhà thống kê trước khi sử dụng hồi quy nếu có câu hỏi về khả năng áp dụng của nó.

Sai số Chuẩn của Ước lượng: Các đường hồi quy, giống như các thống kê khác, có thể thay đổi. Rốt cuộc, phương trình hồi quy được tính toán cho bất kỳ một mẫu quan sát nào chỉ là một ước tính của phương trình hồi quy quần thể thực sự. Nếu các mẫu khác được chọn từ quần thể và một phương trình hồi quy được tính toán cho mỗi mẫu, các phương trình này sẽ thay đổi từ mẫu này sang mẫu khác về cả độ dốc và hệ số chặn của chúng. Một ước tính của sự biến thiên này được ký hiệu là $S_{Y . X}$ (đọc là s của y cho trước x) và được gọi là sai số chuẩn của hồi quy, hoặc sai số chuẩn của ước lượng. Nó dựa trên bình phương độ lệch của các giá trị Y dự đoán so với các giá trị Y thực tế và được tìm thấy như sau:

$S_{Y.X} = \sqrt{\frac{\Sigma(Y - Y')^2}{n-2}}$

Việc tính toán công thức này khá tẻ nhạt; và mặc dù có các dạng tính toán thân thiện hơn với người dùng, chúng tôi giả định rằng bạn sẽ sử dụng một chương trình máy tính để tính toán sai số chuẩn của ước lượng. Trong việc kiểm định cả độ dốc và hệ số chặn, một kiểm định t có thể được sử dụng, và sai số chuẩn của ước lượng là một phần của công thức. Nó cũng được sử dụng trong việc xác định các giới hạn tin cậy. Để trình bày các công thức này và logic liên quan đến việc kiểm định độ dốc và hệ số chặn, chúng tôi minh họa kiểm định giả thuyết cho hệ số chặn và tính toán khoảng tin cậy cho độ dốc, sử dụng phương trình hồi quy BMI-tỷ lệ mỡ cơ thể.

Suy luận về Hệ số Chặn: Để kiểm định giả thuyết rằng hệ số chặn khác không một cách có ý nghĩa, chúng ta sử dụng quy trình sau:

Bước 1: $H_{0} : β_{0} = 0$ (Hệ số chặn bằng không) $H_{1} : β_{0} \neq = 0$ (Hệ số chặn khác không)
Bước 2: Vì giả thuyết không là một kiểm định về việc hệ số chặn có bằng không hay không, tỷ số t có thể được sử dụng nếu các giả định được đáp ứng. Tỷ số t sử dụng sai số chuẩn của ước lượng để tính sai số chuẩn của hệ số chặn (mẫu số của tỷ số t):
$t = \frac{a - \beta_0}{\sqrt{S_{Y.X}^2 \{ (1/n) + [\overline{X}^2 / \Sigma(X - \overline{X})^2] \}}}$
Bước 3: Hãy sử dụng $α$ bằng 0.05.
Bước 4: Bậc tự do là $n - 2 = 111 - 2 = 109$ . Giá trị của phân phối t với 109 bậc tự do chia khu vực thành 95% trung tâm và 5% ở hai đuôi trên và dưới là khoảng 1.98 (từ Bảng A-3). Do đó, chúng ta bác bỏ giả thuyết không về hệ số chặn bằng không nếu (giá trị tuyệt đối của) giá trị t quan sát được lớn hơn 1.98.
Bước 5: Phép tính như sau; chúng tôi đã sử dụng một bảng tính (Microsoft Excel) để tính $S_{Y.X} = 7.98$ và $\Sigma(X - \overline{X})^2 = 1577.02$
$t = \frac{5.15 - 0}{\sqrt{7.98^2 (1/111 + [23.08^2 / 1577.02])}} = \frac{5.15}{\sqrt{23.47}} = 1.06$
Bước 6: Giá trị tuyệt đối của tỷ số quan sát được là 1.06, không lớn hơn 1.98. Do đó, giả thuyết không về hệ số chặn bằng không không bị bác bỏ. Chúng ta kết luận rằng không đủ bằng chứng để cho thấy hệ số chặn khác không một cách có ý nghĩa đối với hồi quy của tỷ lệ mỡ cơ thể theo BMI.

Như bạn đã biết, cũng có thể tạo các giới hạn tin cậy cho hệ số chặn bằng cách sử dụng giá trị quan sát được và cộng hoặc trừ giá trị tới hạn từ phân phối t nhân với sai số chuẩn của hệ số chặn.

Suy luận về Hệ số Hồi quy: Thay vì minh họa kiểm định giả thuyết cho hệ số hồi quy quần thể, hãy tìm một khoảng tin cậy 95% cho $β_{1}$ . Khoảng này được cho bởi:

$b \pm t_{n-2} \sqrt{S_{Y.X}^2 [\frac{1}{\Sigma(X - \overline{X})^2}]}$
$= 0.97 \pm 1.98 \sqrt{7.98^2 (\frac{1}{1577.02})}$
$= 0.97 \pm 0.40$ hay 0.57 đến 1.37

Vì khoảng này không bao gồm số không, chúng ta có thể tin tưởng 95% rằng hệ số hồi quy không bằng không mà nằm trong khoảng từ 0.57 đến 1.37. Vì hệ số hồi quy lớn hơn không một cách có ý nghĩa, liệu hệ số tương quan có thể bằng không không? (Xem Bài tập 2.) Mối quan hệ giữa b và r được minh họa trước đó và Bài tập 2 sẽ thuyết phục bạn về sự tương đương của các kết quả thu được khi kiểm định ý nghĩa của tương quan và hệ số hồi quy. Thực tế, các tác giả trong y văn thường thực hiện một phân tích hồi quy và sau đó báo cáo các giá trị P để chỉ ra một hệ số tương quan có ý nghĩa.

Kết quả từ chương trình hồi quy R được đưa ra trong Bảng 8-4. Chương trình tạo ra giá trị t và giá trị P liên quan, cũng như các giới hạn tin cậy 95%. Các kết quả có khớp với những gì chúng ta đã tìm thấy trước đó không? Để làm quen với việc sử dụng hồi quy, chúng tôi đề nghị bạn tái tạo các kết quả này bằng cách sử dụng tệp dữ liệu và R.

Bảng 8-4. Kết quả hồi quy tỷ lệ mỡ cơ thể theo chỉ số khối cơ thể (BMI)

Phần 1: Hệ số hồi quy

Biến số	Ước tính (Hệ số)	Sai số chuẩn	Giá trị t	Mức ý nghĩa (P)
(Hệ số chặn)	5.1539	4.8438	1.064	0.29
BMI (kg/m²)	0.9742	0.2010	4.847	< 0.0001***

Phần 2: Khoảng tin cậy 95% cho các hệ số

Biến số	Ước tính	Giới hạn dưới (2.5%)	Giới hạn trên (97.5%)
(Hệ số chặn)	5.1539	-4.4464	14.7542
BMI (kg/m²)	0.9742	0.5758	1.3725

Dự đoán bằng Phương trình Hồi quy: Giá trị Cá nhân và Trung bình: Một trong những lý do quan trọng để có được một phương trình hồi quy là để dự đoán các giá trị trong tương lai cho một nhóm đối tượng (hoặc cho các đối tượng cá nhân). Ví dụ, một bác sĩ lâm sàng có thể muốn dự đoán tỷ lệ mỡ cơ thể từ BMI cho một nhóm người tham gia vào một chế độ thể dục mới. Hoặc bác sĩ lâm sàng có thể muốn dự đoán tỷ lệ mỡ cơ thể cho một bệnh nhân cụ thể. Trong cả hai trường hợp, sự biến thiên liên quan đến đường hồi quy phải được phản ánh trong dự đoán.

Khoảng tin cậy 95% cho một giá trị trung bình Y dự đoán trong một nhóm đối tượng là:

$\text{Trung bình } Y' \pm t_{(n-2)} \sqrt{S_{Y.X}^2 [\frac{1}{n} + \frac{(X - \overline{X})^2}{\Sigma(X - \overline{X})^2}]}$

Khoảng tin cậy 95% để dự đoán một quan sát đơn lẻ là:

$Y' \pm t_{(n-2)} \sqrt{S_{Y.X}^2 [1 + \frac{1}{n} + \frac{(X - \overline{X})^2}{\Sigma(X - \overline{X})^2}]}$

So sánh hai công thức này, chúng ta thấy rằng khoảng tin cậy dự đoán một quan sát đơn lẻ rộng hơn khoảng tin cậy cho giá trị trung bình của một nhóm cá nhân; 1 được cộng vào thành phần sai số chuẩn cho trường hợp cá nhân. Kết quả này hợp lý, vì đối với một giá trị cho trước của X, sự biến thiên trong điểm số của các cá nhân lớn hơn sự biến thiên trong điểm số trung bình của các nhóm cá nhân. Cũng lưu ý rằng tử số của thành phần thứ ba trong sai số chuẩn là bình phương độ lệch của X so với $X$ . Do đó, độ lớn của sai số chuẩn phụ thuộc vào mức độ gần của quan sát so với giá trị trung bình; X càng gần giá trị trung bình của nó, dự đoán Y càng chính xác. Đối với các giá trị X khá xa giá trị trung bình, sự biến thiên trong việc dự đoán điểm Y là đáng kể. Bạn có thể hiểu tại sao các nhà kinh tế và những người khác muốn dự đoán các sự kiện trong tương lai lại khó có thể rất chính xác!

Bảng 8-5 cung cấp các khoảng tin cậy 95% liên quan đến tỷ lệ mỡ cơ thể trung bình dự đoán và tỷ lệ mỡ cơ thể dự đoán cho một cá nhân tương ứng với một số giá trị BMI khác nhau. Một số hiểu biết về phân tích hồi quy có thể được thu thập bằng cách kiểm tra bảng này. Đầu tiên, lưu ý sự khác biệt về độ lớn giữa các sai số chuẩn liên quan đến tỷ lệ mỡ cơ thể trung bình dự đoán và những sai số liên quan đến tỷ lệ mỡ cơ thể cá nhân: các sai số chuẩn lớn hơn nhiều khi chúng ta dự đoán các giá trị cá nhân so với khi chúng ta dự đoán giá trị trung bình. Thực tế, sai số chuẩn cho các cá nhân luôn lớn hơn sai số chuẩn cho các giá trị trung bình vì có thêm số 1 trong công thức. Cũng lưu ý rằng các sai số chuẩn có giá trị nhỏ nhất khi quan sát quan tâm gần với giá trị trung bình (BMI là 23.80 trong ví dụ của chúng ta). Khi quan sát lệch khỏi giá trị trung bình theo cả hai hướng, các sai số chuẩn và khoảng tin cậy ngày càng lớn hơn, phản ánh bình phương chênh lệch giữa quan sát và giá trị trung bình. Nếu các khoảng tin cậy được vẽ dưới dạng dải tin cậy quanh đường hồi quy, chúng sẽ gần nhất với đường thẳng tại giá trị trung bình của X và cong ra xa nó theo cả hai hướng ở mỗi bên của $X$ . Hình 8-9 cho thấy biểu đồ của các dải tin cậy.

Bảng 8-5. Khoảng tin cậy 95% cho tỷ lệ mỡ cơ thể trung bình dự đoán và tỷ lệ mỡ cơ thể cá nhân dự đoán.

BMI	Tỷ lệ mỡ cơ thể	Dự đoán	$S E^{a}$	Khoảng tin cậy (Trung bình)	$S E^{b}$	Khoảng tin cậy (Cá nhân)
19.30	32.60	23.87	1.180	21.53 đến 26.21	8.069	7.89 đến 39.85
20.00	25.90	24.55	1.076	22.42 đến 26.68	8.054	8.6 đến 40.5
20.80	30.00	25.33	0.969	23.41 đến 27.24	8.041	9.41 đến 41.25
21.00	34.60	25.52	0.944	23.65 đến 27.39	8.038	9.61 đến 41.43
23.00	26.60	27.46	0.775	25.93 đến 28.99	8.020	11.58 đến 43.34
23.20	40.60	27.65	0.767	26.13 đến 29.17	8.019	11.78 đến 43.53
25.80	37.30	30.18	0.857	28.48 đến 31.87	8.028	14.28 đến 46.07
26.60	38.90	30.95	0.943	29.08 đến 32.82	8.038	15.04 đến 46.87
27.80	34.00	32.12	1.104	29.93 đến 34.3	8.058	16.16 đến 48.07
30.70	33.60	34.93	1.580	31.8 đến 38.06	8.137	18.82 đến 51.04
23.80	35.30	28.24	0.758	26.74 đến 29.74	8.018	12.36 đến 44.11
BMI, chỉ số khối cơ thể.
$^{a}$ Sai số chuẩn cho trung bình.
$^{b}$ Sai số chuẩn cho cá nhân.

Bảng 8-5 minh họa một đặc điểm thú vị khác của phương trình hồi quy (dòng được in đậm). Khi giá trị trung bình của X được sử dụng trong phương trình hồi quy, giá trị $Y^{'}$ dự đoán là giá trị trung bình của Y. Do đó, đường hồi quy đi qua giá trị trung bình của X và giá trị trung bình của Y.

Bây giờ chúng ta có thể thấy tại sao các dải tin cậy quanh đường hồi quy lại cong. Sai số trong hệ số chặn có nghĩa là đường hồi quy thực sự có thể nằm trên hoặc dưới đường được tính toán cho các quan sát mẫu, mặc dù nó vẫn duy trì cùng hướng (độ dốc). Do đó, sai số trong việc đo lường độ dốc có nghĩa là đường hồi quy thực sự có thể xoay quanh điểm $(X, Y)$ đến một mức độ nhất định. Sự kết hợp của hai sai số này dẫn đến các dải tin cậy lõm được minh họa trong Hình 8-9. Đôi khi các bài báo khoa học có các đường hồi quy với các dải tin cậy song song thay vì cong. Các dải tin cậy này là không chính xác, mặc dù chúng có thể tương ứng với các sai số chuẩn hoặc các khoảng tin cậy tại khoảng cách hẹp nhất của chúng so với đường hồi quy.

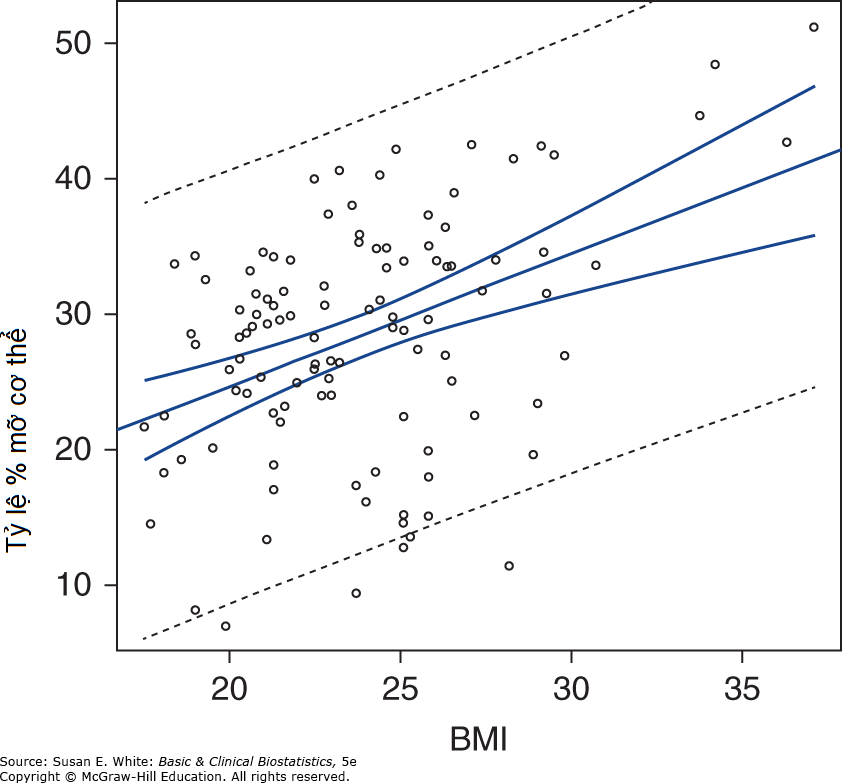
Hình 8-9. Hồi quy của các quan sát về chỉ số khối cơ thể và tỷ lệ mỡ cơ thể với các dải tin cậy (đường đậm cho trung bình, đường nhạt cho cá nhân). (Chuyển thể với sự cho phép từ Neidert LE, Wainright KS, Zheng C, và cộng sự: Plasma dipeptidyl peptidase IV activity and measures of body composition in apparently healthy people, Heliyon. 2016 Apr 18;2(4):e00097.)

So sánh Hai Đường Hồi quy

Đôi khi các nhà nghiên cứu muốn so sánh hai đường hồi quy để xem chúng có giống nhau hay không. Ví dụ, các nhà nghiên cứu trong vấn đề trước đó có thể quan tâm đến mối quan hệ giữa BMI và tỷ lệ mỡ cơ thể ở nam và nữ. Các đường hồi quy cho mỗi giới tính được hiển thị trong Hình 8-10.

Như bạn có thể đoán, các nhà nghiên cứu thường quan tâm đến việc so sánh các đường hồi quy để tìm hiểu xem các mối quan hệ có giống nhau trong các nhóm đối tượng khác nhau hay không. Khi chúng ta so sánh hai đường hồi quy, bốn tình huống có thể xảy ra, như được minh họa trong Hình 8-11. Trong Hình 8-11A, độ dốc của các đường hồi quy là như nhau, nhưng hệ số chặn khác nhau. Tình huống này xảy ra, ví dụ, trong Hình 8-10 khi tỷ lệ mỡ cơ thể được hồi quy theo BMI ở nam và nữ; tức là, mối quan hệ giữa tỷ lệ mỡ cơ thể và BMI là tương tự đối với nam và nữ (độ dốc bằng nhau), nhưng nam giới có xu hướng có mức mỡ cơ thể thấp hơn ở mọi mức BMI so với nữ giới (hệ số chặn thấp hơn đối với nam).

Trong Hình 8-11B, các hệ số chặn bằng nhau, nhưng độ dốc khác nhau. Mô hình này có thể mô tả, chẳng hạn, hồi quy của số lượng tiểu cầu theo số ngày sau khi cấy ghép tủy xương ở hai nhóm bệnh nhân: những người mà liệu pháp bổ trợ dẫn đến thuyên giảm bệnh nền và những người mà bệnh vẫn còn hoạt động. Nói cách khác, trước và ngay sau khi cấy ghép, số lượng tiểu cầu là tương tự cho cả hai nhóm (hệ số chặn bằng nhau), nhưng tại một thời điểm nào đó sau khi cấy ghép, số lượng tiểu cầu vẫn ổn định đối với bệnh nhân thuyên giảm và bắt đầu giảm đối với bệnh nhân không thuyên giảm (độ dốc âm hơn đối với bệnh nhân có bệnh hoạt động).

Trong Hình 8-11C, cả hệ số chặn và độ dốc của các đường hồi quy đều khác nhau. Mặc dù họ không đề cập cụ thể đến bất kỳ sự khác biệt nào về hệ số chặn, mối quan hệ giữa BMI và tỷ lệ mỡ cơ thể giống với tình huống trong Hình 8-11A.

Nếu không có sự khác biệt nào trong các mối quan hệ giữa các biến dự đoán và biến kết quả, các đường hồi quy sẽ tương tự như Hình 8-11D, trong đó các đường trùng nhau: cả hệ số chặn và độ dốc đều bằng nhau. Tình huống này xảy ra trong nhiều tình huống trong y học và được coi là mô hình dự kiến (giả thuyết không) cho đến khi được chứng minh là không áp dụng bằng cách kiểm định giả thuyết hoặc tạo giới hạn tin cậy cho hệ số chặn và/hoặc độ dốc (hoặc cả hệ số chặn và độ dốc).

Từ bốn tình huống được minh họa trong Hình 8-11, chúng ta có thể thấy rằng có ba câu hỏi thống kê cần được đặt ra:

Các độ dốc có bằng nhau không?
Các hệ số chặn có bằng nhau không?
Cả độ dốc và hệ số chặn có bằng nhau không?

Các kiểm định thống kê dựa trên phân phối t có thể được sử dụng để trả lời hai câu hỏi đầu tiên; các kiểm định này được minh họa trong Kleinbaum và Klein (2010). Tuy nhiên, các tác giả chỉ ra rằng cách tiếp cận ưu tiên là sử dụng các mô hình hồi quy cho nhiều hơn một biến độc lập—một quy trình được gọi là hồi quy đa biến—để trả lời những câu hỏi này. Quy trình bao gồm việc gộp các quan sát từ cả hai mẫu đối tượng (ví dụ: quan sát trên cả nam và nữ) và tính toán một đường hồi quy cho dữ liệu kết hợp. Các hệ số hồi quy khác cho biết liệu việc các quan sát thuộc nhóm nào có quan trọng hay không. Sau đó, mô hình đơn giản nhất được chọn.

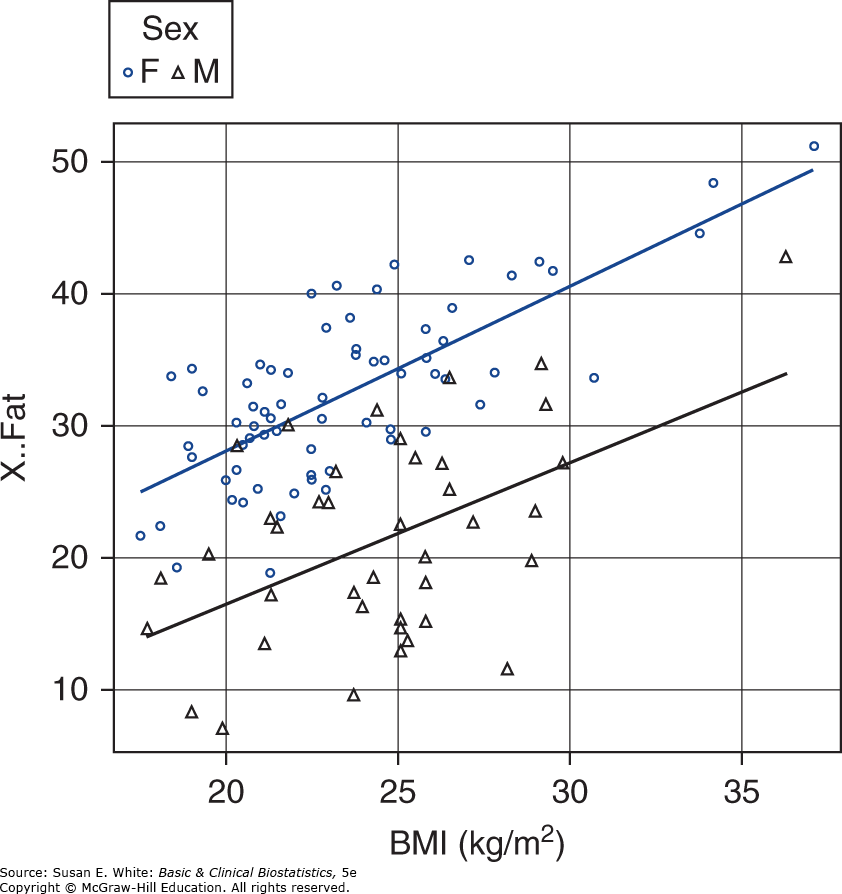
Hình 8-10. Các đường hồi quy riêng biệt cho nam (tam giác) và nữ (vòng tròn). (Chuyển thể với sự cho phép từ Neidert LE, Wainright KS, Zheng C, và cộng sự: Plasma dipeptidyl peptidase IV activity and measures of body composition in apparently healthy people, Heliyon. 2016 Apr 18;2(4):e00097.)

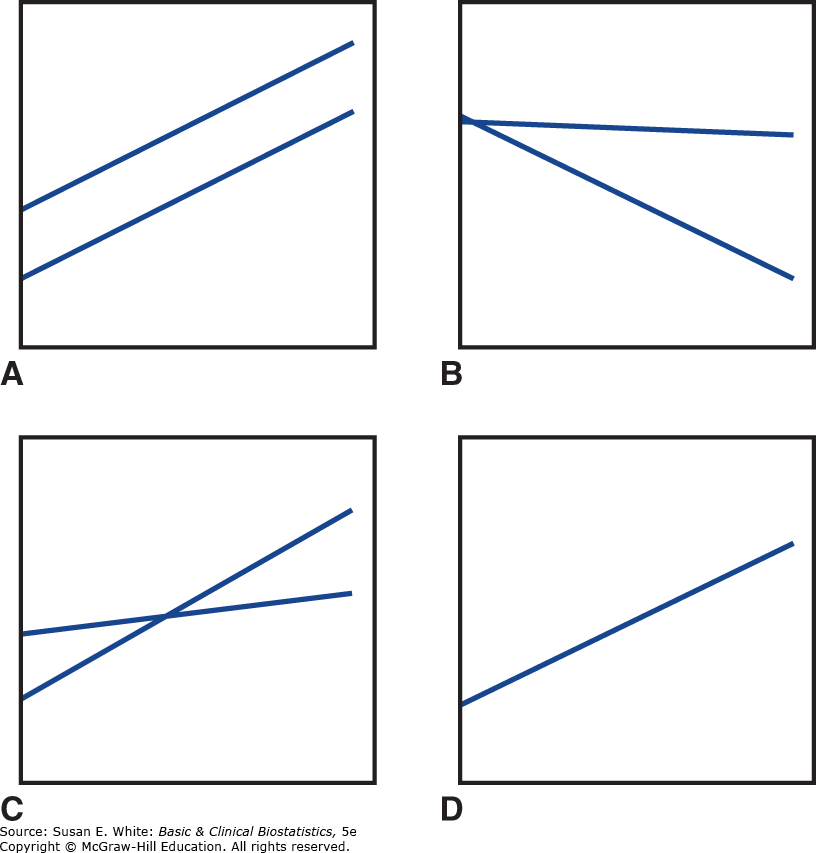
Hình 8-11. Minh họa các cách các đường hồi quy có thể khác nhau. A: Độ dốc bằng nhau và hệ số chặn khác nhau. B: Hệ số chặn bằng nhau và độ dốc khác nhau. C: Độ dốc khác nhau và hệ số chặn khác nhau. D: Độ dốc bằng nhau và hệ số chặn bằng nhau.

SỬ DỤNG TƯƠNG QUAN & HỒI QUY

Một số đặc điểm của tương quan và hồi quy đã được lưu ý trong suốt các cuộc thảo luận trong chương này, và chúng tôi tóm tắt lại chúng ở đây cũng như đề cập đến các đặc điểm khác. Một điểm quan trọng cần nhấn mạnh lại là tương quan và hồi quy chỉ mô tả các mối quan hệ tuyến tính. Nếu các hệ số tương quan hoặc phương trình hồi quy được tính toán một cách mù quáng, mà không kiểm tra các biểu đồ của dữ liệu, các nhà nghiên cứu có thể bỏ lỡ các mối quan hệ rất mạnh nhưng phi tuyến.

Phân tích Phần dư

Một quy trình hữu ích trong việc đánh giá sự phù hợp của phương trình hồi quy là phân tích phần dư (Pedhazur, 1997). Chúng ta đã tính toán phần dư khi chúng ta tìm thấy sự khác biệt giữa giá trị thực tế của Y và giá trị dự đoán của $Y^{'}$ , hay $Y - Y^{'}$ , mặc dù chúng ta không sử dụng thuật ngữ này. Phần dư là phần của Y không được dự đoán bởi X (phần còn lại, hoặc phần dư). Các giá trị phần dư trên trục Y được vẽ so với các giá trị X trên trục X. Giá trị trung bình của các phần dư bằng không, và, vì độ dốc đã được trừ đi trong quá trình tính toán phần dư, tương quan giữa chúng và các giá trị X phải bằng không.

Nói cách khác, nếu mô hình hồi quy cung cấp một sự phù hợp tốt với dữ liệu, như trong Hình 8-12A, các giá trị của phần dư không liên quan đến các giá trị của X. Một biểu đồ của phần dư và các giá trị X trong tình huống này sẽ giống như một sự phân tán các điểm tương ứng với Hình 8-12B, trong đó không có tương quan nào tồn tại giữa các phần dư và các giá trị của X. Ngược lại, nếu một mối quan hệ cong xảy ra giữa Y và X, như trong Hình 8-12C, các phần dư là âm cho cả các giá trị nhỏ và lớn của X, vì các giá trị tương ứng của Y nằm dưới một đường hồi quy được vẽ qua dữ liệu. Tuy nhiên, chúng là dương cho các giá trị X cỡ trung bình vì các giá trị tương ứng của Y nằm trên đường hồi quy. Trong trường hợp này, thay vì có được một sự phân tán ngẫu nhiên, chúng ta có một biểu đồ giống như đường cong trong Hình 8-12D, với các giá trị của phần dư liên quan đến các giá trị của X. Các mẫu khác có thể được các nhà thống kê sử dụng để giúp chẩn đoán các vấn đề, chẳng hạn như thiếu phương sai bằng nhau hoặc các loại phi tuyến tính khác nhau.

Hãy sử dụng tệp dữ liệu và R để tạo một biểu đồ phần dư cho dữ liệu trong Neidert và cộng sự (2016). Tình huống nào trong bốn tình huống trong Hình 8-12 là có khả năng nhất? Xem Bài tập 8.

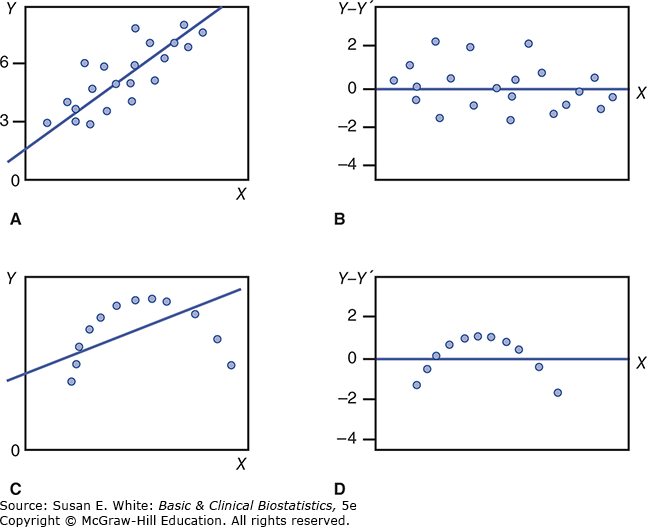
Hình 8-12. Minh họa phân tích phần dư. A: Mối quan hệ tuyến tính giữa X và Y. B: Phần dư so với các giá trị của X cho mối quan hệ trong phần A. C: Mối quan hệ cong giữa X và Y. D: Phần dư so với các giá trị của X cho mối quan hệ trong phần C.

Xử lý các Quan sát Phi tuyến

Một số hành động thay thế có thể được thực hiện nếu các vấn đề nghiêm trọng phát sinh với tính phi tuyến của dữ liệu. Như chúng ta đã thảo luận trước đây, một phép biến đổi có thể làm cho mối quan hệ trở nên tuyến tính, và các phương pháp hồi quy thông thường sau đó có thể được sử dụng trên dữ liệu đã biến đổi. Một khả năng khác, đặc biệt đối với một đường cong, là khớp một đường thẳng vào một phần của đường cong và một đường thẳng thứ hai vào một phần khác của đường cong, một quy trình được gọi là hồi quy tuyến tính từng đoạn. Trong tình huống này, một phương trình hồi quy được sử dụng với tất cả các giá trị X nhỏ hơn một giá trị cho trước, và phương trình thứ hai được sử dụng với tất cả các giá trị X lớn hơn giá trị cho trước. Một chiến lược thứ ba, cũng hữu ích cho các đường cong, là thực hiện hồi quy đa thức; kỹ thuật này được thảo luận trong Chương 10. Cuối cùng, các cách tiếp cận phức tạp hơn được gọi là hồi quy phi tuyến có thể được sử dụng (Snedecor và Cochran, 1989).

Hồi quy về Giá trị Trung bình

Hiện tượng được gọi là hồi quy về giá trị trung bình thường xảy ra trong nghiên cứu ứng dụng và có thể không được nhận ra. Một minh họa tốt về hồi quy về giá trị trung bình đã xảy ra trong nghiên cứu MRFIT (Multiple Risk Factor Intervention Trial Research Group; Gotto, 1997), được thiết kế để đánh giá tác động của chế độ ăn và tập thể dục đối với huyết áp ở nam giới bị tăng huyết áp nhẹ. Để đủ điều kiện tham gia nghiên cứu, nam giới phải có huyết áp tâm trương $\geq 90$ mmHg. Các đối tượng đủ điều kiện sau đó được phân vào nhánh điều trị của nghiên cứu, bao gồm các chương trình khuyến khích chế độ ăn và tập thể dục phù hợp, hoặc nhánh đối chứng, bao gồm chăm sóc thông thường.

Để minh họa khái niệm hồi quy về giá trị trung bình, chúng ta xem xét dữ liệu giả định trong Bảng 8-6 về huyết áp tâm trương ở 12 người đàn ông. Nếu những người đàn ông này đang được sàng lọc cho nghiên cứu MRFIT, chỉ có các đối tượng từ 7 đến 12 sẽ được chấp nhận; các đối tượng từ 1 đến 6 sẽ không đủ điều kiện vì huyết áp tâm trương ban đầu của họ $< 90$ mmHg. Giả sử tất cả các đối tượng được đo huyết áp lại một thời gian sau đó. Vì huyết áp của một người thay đổi đáng kể từ lần đọc này sang lần đọc khác, khoảng một nửa số người đàn ông dự kiến sẽ có huyết áp cao hơn và khoảng một nửa sẽ có huyết áp thấp hơn, do sự biến thiên ngẫu nhiên. Hồi quy về giá trị trung bình cho chúng ta biết rằng những người đàn ông có huyết áp thấp hơn trong lần đọc đầu tiên có nhiều khả năng có huyết áp cao hơn trong lần đọc thứ hai. Tương tự, những người đàn ông có huyết áp tâm trương $\geq 90$ trong lần đọc đầu tiên có nhiều khả năng có huyết áp thấp hơn trong lần đọc thứ hai. Nếu toàn bộ mẫu đàn ông được đo lại, sự tăng và giảm có xu hướng triệt tiêu lẫn nhau. Tuy nhiên, nếu chỉ một tập hợp con của các đối tượng được kiểm tra lại, ví dụ, những người đàn ông có huyết áp tâm trương ban đầu $> 90$ , huyết áp sẽ có vẻ như đã giảm, trong khi thực tế thì không.

Hồi quy về giá trị trung bình có thể dẫn đến việc một phương pháp điều trị hoặc thủ thuật có vẻ có giá trị trong khi thực tế không có tác dụng gì; việc sử dụng một nhóm chứng giúp phòng tránh tác động này. Các nhà điều tra trong nghiên cứu MRFIT đã nhận thức được vấn đề hồi quy về giá trị trung bình và đã thảo luận về các biện pháp phòng ngừa mà họ đã thực hiện để giảm thiểu tác động của nó.

Bảng 8-6. Dữ liệu giả định về huyết áp tâm trương để minh họa hồi quy về giá trị trung bình.

Đối tượng	Ban đầu	Lặp lại
1	78	80
2	80	81
3	82	82
4	84	86
5	86	85
6	88	90
7	90	88
8	92	91
9	94	95
10	96	95
11	98	97
12	100	98

Các Lỗi Thường gặp trong Hồi quy

Một lỗi trong phân tích hồi quy xảy ra khi nhiều quan sát trên cùng một đối tượng được coi như là chúng độc lập. Ví dụ, hãy xem xét mười bệnh nhân có cân nặng và số đo nếp gấp da được ghi lại trước khi bắt đầu một chế độ ăn ít calo. Chúng ta có thể hợp lý kỳ vọng một mối quan hệ dương vừa phải giữa cân nặng và độ dày nếp gấp da. Bây giờ giả sử rằng mười bệnh nhân đó được cân và đo lại sau 6 tuần ăn kiêng. Nếu tất cả 20 cặp đo cân nặng và nếp gấp da được coi như là chúng độc lập, một số vấn đề sẽ xảy ra. Thứ nhất, cỡ mẫu sẽ có vẻ là 20 thay vì 10, và chúng ta có nhiều khả năng kết luận có ý nghĩa thống kê do công suất tăng lên. Thứ hai, vì mối quan hệ giữa cân nặng và độ dày nếp gấp da ở cùng một người có phần ổn định qua những thay đổi nhỏ về cân nặng, việc sử dụng cả quan sát trước và sau chế độ ăn kiêng có tác dụng tương tự như sử dụng các phép đo lặp lại, và điều này dẫn đến một hệ số tương quan lớn hơn mức cần thiết.

Độ lớn của hệ số tương quan cũng có thể bị tăng lên một cách sai lầm do kết hợp hai nhóm khác nhau. Ví dụ, hãy xem xét mối quan hệ giữa chiều cao và cân nặng. Giả sử chiều cao và cân nặng của mười người đàn ông và mười người phụ nữ được ghi lại, và hệ số tương quan giữa chiều cao và cân nặng được tính cho các mẫu kết hợp. Hình 8-13 minh họa biểu đồ phân tán có thể trông như thế nào và chỉ ra vấn đề phát sinh từ việc kết hợp nam và nữ trong một mẫu. Mối quan hệ giữa chiều cao và cân nặng có vẻ có ý nghĩa hơn trong mẫu kết hợp so với khi được đo riêng ở nam và nữ. Phần lớn ý nghĩa rõ ràng này là do nam giới có xu hướng vừa nặng hơn vừa cao hơn phụ nữ. Các kết luận không phù hợp có thể là kết quả của việc trộn lẫn hai quần thể khác nhau—một lỗi khá phổ biến cần chú ý trong y văn.

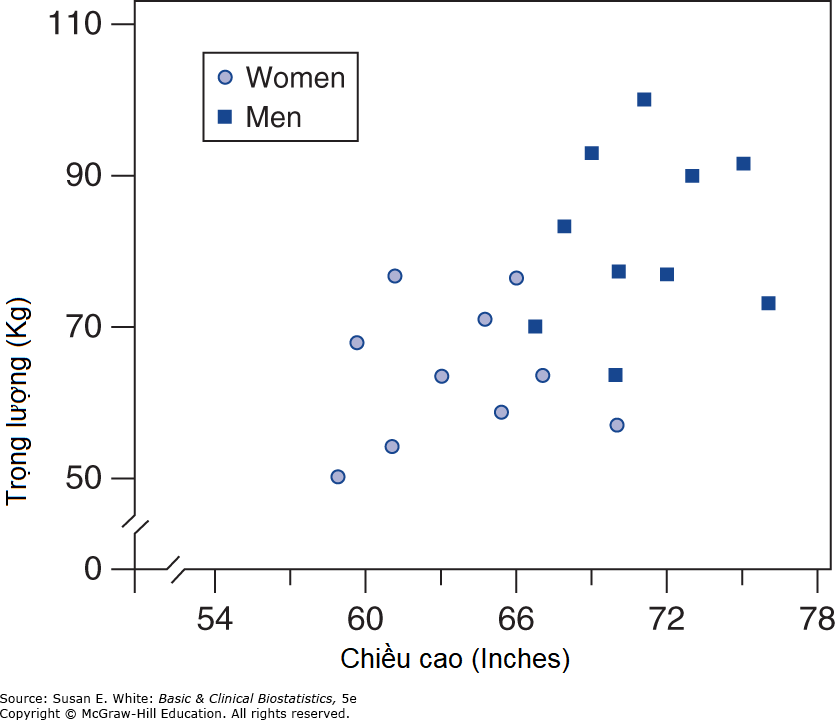
Hình 8-13. Dữ liệu giả định minh họa tương quan giả.

So sánh Tương quan & Hồi quy

Tương quan và hồi quy có một số điểm tương đồng và một số điểm khác biệt. Thứ nhất, tương quan không phụ thuộc vào thang đo, nhưng hồi quy thì có; tức là, tương quan giữa hai đặc tính, chẳng hạn như chiều cao và cân nặng, là như nhau cho dù chiều cao được đo bằng centimet hay inch và cân nặng bằng kilogam hay pound. Tuy nhiên, phương trình hồi quy dự đoán cân nặng từ chiều cao phụ thuộc vào thang đo nào đang được sử dụng; tức là, dự đoán cân nặng đo bằng kilogam từ chiều cao đo bằng centimet cho ra các giá trị khác nhau cho hệ số chặn (a) và độ dốc (b) so với việc dự đoán cân nặng bằng pound từ chiều cao bằng inch.

Một hệ quả quan trọng của việc không phụ thuộc vào thang đo trong tương quan là tương quan giữa X và Y giống như tương quan giữa $Y^{'}$ và Y. Chúng bằng nhau vì bản thân phương trình hồi quy, $Y^{'} = a + b X$ , là một phép tái định tỷ lệ đơn giản của biến X; tức là, mỗi giá trị của X được nhân với một hằng số b và sau đó cộng thêm hằng số a. Thực tế là tương quan giữa các biến ban đầu X và Y bằng với tương quan giữa Y và $Y^{'}$ cung cấp một phương án thay thế hữu ích để kiểm định ý nghĩa của hồi quy, như chúng ta sẽ thấy trong Chương 10. Cuối cùng, độ dốc của đường hồi quy có cùng dấu (+ hoặc -) với hệ số tương quan (xem Bài tập 10). Nếu tương quan bằng không, đường hồi quy nằm ngang với độ dốc bằng không. Do đó, các công thức cho hệ số tương quan và hệ số hồi quy có liên quan chặt chẽ với nhau. Nếu r đã được tính toán, nó có thể được nhân với tỷ số của độ lệch chuẩn của Y và độ lệch chuẩn của X, $S D_{Y} / S D_{X}$ , để có được b (xem Bài tập 9). Do đó,

$b = r \frac{SD_Y}{SD_X}$

Tương tự, nếu hệ số hồi quy đã biết, r có thể được tìm thấy bằng cách: $r = b \frac{SD_X}{SD_Y}$

Hồi quy Đa biến

Phân tích hồi quy đa biến là một sự tổng quát hóa trực tiếp của hồi quy đơn giản cho các ứng dụng trong đó hai hoặc nhiều biến độc lập (giải thích) được sử dụng để dự đoán một kết quả. Ví dụ, trong ví dụ hồi quy đơn giản, chúng ta đã liên hệ BMI và tỷ lệ mỡ cơ thể. Tuy nhiên, chúng ta cũng có thể kiểm soát tuổi của đối tượng. Kết quả từ hai phân tích được đưa ra trong Bảng 8-7. Đầu tiên, hồi quy được thực hiện bằng cách sử dụng BMI để dự đoán tỷ lệ mỡ cơ thể; phương trình kết quả là:

Tỷ lệ mỡ cơ thể dự đoán $= 5.15 + 0.97 \times BM I$

Tiếp theo, hồi quy được lặp lại bằng cách sử dụng cả BMI và tuổi làm biến độc lập. Kết quả là:

Tỷ lệ mỡ cơ thể dự đoán $= 5.13 + 0.96 \times BM I + 0.01 \times T u ổ i$

Như bạn có thể thấy, việc bổ sung biến tuổi có ảnh hưởng tương đối nhỏ; thực tế, giá trị P cho tuổi là 0.91, cho thấy tuổi không liên quan có ý nghĩa với tỷ lệ mỡ cơ thể trong nhóm đối tượng bình thường này.

Thêm một điểm nữa, lưu ý rằng $R^{2}$ (gọi là R-bình phương) là 0.177 cho cả hai phương trình hồi quy trong Bảng 8-7. $R^{2}$ được diễn giải theo cách tương tự như hệ số xác định $r^{2}$ đã được thảo luận trong phần “Diễn giải Độ lớn của r.” Chủ đề này, cùng với hồi quy đa biến và các phương pháp thống kê khác dựa trên hồi quy, sẽ được thảo luận chi tiết trong Chương 10.

Bảng 8-7. Phương trình hồi quy cho tỷ lệ mỡ cơ thể đối với các đối tượng bình thường: BMI so với BMI và tuổi làm biến dự đoán.

Biến độc lập	Hệ số hồi quy	Sai số chuẩn	Giá trị t (Ho: B=0)	Mức xác suất	Quyết định (5%)
Hệ số chặn	5.1539	4.8438	1.064	0.29	Không bác bỏ $H_{0}$
BMI	0.9742	0.2010	4.847	<0.0001	Bác bỏ $H_{0}$
$R^{2}$	0.177

Biến độc lập	Hệ số hồi quy	Sai số chuẩn	Giá trị t (Ho: B=0)	Mức xác suất	Quyết định (5%)
Hệ số chặn	5.13122	0.461	1.064	0.294	Không bác bỏ $H_{0}$
Tuổi	0.01020	0.08602	0.119	0.906	Không bác bỏ $H_{0}$
BMI	0.96420	0.21880	4.407	<0.0001	Bác bỏ $H_{0}$
$R^{2}$	0.177
BMI, chỉ số khối cơ thể.
Dữ liệu từ Neidert LE, Wainright KS, Zheng C, và cộng sự: Plasma dipeptidyl peptidase IV activity and measures of body composition in apparently healthy people, Heliyon. 2016 Apr 18;2(4):e00097.

CỠ MẪU CHO TƯƠNG QUAN & HỒI QUY

Như với các quy trình thống kê khác, điều quan trọng là phải có đủ số lượng đối tượng trong bất kỳ nghiên cứu nào liên quan đến tương quan hoặc hồi quy. Các công thức phức tạp được yêu cầu để ước tính cỡ mẫu cho các quy trình này, nhưng may mắn là chúng ta có thể sử dụng các chương trình công suất thống kê để thực hiện các tính toán.

Giả sử Neidert và cộng sự (2016) muốn biết cỡ mẫu cần thiết để xác định xem tương quan giữa BMI và tỷ lệ mỡ cơ thể có lớn hơn 0.3 với công suất 80% hay không? Chúng tôi đã sử dụng chương trình G*Power để minh họa cỡ mẫu cần thiết trong tình huống này; kết quả được đưa ra trong Hình 8-15. Một mẫu gồm 326 bệnh nhân sẽ là cần thiết. Chúng ta có thể đã sử dụng giả thuyết không là 0.25 thay vì 0.3. Bạn có nghĩ rằng cỡ mẫu sẽ giống nhau không? Hãy thử và xem.

Để minh họa phân tích công suất cho hồi quy, hãy xem xét phương trình hồi quy để dự đoán tỷ lệ mỡ cơ thể từ BMI (Neidert và cộng sự, 2016). Hãy nhớ lại rằng chúng ta đã tìm thấy rằng khoảng tin cậy 95% cho hệ số hồi quy là từ 0.57 đến 1.37 trong toàn bộ mẫu 111 đối tượng. Giả sử Neidert và cộng sự muốn biết cần bao nhiêu đối tượng cho hồi quy. Chương trình công suất GPower tìm cỡ mẫu bằng cách ước tính số lượng cần thiết để có được một giá trị cho trước cho $R^{2}$ (hoặc $r^{2}$ khi chỉ sử dụng một biến độc lập) và độ lệch chuẩn của phần dư. Chúng tôi giả định họ muốn tương quan giữa độ nhạy insulin thực tế và độ nhạy dự đoán ít nhất là 0.50, tạo ra một $r^{2}$ là 0.25 và sử dụng giá trị thực tế của độ lệch chuẩn của phần dư ( $S_{Y . X} = 7.98$ ). Thiết lập và kết quả từ chương trình GPower được đưa ra trong Hình 8-14 và 8-15. Từ Hình 8-15, chúng ta thấy rằng cần có một cỡ mẫu khoảng 21 trong mỗi nhóm mà phương trình hồi quy sẽ được xác định.

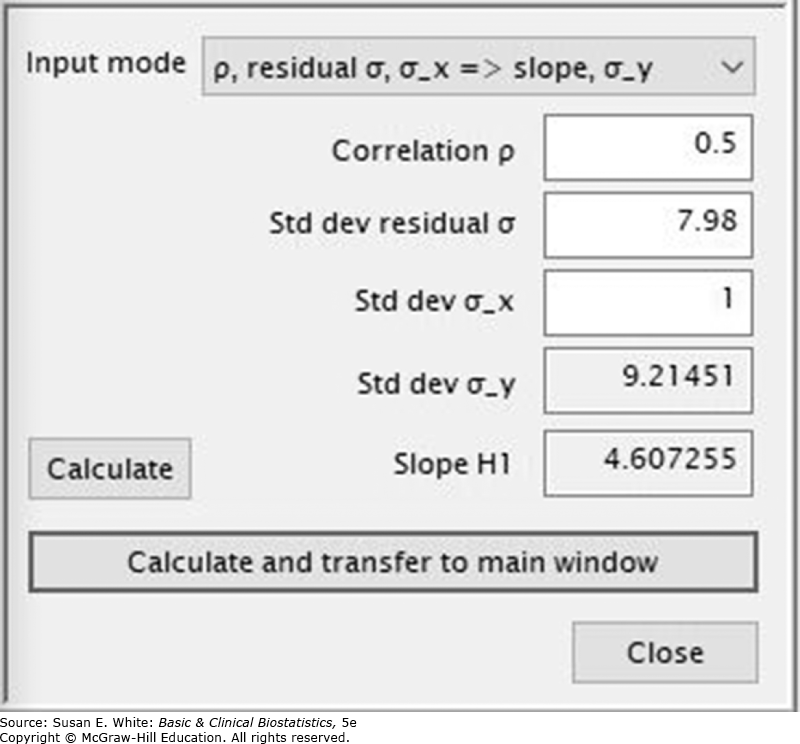Hình 8-14. Dữ liệu đầu vào cho kết quả GPower trong Hình 8-15. (Dữ liệu từ Neidert LE, Wainright KS, Zheng C, và cộng sự: Plasma dipeptidyl peptidase IV activity and measures of body composition in apparently healthy people, Heliyon. 2016 Apr 18;2(4):e00097.)*

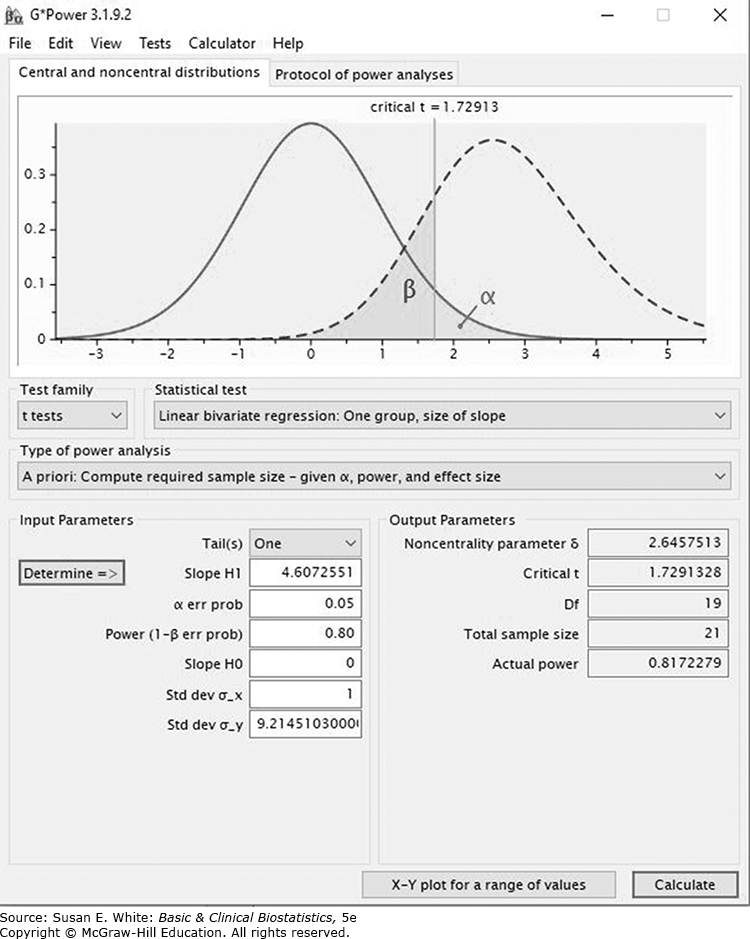
Hình 8-15. Minh họa thiết lập để sử dụng chương trình cỡ mẫu GPower cho hồi quy đa biến sử dụng dữ liệu về tỷ lệ mỡ cơ thể. (Dữ liệu từ Neidert LE, Wainright KS, Zheng C, và cộng sự: Plasma dipeptidyl peptidase IV activity and measures of body composition in apparently healthy people, Heliyon. 2016 Apr 18;2(4):e00097.)*

TÓM TẮT

Hai Vấn đề tình huống đã được sử dụng trong chương này để minh họa ứng dụng của tương quan và hồi quy trong các nghiên cứu y học. Các phát hiện từ nghiên cứu được mô tả trong Vấn đề tình huống 1 chứng minh mối quan hệ giữa BMI và tỷ lệ mỡ cơ thể, một tương quan bằng 0.42. Một số yếu tố khác ngoài BMI đã ảnh hưởng đến mối quan hệ.

Trong Vấn đề tình huống 2, Pereira và cộng sự (2015) đã đánh giá bốn thiết bị đo đường huyết tại giường được quảng cáo là thiết bị chính xác để đo đường huyết. Chúng tôi đã kiểm tra mối quan hệ giữa các thiết bị này và phương pháp tiêu chuẩn sử dụng xét nghiệm động mạch. Các tương quan quan sát được khá cao, dao động từ 0.57 đến 0.87. Chúng tôi đã so sánh hai hệ số tương quan này và kết luận rằng có sự khác biệt thống kê giữa chúng.

Dữ liệu từ Neidert và cộng sự (2016) cũng được sử dụng để minh họa hồi quy, cụ thể là mối quan hệ giữa tỷ lệ mỡ cơ thể và BMI đối với nam và nữ bình thường. Chúng tôi đã tìm thấy các đường hồi quy riêng biệt cho nam và nữ và quan sát thấy rằng các mối quan hệ giữa tỷ lệ mỡ cơ thể và BMI là khác nhau trong hai nhóm đối tượng này.

Các lưu đồ trong Phụ lục C tóm tắt các phương pháp đo lường một mối liên hệ giữa hai đặc tính được đo trên cùng một đối tượng. Lưu đồ C-4 chỉ ra cách các phương pháp phụ thuộc vào thang đo của các biến, và lưu đồ C-5 cho thấy các phương pháp áp dụng để kiểm định sự khác biệt trong các tương quan và trong các đường hồi quy.

BÀI TẬP THỰC HÀNH

a. Thực hiện kiểm định chi-bình phương về ý nghĩa của mối quan hệ giữa việc sử dụng benzodiazepine và sự phát triển sau đó của bệnh Alzheimer bằng cách sử dụng dữ liệu trong Chương 3, Bảng 3-19. b. Xác định giới hạn tin cậy 95% cho nguy cơ tương đối của bệnh Alzheimer ở những đối tượng có liều benzodiazepine hàng ngày bằng cách sử dụng dữ liệu từ Bảng 3-19. Kết luận của bạn là gì?
Tính toán tương quan giữa BMI và tỷ lệ mỡ cơ thể cho toàn bộ mẫu 71 phụ nữ từ Neidert và cộng sự (2016), sử dụng kết quả trong phần “Tính toán Phương trình Hồi quy” cho b. Độ lệch chuẩn của BMI là 3.80 và của tỷ lệ mỡ cơ thể là 6.54.
Helmrich và cộng sự (1987) đã tiến hành một nghiên cứu để đánh giá nguy cơ huyết khối tĩnh mạch sâu và thuyên tắc phổi liên quan đến việc sử dụng thuốc tránh thai đường uống. Họ đặc biệt quan tâm đến nguy cơ liên quan đến liều thấp ( $< 50 μg$ estrogen) và giới hạn nghiên cứu của họ ở phụ nữ dưới 50 tuổi. Họ đã sử dụng các bảng câu hỏi tiêu chuẩn cho những phụ nữ nhập viện vì huyết khối tĩnh mạch sâu hoặc thuyên tắc phổi cũng như cho một nhóm đối chứng gồm những phụ nữ nhập viện vì chấn thương và nhiễm trùng đường hô hấp trên để xác định tiền sử và việc sử dụng thuốc tránh thai đường uống hiện tại của họ. Hai mươi trong số 61 ca bệnh và 121 trong số 1.278 người trong nhóm chứng đã sử dụng thuốc tránh thai đường uống trong tháng trước. a. Thiết kế nghiên cứu nào đã được sử dụng trong nghiên cứu này? b. Tìm giới hạn tin cậy 95% cho tỷ số chênh cho dữ liệu này. c. Các tác giả đã báo cáo một tỷ số chênh đã điều chỉnh theo tuổi là 8.1 với giới hạn tin cậy 95% là 3.7 và 18. Hãy diễn giải những kết quả này.
Vấn đề tình huống 2 trong Chương 3 của Bos-Touwen và cộng sự (2015) đã đo lường điểm số kích hoạt của bệnh nhân, các biến nhân khẩu học và tâm lý xã hội. Sử dụng dữ liệu từ nghiên cứu này và chọn hoặc lọc những đối tượng có giới tính = 1 (nam) và bệnh = 2 (COPD); 184 đối tượng sẽ còn lại cho phân tích. a. Tính toán tương quan giữa điểm nhận thức về bệnh tật (IPQ_Total_score) và điểm SF-12 (SF12_total_score) cho nam giới bị COPD. b. Tạo một khoảng tin cậy 95% cho tương quan này.
Các biểu đồ trong Hình 8-16 được tạo trong Excel bằng cách sử dụng dữ liệu từ Neidert và cộng sự (2016). a. Biểu đồ nào thể hiện mối quan hệ mạnh nhất với tuổi? b. Biến nào sẽ được dự đoán tốt nhất từ tuổi của bệnh nhân?
Giải thích tại sao giá trị trung bình của các giá trị dự đoán, $Y^{'}$ , bằng $Y$ .
Phát triển một lập luận trực quan để giải thích tại sao dấu của hệ số tương quan và dấu của độ dốc của đường hồi quy là giống nhau.
Bài tập nhóm. Nghiên cứu MRFIT (Multiple Risk Factor Intervention Trial Research Group, 1982), đã được gọi là một thử nghiệm mang tính bước ngoặt; đó là thử nghiệm lâm sàng quy mô lớn đầu tiên, và hiếm có một nghiên cứu nào theo dõi hơn 300.000 người đàn ông đã được sàng lọc cho thử nghiệm trong nhiều năm. Tạp chí của Hiệp hội Y khoa Hoa Kỳ đã tái bản bài báo này vào năm 1997. Ngoài ra, tạp chí đã đăng một bài bình luận trong phần Viễn cảnh Landmark của Gotto (1997). Hãy tìm một bản sao của cả hai bài báo.

a. Thiết kế nghiên cứu nào đã được sử dụng trong nghiên cứu?

b. Thảo luận về các tiêu chí đủ điều kiện. Các tiêu chí này có còn phù hợp ngày nay không?

c. Các nhánh điều trị là gì? Các phương pháp điều trị này có còn phù hợp ngày nay không?

d. Các phương pháp thống kê nào đã được sử dụng? Chúng có phù hợp không? Một phương pháp, phương pháp giới hạn sản phẩm Kaplan-Meier, được thảo luận trong Chương 9.

e. Tham khảo Hình 1 trong nghiên cứu gốc. Các đường trong hình chỉ ra điều gì?

f. Kiểm tra phân phối các ca tử vong được đưa ra trong Bảng 4 của bài báo. Phương pháp thống kê nào phù hợp để phân tích các kết quả này?

g. Bài viết viễn cảnh của Gotto thảo luận về vấn đề công suất trong nghiên cứu MRFIT. Công suất của nghiên cứu đã bị ảnh hưởng như thế nào bởi các giả định ban đầu được đưa ra trong thiết kế nghiên cứu?

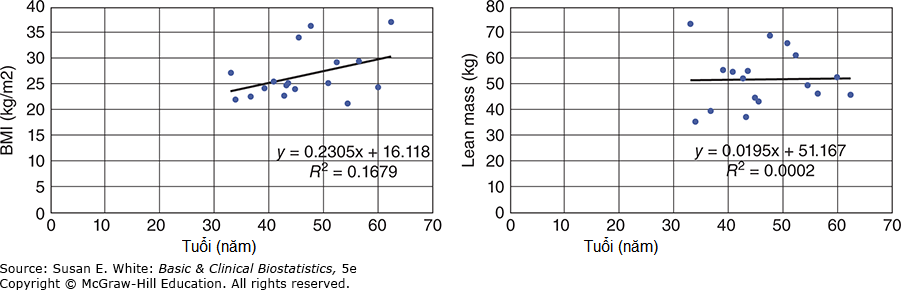
Hình 8-16. Biểu đồ phân tán và đường hồi quy cho mối quan hệ giữa tuổi và BMI; tuổi và Khối lượng nạc. (Dữ liệu từ Neidert LE, Wainright KS, Zheng C, và cộng sự: Plasma dipeptidyl peptidase IV activity and measures of body composition in apparently healthy people, Heliyon. 2016 Apr 18;2(4):e00097.)

Bảng Chú Giải Thuật Ngữ Thống kê Anh-Việt (Chương 8)

STT	Thuật ngữ tiếng Anh	Phiên âm	Nghĩa Tiếng Việt
1	Relationships	/rɪˈleɪʃənˌʃɪps/	Mối quan hệ
2	Variables	/ˈvɛəriəbəlz/	Biến số
3	Correlation	/ˌkɔːrəˈleɪʃn/	Tương quan
4	Regression	/rɪˈɡrɛʃn/	Hồi quy
5	Statistical methods	/stəˈtɪstɪkəl ˈmɛθədz/	Các phương pháp thống kê
6	Linear relationship	/ˈlɪniər rɪˈleɪʃənˌʃɪp/	Mối quan hệ tuyến tính
7	Numerical variables	/nuˈmɛrɪkəl ˈvɛəriəbəlz/	Biến số định lượng
8	Subjects	/ˈsʌbdʒɪkts/	Đối tượng (nghiên cứu)
9	Predicts	/prɪˈdɪkts/	Dự đoán
10	Outcome	/ˈaʊtˌkʌm/	Kết quả, kết cục
11	Correlation coefficients	/ˌkɔːrəˈleɪʃn ˌkoʊɪˈfɪʃənts/	Hệ số tương quan
12	Perfect relationship	/ˈpɜːrfɪkt rɪˈleɪʃənˌʃɪp/	Mối quan hệ hoàn hảo
13	Scatterplots	/ˈskætərˌplɑːts/	Biểu đồ phân tán
14	Visual display	/ˈvɪʒuəl dɪˈspleɪ/	Trình bày trực quan
15	Extreme values	/ɪkˈstriːm ˈvæljuːz/	Giá trị ngoại lai, giá trị cực biên
16	Coefficient of determination	/ˌkoʊɪˈfɪʃənt əv dɪˌtɜːrmɪˈneɪʃn/	Hệ số xác định
17	Squared correlation	/skwɛərd ˌkɔːrəˈleɪʃn/	Tương quan bình phương
18	Preferred statistic	/prɪˈfɜːrd stəˈtɪstɪk/	Thống kê ưu tiên
19	Strength	/strɛŋkθ/	Độ mạnh (của mối quan hệ)
20	t test	/tiː tɛst/	Kiểm định t
21	Hypothesis	/haɪˈpɑːθəsɪs/	Giả thuyết
22	Population correlation	/ˌpɑːpjuˈleɪʃn ˌkɔːrəˈleɪʃn/	Tương quan quần thể
23	Fisher z transformation	/ˈfɪʃər ziː ˌtrænsfərˈmeɪʃn/	Phép biến đổi z của Fisher
24	Confidence intervals	/ˈkɑːnfɪdəns ˈɪntərvəlz/	Khoảng tin cậy
25	Skewed	/skjuːd/	Lệch, không đối xứng
26	Spearman rho	/ˈspɪərmən roʊ/	Hệ số rho của Spearman
27	Nonparametric correlation	/ˌnɑːnpærəˈmɛtrɪk ˌkɔːrəˈleɪʃn/	Tương quan phi tham số
28	Linear regression	/ˈlɪniər rɪˈɡrɛʃn/	Hồi quy tuyến tính
29	Straight-line relationships	/streɪt laɪn rɪˈleɪʃənˌʃɪps/	Mối quan hệ đường thẳng
30	Least squares method	/liːst skwɛərz ˈmɛθəd/	Phương pháp bình phương tối thiểu
31	Independent variable	/ˌɪndɪˈpɛndənt ˈvɛəriəbəl/	Biến độc lập
32	Dependent variable	/dɪˈpɛndənt ˈvɛəriəbəl/	Biến phụ thuộc
33	Regression equation	/rɪˈɡrɛʃn ɪˈkweɪʒən/	Phương trình hồi quy
34	Straight line	/streɪt laɪn/	Đường thẳng
35	Standard error of the estimate	/ˈstændərd ˈɛrər əv ðə ˈɛstəmət/	Sai số chuẩn của ước lượng
36	Intercept	/ˈɪntərˌsɛpt/	Hệ số chặn
37	Regression coefficient	/rɪˈɡrɛʃn ˌkoʊɪˈfɪʃənt/	Hệ số hồi quy
38	Slope	/sloʊp/	Độ dốc, hệ số góc
39	Confidence bands	/ˈkɑːnfɪdəns bændz/	Dải tin cậy
40	Regression line	/rɪˈɡrɛʃn laɪn/	Đường hồi quy
41	Mean	/miːn/	Giá trị trung bình
42	Residual	/rɪˈzɪdʒuəl/	Phần dư
43	Predicted outcome	/prɪˈdɪktɪd ˈaʊtˌkʌm/	Kết quả dự đoán
44	Linear regression model	/ˈlɪniər rɪˈɡrɛʃn ˈmɑːdl/	Mô hình hồi quy tuyến tính
45	Regression toward the mean	/rɪˈɡrɛʃn təˈwɔːrd ðə miːn/	Hồi quy về giá trị trung bình
46	Treatment	/ˈtriːtmənt/	Điều trị
47	Procedure	/prəˈsiːdʒər/	Thủ thuật, quy trình
48	Control group	/kənˈtroʊl ɡruːp/	Nhóm chứng
49	Observations	/ˌɑːbzərˈveɪʃənz/	Quan sát
50	Independent	/ˌɪndɪˈpɛndənt/	Độc lập
51	Multiple measurements	/ˈmʌltəpəl ˈmɛʒərmənts/	Đo lường đa điểm, đo lường lặp lại
52	Populations	/ˌpɑːpjuˈleɪʃənz/	Quần thể
53	Multiple regression	/ˈmʌltəpəl rɪˈɡrɛʃn/	Hồi quy đa biến
54	Sample size	/ˈsæmpəl saɪz/	Cỡ mẫu
55	Power analysis	/ˈpaʊər əˈnælɪsɪs/	Phân tích công suất (của kiểm định)
56	Body composition	/ˈbɑːdi ˌkɑːmpəˈzɪʃn/	Thành phần cơ thể
57	Plasma	/ˈplæzmə/	Huyết tương
58	Gynoid fat	/ˈɡaɪnɔɪd fæt/	Mỡ vùng hông đùi
59	BMI (Body Mass Index)	/ˌbiː ɛm ˈaɪ/	Chỉ số khối cơ thể
60	Lean mass	/liːn mæs/	Khối lượng nạc
61	Recruited	/rɪˈkruːtɪd/	Tuyển chọn (đối tượng)
62	Adult mixed-ICU	/əˈdʌlt mɪkst aɪ siː juː/	Đơn vị hồi sức tích cực hỗn hợp người lớn
63	Accuracy	/ˈækjərəsi/	Độ chính xác
64	Blood glucose levels	/blʌd ˈɡluːkoʊs ˈlɛvəlz/	Nồng độ đường huyết
65	Bedside	/ˈbɛdˌsaɪd/	Tại giường bệnh
66	Arterial	/ɑːrˈtɪəriəl/	(Thuộc) động mạch
67	Fingerstick	/ˈfɪŋɡərˌstɪk/	Lấy máu đầu ngón tay
68	Venous	/ˈviːnəs/	(Thuộc) tĩnh mạch
69	Gold standard	/ɡoʊld ˈstændərd/	Tiêu chuẩn vàng
70	Central lab	/ˈsɛntrəl læb/	Phòng xét nghiệm trung tâm
71	Association	/əˌsoʊsiˈeɪʃn/	Sự liên hợp, sự liên quan
72	Statistical procedures	/stəˈtɪstɪkəl prəˈsiːdʒərz/	Các quy trình thống kê
73	Significant	/sɪɡˈnɪfɪkənt/	Có ý nghĩa (thống kê)
74	Probability distributions	/ˌprɑːbəˈbɪləti ˌdɪstrɪˈbjuːʃənz/	Phân phối xác suất
75	Chi-square distribution	/kaɪ skwɛər ˌdɪstrɪˈbjuːʃən/	Phân phối chi-bình phương
76	Dependent variable	/dɪˈpɛndənt ˈvɛəriəbəl/	Biến phụ thuộc
77	Response variable	/rɪˈspɑːns ˈvɛəriəbəl/	Biến đáp ứng
78	Explanatory variable	/ɪkˈsplænəˌtɔːri ˈvɛəriəbəl/	Biến giải thích
79	Technique	/tɛkˈniːk/	Kỹ thuật
80	Analysis	/əˈnælɪsɪs/	Phân tích
81	Assumptions	/əˈsʌmpʃənz/	Giả định
82	Hypothetical	/ˌhaɪpəˈθɛtɪkəl/	Giả định, giả thuyết
83	Plotted points	/ˈplɑːtɪd pɔɪnts/	Các điểm được vẽ
84	Circular	/ˈsɜːrkjələr/	(Hình) tròn
85	Oval	/ˈoʊvəl/	(Hình) bầu dục
86	Nonlinear relationship	/ˌnɑːnˈlɪniər rɪˈleɪʃənˌʃɪp/	Mối quan hệ phi tuyến
87	Nerve fiber	/nɜːrv ˈfaɪbər/	Sợi thần kinh
88	Impulses	/ˈɪmpʌlsɪz/	Xung động (thần kinh)
89	Pearson product moment	/ˈpɪərsən ˈprɑːdʌkt ˈmoʊmənt/	Tích-momen Pearson
90	Graphically	/ˈɡræfɪkli/	Bằng đồ thị, một cách trực quan
91	Y-axis	/waɪ ˈæksɪs/	Trục Y
92	X-axis	/ɛks ˈæksɪs/	Trục X
93	Positive relationship	/ˈpɑːzətɪv rɪˈleɪʃənˌʃɪp/	Mối quan hệ dương, tương quan thuận
94	Statistically significant	/stəˈtɪstɪkli sɪɡˈnɪfɪkənt/	Có ý nghĩa thống kê
95	Statistical program	/stəˈtɪstɪkəl ˈproʊɡræm/	Chương trình thống kê
96	Properties	/ˈprɑːpərtiːz/	Thuộc tính, đặc tính
97	Variation	/ˌvɛəriˈeɪʃn/	Sự biến thiên
98	Venn diagrams	/vɛn ˈdaɪəˌɡræmz/	Biểu đồ Venn
99	Population parameter	/ˌpɑːpjuˈleɪʃn pəˈræmɪtər/	Tham số quần thể
100	Random sample	/ˈrændəm ˈsæmpəl/	Mẫu ngẫu nhiên
101	Sampling distribution	/ˈsæmplɪŋ ˌdɪstrɪˈbjuːʃən/	Phân phối lấy mẫu
102	Ceiling effect	/ˈsiːlɪŋ ɪˈfɛkt/	Hiệu ứng trần
103	Skewed distribution	/skjuːd ˌdɪstrɪˈbjuːʃən/	Phân phối lệch
104	t ratio	/tiː ˈreɪʃioʊ/	Tỷ số t
105	Degrees of freedom	/dɪˈɡriːz əv ˈfriːdəm/	Bậc tự do
106	Null hypothesis	/nʌl haɪˈpɑːθəsɪs/	Giả thuyết không
107	Alternative hypothesis	/ɔːlˈtɜːrnətɪv haɪˈpɑːθəsɪs/	Giả thuyết đối
108	Critical value	/ˈkrɪtɪkəl ˈvæljuː/	Giá trị tới hạn
109	One-tailed test	/wʌn teɪld tɛst/	Kiểm định một phía
110	Standard normal distribution	/ˈstændərd ˈnɔːrməl ˌdɪstrɪˈbjuːʃən/	Phân phối chuẩn tắc
111	Natural logarithm	/ˈnætʃərəl ˈlɔːɡəˌrɪðəm/	Logarit tự nhiên
112	z test	/ziː tɛst/	Kiểm định z
113	Confidence coefficient	/ˈkɑːnfɪdəns ˌkoʊɪˈfɪʃənt/	Hệ số tin cậy
114	Standard error	/ˈstændərd ˈɛrər/	Sai số chuẩn
115	Bivariate normal distribution	/baɪˈvɛəriət ˈnɔːrməl ˌdɪstrɪˈbjuːʃən/	Phân phối chuẩn hai biến
116	Transformed	/trænsˈfɔːrmd/	(Được) biến đổi
117	Rank correlation	/ræŋk ˌkɔːrəˈleɪʃn/	Tương quan hạng
118	Independent groups	/ˌɪndɪˈpɛndənt ɡruːps/	Các nhóm độc lập
119	Dependent correlations	/dɪˈpɛndənt ˌkɔːrəˈleɪʃənz/	Các tương quan phụ thuộc
120	Correlation matrix	/ˌkɔːrəˈleɪʃn ˈmeɪtrɪks/	Ma trận tương quan
121	Venous catheter	/ˈviːnəs ˈkæθɪtər/	Catheter tĩnh mạch
122	Ordinal data	/ˈɔːrdnəl ˈdeɪtə/	Dữ liệu thứ bậc
123	Point-biserial correlation	/pɔɪnt baɪˈsɪəriəl ˌkɔːrəˈleɪʃn/	Tương quan điểm-nhị phân
124	Nominal data	/ˈnɑːmɪnəl ˈdeɪtə/	Dữ liệu danh nghĩa
125	Risk ratio	/rɪsk ˈreɪʃioʊ/	Tỷ số nguy cơ
126	Kappa (κ)	/ˈkæpə/	Hệ số Kappa (κ)
127	Outlying values	/aʊtˈlaɪɪŋ ˈvæljuːz/	Giá trị ngoại lai
128	Normal probability plot	/ˈnɔːrməl ˌprɑːbəˈbɪləti plɑːt/	Biểu đồ xác suất chuẩn
129	Ranks	/ræŋks/	Hạng, thứ hạng
130	Tied values	/taɪd ˈvæljuːz/	Các giá trị bằng nhau (trùng hạng)
131	Population value	/ˌpɑːpjuˈleɪʃn ˈvæljuː/	Giá trị quần thể
132	Odds ratio	/ɑːdz ˈreɪʃioʊ/	Tỷ số chênh
133	Relative risk	/ˈrɛlətɪv rɪsk/	Nguy cơ tương đối
134	Epidemiologists	/ˌɛpɪˌdiːmiˈɑːlədʒɪsts/	Nhà dịch tễ học
135	Benzodiazepine exposure	/ˌbɛnzoʊdaɪˈæzəˌpiːn ɪkˈspoʊʒər/	Phơi nhiễm Benzodiazepine
136	Alzheimer’s disease	/ˈɑːltshaɪmərz dɪˈziːz/	Bệnh Alzheimer
137	Chi-square test	/kaɪ skwɛər tɛst/	Kiểm định chi-bình phương
138	Antilogarithm	/ˌæntiˈlɔːɡəˌrɪðəm/	Đối logarit
139	Exponential function	/ˌɛkspəˈnɛnʃəl ˈfʌŋkʃən/	Hàm mũ
140	2×2 table	/tuː baɪ tuː ˈteɪbəl/	Bảng 2×2
141	Flu vaccine	/fluː vækˈsiːn/	Vắc-xin cúm
142	Flu diagnosis	/fluː ˌdaɪəɡˈnoʊsɪs/	Chẩn đoán cúm
143	Continuity correction	/ˌkɑːntəˈnuːəti kəˈrɛkʃən/	Hiệu chỉnh liên tục
144	Simple linear regression	/ˈsɪmpəl ˈlɪniər rɪˈɡrɛʃn/	Hồi quy tuyến tính đơn giản
145	Heredity	/həˈrɛdəti/	Di truyền
146	Filial type	/ˈfɪliəl taɪp/	Kiểu hình con
147	Parental type	/pəˈrɛntl taɪp/	Kiểu hình cha mẹ
148	Ancestral type	/ænˈsɛstrəl taɪp/	Kiểu hình tổ tiên
149	Co-relation	/koʊ rɪˈleɪʃn/	Đồng tương quan
150	Prediction equation	/prɪˈdɪkʃən ɪˈkweɪʒən/	Phương trình dự đoán
151	Error term	/ˈɛrər tɜːrm/	Thành phần sai số
152	Predicted value	/prɪˈdɪktɪd ˈvæljuː/	Giá trị dự đoán
153	Minimized	/ˈmɪnɪˌmaɪzd/	(Được) tối thiểu hóa
154	Differential calculus	/ˌdɪfəˈrɛnʃəl ˈkælkjələs/	Phép tính vi phân
155	Partial derivatives	/ˈpɑːrʃəl dɪˈrɪvətɪvz/	Đạo hàm riêng
156	Insulin sensitivity	/ˈɪnsəlɪn ˌsɛnsɪˈtɪvəti/	Độ nhạy insulin
157	Homogeneity	/ˌhoʊmədʒəˈniːəti/	Tính đồng nhất
158	Homoscedasticity	/ˌhoʊmoʊskɛdæˈstɪsəti/	Phương sai đồng nhất
159	Homogeneous variances	/hoʊˈmɑːdʒənəs ˈvɛəriənsɪz/	Các phương sai đồng nhất
160	Repeated measurements	/rɪˈpiːtɪd ˈmɛʒərmənts/	Đo lường lặp lại
161	Robust procedure	/roʊˈbʌst prəˈsiːdʒər/	Quy trình mạnh
162	Clinical trials	/ˈklɪnɪkəl ˈtraɪəlz/	Thử nghiệm lâm sàng
163	Observational studies	/ˌɑːbzərˈveɪʃənl ˈstʌdiːz/	Nghiên cứu quan sát
164	Statistician	/ˌstætɪˈstɪʃn/	Nhà thống kê
165	Denominator	/dɪˈnɑːmɪˌneɪtər/	Mẫu số
166	Spreadsheet	/ˈsprɛdˌʃiːt/	Bảng tính
167	P values	/piː ˈvæljuːz/	Giá trị p
168	Participants	/pɑːrˈtɪsəpənts/	Người tham gia
169	Fitness regimen	/ˈfɪtnəs ˈrɛdʒəmən/	Chế độ luyện tập
170	Economists	/ɪˈkɑːnəmɪsts/	Nhà kinh tế học
171	Concave	/kɑːnˈkeɪv/	Lõm
172	Coincident	/koʊˈɪnsɪdənt/	Trùng nhau
173	Pooling observations	/ˈpuːlɪŋ ˌɑːbzərˈveɪʃənz/	Gộp các quan sát
174	Curvilinear relationship	/ˌkɜːrvɪˈlɪniər rɪˈleɪʃənˌʃɪp/	Mối quan hệ cong
175	Random scatter	/ˈrændəm ˈskætər/	Phân tán ngẫu nhiên
176	Piecewise linear regression	/ˈpiːsˌwaɪz ˈlɪniər rɪˈɡrɛʃn/	Hồi quy tuyến tính từng đoạn
177	Polynomial regression	/ˌpɑːlɪˈnoʊmiəl rɪˈɡrɛʃn/	Hồi quy đa thức
178	Nonlinear regression	/ˌnɑːnˈlɪniər rɪˈɡrɛʃn/	Hồi quy phi tuyến
179	Mild hypertension	/maɪld ˌhaɪpərˈtɛnʃn/	Tăng huyết áp nhẹ
180	Diastolic blood pressure	/ˌdaɪəˈstɑːlɪk blʌd ˈprɛʃər/	Huyết áp tâm trương
181	Treatment arm	/ˈtriːtmənt ɑːrm/	Nhánh điều trị
182	Control arm	/kənˈtroʊl ɑːrm/	Nhánh chứng
183	Baseline	/ˈbeɪsˌlaɪn/	(Giá trị) ban đầu, nền
184	Random variation	/ˈrændəm ˌvɛəriˈeɪʃn/	Biến thiên ngẫu nhiên
185	Skinfold measurements	/ˈskɪnˌfoʊld ˈmɛʒərmənts/	Đo nếp gấp da
186	Low-calorie diet	/loʊ ˈkæləri ˈdaɪət/	Chế độ ăn ít calo
187	Duplicate measures	/ˈduːplɪkət ˈmɛʒərz/	Các phép đo trùng lặp
188	Spurious correlation	/ˈspjʊəriəs ˌkɔːrəˈleɪʃn/	Tương quan giả
189	Scale-independent	/skeɪl ˌɪndɪˈpɛndənt/	Không phụ thuộc thang đo
190	Centimeters	/ˈsɛntəˌmiːtərz/	Centimet
191	Inches	/ˈɪntʃɪz/	Inch
192	Kilograms	/ˈkɪləˌɡræmz/	Kilogam
193	Pounds	/paʊndz/	Pound
194	Rescaling	/riːˈskeɪlɪŋ/	Tái định tỷ lệ
195	Deep vein thrombosis	/diːp veɪn θrɑːmˈboʊsɪs/	Huyết khối tĩnh mạch sâu
196	Pulmonary embolism	/ˈpʊlməˌnɛri ˈɛmbəˌlɪzəm/	Thuyên tắc phổi
197	Oral contraceptives	/ˈɔːrəl ˌkɑːntrəˈsɛptɪvz/	Thuốc tránh thai đường uống
198	Questionnaires	/ˌkwɛstʃəˈnɛərz/	Bảng câu hỏi
199	Trauma	/ˈtrɔːmə/	Chấn thương
200	Upper respiratory infections	/ˈʌpər ˈrɛspərəˌtɔːri ɪnˈfɛkʃənz/	Nhiễm trùng đường hô hấp trên

Thống kê Sinh học Cơ bản và Lâm sàng, Ấn bản thứ 5. Chương 8: Các Câu Hỏi Nghiên Cứu Về Mối Quan Hệ Giữa Các Biến Số