Thống kê Sinh học Cơ bản và Lâm sàng, Ấn bản thứ 5 – Basic & Clinical Biostatistics, 5e
Tác giả: Susan White – Nhà xuất bản McGraw-Hill Medical – Biên dịch: Ths.Bs. Lê Đình Sáng
Chương 9: Phân tích các Câu hỏi Nghiên cứu về Sự sống còn
Analyzing Research Questions About Survival
NHỮNG KHÁI NIỆM CHÍNH
|
VẤN ĐỀ MỞ ĐẦU
Ung thư đại trực tràng di căn có thể được điều trị bằng regorafenib đơn độc hoặc regorafenib kết hợp với hóa trị. Lin và cộng sự (2018) đã nghiên cứu các đường cong sống còn của bệnh nhân theo mỗi phương pháp điều trị. Họ đã phân tích dữ liệu từ 61 bệnh nhân hoàn thành nghiên cứu: 34 người dùng regorafenib kết hợp với hóa trị và 27 người chỉ dùng regorafenib đơn độc.
MỤC ĐÍCH CỦA CHƯƠNG
Nhiều nghiên cứu trong y học được thiết kế để xác định xem một loại thuốc mới, một phương pháp điều trị mới, hoặc một quy trình mới có hoạt động tốt hơn so với phương pháp hiện đang được sử dụng hay không. Mặc dù các thước đo về hiệu quả ngắn hạn được quan tâm trong nỗ lực cung cấp dịch vụ chăm sóc sức khỏe hiệu quả hơn, các kết cục dài hạn, bao gồm tỷ lệ tử vong và các bệnh tật chính, cũng rất quan trọng. Thông thường, các nghiên cứu tập trung vào việc so sánh thời gian sống còn của hai hoặc nhiều nhóm bệnh nhân.
Các phương pháp phân tích dữ liệu đã được thảo luận trong các chương trước không phù hợp để đo lường thời gian sống còn vì hai lý do.
- Thứ nhất, các nhà điều tra thường phải phân tích dữ liệu trước khi tất cả bệnh nhân qua đời; nếu không, có thể mất nhiều năm trước khi họ biết được phương pháp điều trị nào tốt hơn. Khi phân tích sự sống còn được thực hiện trong khi một số bệnh nhân trong nghiên cứu vẫn còn sống, các quan sát trên những bệnh nhân này được gọi là quan sát bị kiểm duyệt (censored observations), vì chúng ta không biết những bệnh nhân này sẽ sống được bao lâu nữa. Hình 9-1 minh họa một tình huống trong đó các quan sát trên bệnh nhân B và E bị kiểm duyệt.
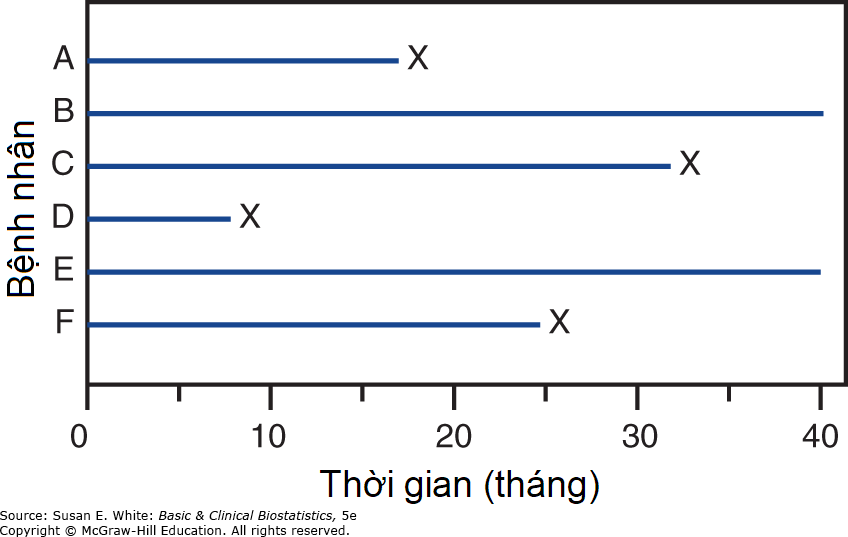
Hình 9-1. Ví dụ về các quan sát bị kiểm duyệt (X có nghĩa là bệnh nhân đã qua đời).
- Lý do thứ hai cần các phương pháp đặc biệt để phân tích dữ liệu sống còn là bệnh nhân thường không bắt đầu điều trị hoặc tham gia nghiên cứu cùng một lúc, như trong Hình 9-1. Khi thời điểm tham gia của bệnh nhân không đồng thời và một số bệnh nhân vẫn còn trong nghiên cứu khi phân tích được thực hiện, dữ liệu được gọi là bị kiểm duyệt lũy tiến (progressively censored). Hình 9-2 cho thấy kết quả của một nghiên cứu với các quan sát bị kiểm duyệt lũy tiến. Nghiên cứu bắt đầu tại thời điểm 0 tháng với bệnh nhân A; sau đó, bệnh nhân B tham gia nghiên cứu tại thời điểm 7 tháng; bệnh nhân C tham gia tại thời điểm 8 tháng; và cứ thế tiếp tục. Bệnh nhân B và E vẫn còn sống tại thời điểm dữ liệu được phân tích là 40 tháng.
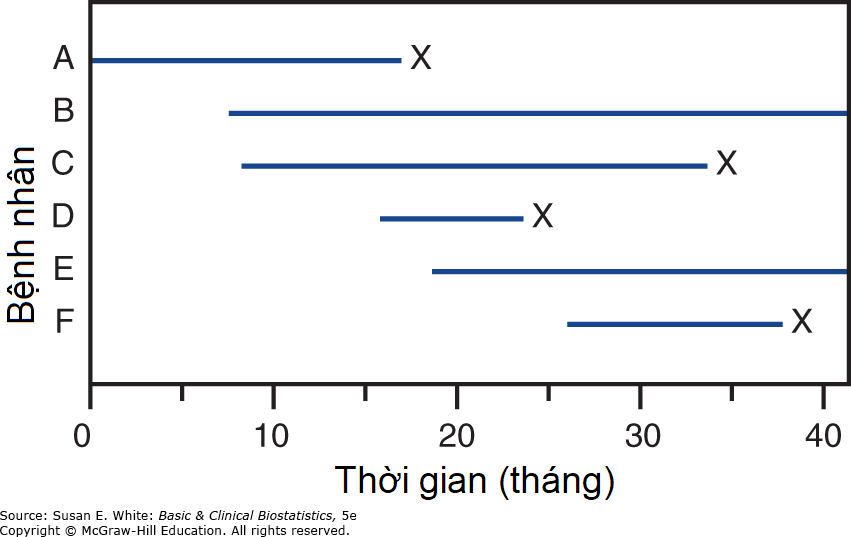
Hình 9-2. Ví dụ về các quan sát bị kiểm duyệt lũy tiến (X có nghĩa là bệnh nhân đã qua đời).
Phân tích thời gian sống còn đôi khi được gọi là phân tích tính toán bảo hiểm (actuarial), hoặc bảng sống (life table). Về mặt lịch sử, nhà thiên văn học Edmund Halley (nổi tiếng với Sao chổi Halley) đã lần đầu tiên sử dụng bảng sống vào thế kỷ XVII để mô tả thời gian sống còn của cư dân một thị trấn. Kể từ đó, các phương pháp này đã được sử dụng theo nhiều cách khác nhau. Các công ty bảo hiểm nhân thọ sử dụng chúng để xác định tuổi thọ dự kiến của các cá nhân, và thông tin này sau đó được sử dụng để thiết lập các biểu phí bảo hiểm. Các công ty bảo hiểm thường sử dụng dữ liệu cắt ngang về thời gian sống dự kiến của những người ở các nhóm tuổi khác nhau để xây dựng một bảng sống hiện tại. Tuy nhiên, trong y học, hầu hết các nghiên cứu về sự sống còn sử dụng bảng sống đoàn hệ (cohort life tables), trong đó cùng một nhóm đối tượng được theo dõi trong một khoảng thời gian nhất định. Dữ liệu cho các bảng sống có thể đến từ các nghiên cứu đoàn hệ (tiến cứu hoặc hồi cứu) hoặc từ các thử nghiệm lâm sàng; đặc điểm chính là cùng một nhóm đối tượng được theo dõi trong một khoảng thời gian đã định.
Trong chương này, chúng ta sẽ xem xét hai phương pháp để xác định đường cong sống còn. Thực ra, mô tả chúng là các phương pháp để kiểm tra các đường cong với dữ liệu bị kiểm duyệt sẽ chính xác hơn, bởi vì nhiều khi kết cục không phải là sự sống còn.
TẠI SAO CẦN CÓ CÁC PHƯƠNG PHÁP CHUYÊN BIỆT ĐỂ PHÂN TÍCH DỮ LIỆU SỐNG CÒN
Trước khi minh họa các phương pháp phân tích dữ liệu sống còn, chúng ta hãy xem xét ngắn gọn tại sao một số phương pháp trực quan lại không hữu ích hoặc không phù hợp. Để minh họa những điểm này, chúng tôi đã chọn một mẫu gồm 28 bệnh nhân đang được điều trị ung thư ruột kết di căn: 14 bệnh nhân dùng regorafenib đơn độc (R) và 14 bệnh nhân dùng regorafenib kết hợp với hóa trị (Bảng 9-1).
Bảng 9-1. Báo cáo dữ liệu trên một mẫu 28 bệnh nhân.
|
Ca |
Giới tính | Tuổi | Điều trị | Số tháng sống không bệnh tiến triển | Số tháng sống còn | Tình trạng sống |
|---|---|---|---|---|---|---|
| 1 | Nữ | 67 | R | 1.61 | 10.28 | 1 |
| 2 | Nam | 81 | R | 2.99 | 5.55 | 1 |
| 3 | Nam | 73 | R | 4.34 | 5.82 | 1 |
| 4 | Nam | 58 | R | 4.07 | 8.90 | 1 |
| 5 | Nữ | 54 | R | 2.53 | 10.41 | 1 |
| 6 | Nam | 43 | R | 2.63 | 10.68 | 1 |
| 8 | Nam | 60 | R | 1.58 | 3.71 | 1 |
| 9 | Nữ | 54 | R | 5.78 | 20.01 | 0 |
| 11 | Nữ | 40 | R | 2.04 | 9.00 | 1 |
| 13 | Nam | 55 | R | 0.92 | 5.09 | 1 |
| 14 | Nam | 48 | R | 0.69 | 10.55 | 1 |
| 15 | Nữ | 57 | R | 2.66 | 12.16 | 0 |
| 16 | Nam | 60 | R | 2.76 | 13.17 | 1 |
| 18 | Nam | 60 | R | 7.82 | 10.55 | 1 |
| 7 | Nữ | 67 | C | 5.06 | 17.71 | 0 |
| 10 | Nữ | 66 | C | 0.92 | 11.30 | 1 |
| 12 | Nam | 75 | C | 2.53 | 9.43 | 1 |
| 17 | Nữ | 67 | C | 6.21 | 14.95 | 0 |
| 19 | Nam | 62 | C | 8.74 | 20.90 | 1 |
| 30 | Nữ | 61 | C | 2.79 | 11.201 | 1 |
| 21 | Nam | 58 | C | 7.59 | 21.19 | 0 |
| 22 | Nam | 80 | C | 1.84 | 4.44 | 1 |
| 23 | Nam | 47 | C | 4.83 | 19.81 | 0 |
| 24 | Nam | 76 | C | 16.59 | 18.56 | 0 |
| 25 | Nam | 56 | C | 2.96 | 10.61 | 1 |
| 26 | Nữ | 59 | C | 2.63 | 4.99 | 1 |
| 27 | Nam | 61 | C | 4.86 | 19.55 | 0 |
| 28 | Nữ | 61 | C | 0.92 | 7.13 | 1 |
| Ghi chú: 1 = Đã mất, 0 = Còn sống. C = Điều trị kết hợp, R = Regorafenib đơn độc. Dữ liệu từ Lin C-Y, và cộng sự (2018). | ||||||
Colton (1974, trang 238-241) đưa ra một trình bày sáng tạo về một số phương pháp đơn giản để phân tích dữ liệu sống còn; các lập luận được trình bày trong phần này được mô phỏng theo thảo luận của ông. Một số phương pháp thoạt nhìn có vẻ phù hợp để phân tích dữ liệu sống còn, nhưng khi xem xét kỹ hơn lại thấy chúng không chính xác.
Giả sử có người đề nghị tính toán thời gian sống trung bình của bệnh nhân ung thư ruột kết di căn. Sử dụng dữ liệu của 28 bệnh nhân trong Bảng 9-1, thời gian sống trung bình của bệnh nhân điều trị kết hợp regorafenib là 13,70 tháng, và của bệnh nhân chỉ dùng regorafenib là 9,70 tháng. Vấn đề là thời gian sống trung bình phụ thuộc vào thời điểm dữ liệu được phân tích; nó sẽ thay đổi theo từng tháng trôi qua cho đến khi tất cả các đối tượng đã qua đời. Do đó, các ước tính thời gian sống trung bình được tính theo cách này chỉ hữu ích khi tất cả các đối tượng đã qua đời hoặc biến cố đang được phân tích đã xảy ra. Tuy nhiên, hầu hết các nhà điều tra đều muốn phân tích dữ liệu của họ trước thời điểm đó.
Ước tính thời gian sống trung vị cũng có thể thực hiện, và nó có thể được tính sau khi chỉ một nửa số đối tượng đã qua đời. Tuy nhiên, một lần nữa, các nhà điều tra thường muốn đánh giá kết quả trước thời điểm đó.
Một khái niệm đôi khi được sử dụng trong dịch tễ học là số ca tử vong trên mỗi 100 người-năm (person-years) quan sát. Để minh họa, chúng ta sử dụng các quan sát trong Bảng 9-1 để xác định số người-tháng sống còn. Bất kể bệnh nhân còn sống hay đã chết vào cuối nghiên cứu, họ đều đóng góp vào việc tính toán trong khoảng thời gian họ đã tham gia nghiên cứu. Do đó, bệnh nhân 1 đóng góp 10,28 tháng, bệnh nhân 2 tham gia nghiên cứu trong 5,55 tháng, và cứ thế tiếp tục. Tổng số tháng bệnh nhân đã được quan sát là 327,65 tháng; chuyển đổi sang năm bằng cách chia cho 12 cho ra 27,3 người-năm.
Một vấn đề với việc sử dụng người-năm quan sát là cùng một con số có thể thu được bằng cách quan sát 1.000 bệnh nhân trong 1 năm hoặc bằng cách quan sát 100 bệnh nhân trong 10 năm. Mặc dù số lượng đối tượng có liên quan đến việc tính toán người-năm, nó không xuất hiện rõ ràng như một phần của kết quả; và không có phương pháp thống kê nào để so sánh những con số này. Một vấn đề khác là giả định cố hữu rằng nguy cơ của một biến cố, chẳng hạn như tử vong hoặc thải ghép, trong bất kỳ đơn vị thời gian nào là không đổi trong suốt nghiên cứu (mặc dù một số phương pháp sống còn khác cũng đưa ra giả định này).
Tỷ lệ tử vong (xem Chương 3) là một cách quen thuộc để xử lý dữ liệu sống còn, và chúng được sử dụng (đặc biệt trong ung thư học) để ước tính tỷ lệ sống còn 3 năm và 5 năm với các loại tình trạng y tế khác nhau. Chúng ta không thể xác định tỷ lệ tử vong bằng cách sử dụng dữ liệu trên tất cả bệnh nhân cho đến khi khoảng thời gian quy định đã trôi qua.
Giả sử chúng ta có một nghiên cứu với 20 bệnh nhân: 10 người sống ít nhất 1 năm, 4 người chết trước 1 năm, và 6 người đã tham gia nghiên cứu dưới một năm (tức là họ bị kiểm duyệt). Chúng ta phải quyết định làm gì với sáu bệnh nhân bị kiểm duyệt để tính tỷ lệ sống còn 1 năm. Một giải pháp là chia số người chết trong năm đầu tiên, 4, cho tổng số người trong nghiên cứu, 20, để có ước tính là 0,20, hay 20%. Tuy nhiên, ước tính này có thể quá thấp, vì nó giả định rằng không ai trong số sáu bệnh nhân tham gia nghiên cứu dưới 1 năm sẽ chết trước khi năm đó kết thúc.
Một giải pháp thay thế là bỏ qua những bệnh nhân không tham gia nghiên cứu đủ 1 năm để có , hay 28,6%. Kỹ thuật này tương tự như cách tiếp cận được sử dụng trong nghiên cứu ung thư, trong đó tỷ lệ tử vong 3 năm và 5 năm chỉ dựa trên những bệnh nhân đã tham gia nghiên cứu ít nhất 3 hoặc 5 năm. Hạn chế của cách tiếp cận này là nó hoàn toàn bỏ qua sự đóng góp của sáu bệnh nhân đã tham gia nghiên cứu trong một phần của năm. Chúng ta cần một cách để sử dụng thông tin thu được từ tất cả các bệnh nhân đã tham gia nghiên cứu. Một cách tiếp cận hợp lý sẽ tạo ra một ước tính nằm giữa 20% và 28,6%, đó chính là những gì phân tích bảng sống tính toán bảo hiểm và phương pháp giới hạn tích Kaplan-Meier làm được. Chúng ghi nhận khoảng thời gian các đối tượng đã sống sót cho đến thời điểm dữ liệu được phân tích.
PHÂN TÍCH TÍNH TOÁN BẢO HIỂM, HAY BẢNG SỐNG
Phân tích tính toán bảo hiểm, hay bảng sống, đôi khi còn được gọi trong y văn là phương pháp Cutler-Ederer (Cutler và Ederer, 1958). Phương pháp tính toán bảo hiểm không quá phức tạp về mặt tính toán và đã từng là phương pháp chủ đạo được sử dụng trong y học. Tuy nhiên, sự sẵn có của máy tính khiến nó ngày nay ít được sử dụng hơn nhiều so với phương pháp giới hạn tích Kaplan-Meier được thảo luận trong phần tiếp theo.
Chúng tôi sẽ minh họa ngắn gọn các tính toán liên quan đến phân tích tính toán bảo hiểm bằng cách sắp xếp 14 bệnh nhân chỉ điều trị bằng regorafenib theo thời gian họ sống sót (Bảng 9-2). Chúng tôi sử dụng các quan sát trong Bảng 9-2 để tạo ra Bảng 9-3. Các khoảng thời gian là tùy ý nhưng nên được chọn sao cho số lượng quan sát bị kiểm duyệt trong bất kỳ khoảng nào là nhỏ; chúng tôi nhóm theo khoảng 5 tháng cho ví dụ này.
Bảng 9-2. Tình trạng sống còn của một mẫu bệnh nhân trong nhánh chỉ dùng regorafenib.
| Ca | Giới tính | Tuổi | Điều trị | Số tháng sống không bệnh tiến triển | Số tháng sống còn toàn bộ | Tình trạng |
|---|---|---|---|---|---|---|
| 8 | Nam | 60 | R | 1.58 | 3.71 | Đã mất |
| 13 | Nam | 55 | R | 0.92 | 5.09 | Đã mất |
| 2 | Nam | 81 | R | 2.99 | 5.55 | Đã mất |
| 3 | Nam | 73 | R | 4.34 | 5.82 | Đã mất |
| 4 | Nam | 58 | R | 4.07 | 8.90 | Đã mất |
| 11 | Nữ | 40 | R | 2.04 | 9.00 | Đã mất |
| 1 | Nữ | 67 | R | 1.61 | 10.28 | Đã mất |
| 5 | Nữ | 54 | R | 2.53 | 10.41 | Đã mất |
| 14 | Nam | 48 | R | 0.69 | 10.55 | Đã mất |
| 18 | Nam | 60 | R | 7.82 | 10.55 | Đã mất |
| 6 | Nam | 43 | R | 2.63 | 10.68 | Đã mất |
| 15 | Nữ | 57 | R | 2.66 | 12.16 | Còn sống |
| 16 | Nam | 60 | R | 2.76 | 13.17 | Đã mất |
| 9 | Nữ | 54 | R | 5.78 | 20.01 | Còn sống |
| Dữ liệu từ Lin C-Y, và cộng sự (2018). | ||||||
Bảng 9-3. Bảng sống cho mẫu 14 bệnh nhân được điều trị bằng regorafenib kết hợp.
| Thời điểm bắt đầu khoảng | Số người tham gia vào khoảng này, |
Số người rút khỏi trong khoảng, |
Số người chịu rủi ro | Số biến cố kết thúc, |
Tỷ lệ kết thúc, |
Tỷ lệ sống sót, |
Tỷ lệ sống sót tích lũy cuối khoảng,
|
|---|---|---|---|---|---|---|---|
| 0 | 14 | 0 | 14.0 | 1 | 0.071 | 0.929 | 0.929 |
| 5 | 13 | 0 | 13.0 | 5 | 0.385 | 0.615 | 0.571 |
| 10 | 8 | 1 | 7.5 | 6 | 0.800 | 0.200 | 0.114 |
| 15 | 1 | 0 | 1.0 | 0 | 0.000 | 1.000 | 0.114 |
| 20 | 1 | 1 | 1.0 | 0 | 0.000 | 1.000 | 0.114 |
| Dữ liệu từ Lin C-Y, và cộng sự (2018). | |||||||
Tiêu đề cột trong Bảng 9-3 là số bệnh nhân trong nghiên cứu vào đầu khoảng thời gian; tất cả bệnh nhân (14) đều bắt đầu nghiên cứu, vì vậy là 14. Một bệnh nhân không hoàn thành khoảng thời gian đầu tiên: bệnh nhân 8. Bệnh nhân 8 đã qua đời, được gọi là một biến cố kết thúc (terminal event) (); không có trường hợp rút lui nào trong giai đoạn này ().
Phương pháp tính toán bảo hiểm giả định rằng bệnh nhân rút lui một cách ngẫu nhiên trong suốt khoảng thời gian; do đó, trung bình, họ rút lui vào giữa khoảng thời gian đó. Theo một nghĩa nào đó, phương pháp này ghi nhận cho những bệnh nhân rút lui đã tham gia nghiên cứu trong một nửa khoảng thời gian. Một nửa số bệnh nhân rút lui được trừ đi khỏi số bệnh nhân bắt đầu khoảng thời gian, vì vậy mẫu số được sử dụng để tính tỷ lệ có biến cố kết thúc được giảm đi một nửa số người rút lui trong giai đoạn đó. Trong giai đoạn bắt đầu từ 10, có một trường hợp rút lui (ca 15). Tám đối tượng bắt đầu khoảng thời gian, vì vậy , hay 7.5 là số đối tượng chịu rủi ro trong ví dụ của chúng ta. Tỷ lệ kết thúc là . Tỷ lệ sống sót là , và tỷ lệ sống sót tích lũy là . Quy trình tính toán này tiếp tục cho đến khi bảng được hoàn thành.
Lưu ý rằng là xác suất chỉ sống sót qua khoảng i; và để sống sót qua khoảng i, một bệnh nhân phải đã sống sót qua tất cả các khoảng trước đó. Do đó, là một ví dụ về xác suất có điều kiện vì xác suất sống sót qua khoảng i phụ thuộc, hoặc có điều kiện, vào việc sống sót cho đến thời điểm đó. Xác suất này đôi khi được gọi là hàm sống còn (survival function). Nhớ lại từ Chương 4 rằng nếu một sự kiện có điều kiện vào một sự kiện trước đó, xác suất xảy ra đồng thời của chúng được tìm thấy bằng cách nhân xác suất của sự kiện có điều kiện với xác suất của sự kiện trước đó. Do đó, xác suất tích lũy để sống sót qua khoảng i cộng với tất cả các khoảng trước đó được tìm thấy bằng cách nhân với .
Kết quả từ một phân tích tính toán bảo hiểm có thể giúp trả lời các câu hỏi có thể giúp các bác sĩ lâm sàng tư vấn cho bệnh nhân hoặc gia đình họ. Ví dụ, chúng ta có thể hỏi, Nếu X là thời gian sống sót của một bệnh nhân được chọn ngẫu nhiên từ quần thể được đại diện bởi những bệnh nhân này, xác suất để X là 5 tháng hoặc lớn hơn là bao nhiêu? Từ Bảng 9-3, xác suất một bệnh nhân sẽ sống ít nhất 5 tháng là khoảng 0,57.
Các bài báo khoa học hiếm khi trình bày kết quả từ phân tích bảng sống như chúng ta đã làm trong Bảng 9-3; thay vào đó, kết quả thường được trình bày dưới dạng một đường cong sống còn. Đường trong Hình 9-3 là một đường cong sống còn cho mẫu 14 bệnh nhân chỉ dùng regorafenib.
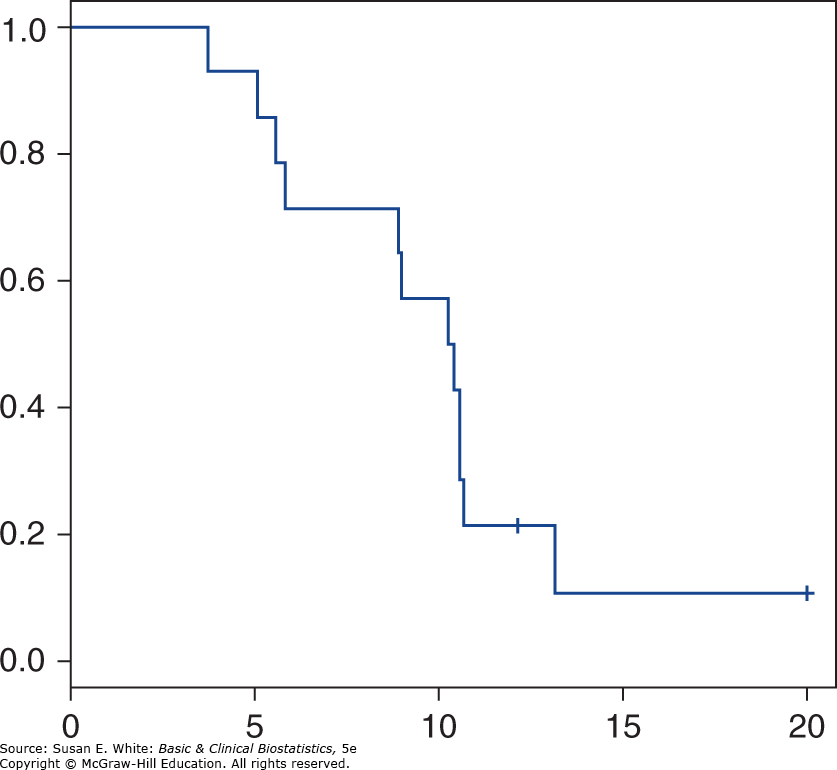
Hình 9-3. Biểu đồ sống còn theo bảng sống của một mẫu bệnh nhân trong nhánh regorafenib.
Phương pháp tính toán bảo hiểm bao gồm hai giả định về dữ liệu. Thứ nhất là tất cả các trường hợp rút lui trong một khoảng thời gian nhất định xảy ra, trung bình, tại điểm giữa của khoảng thời gian đó. Giả định này ít quan trọng hơn khi các khoảng thời gian phân tích ngắn; tuy nhiên, sai lệch đáng kể có thể xảy ra nếu các khoảng thời gian lớn, nếu có nhiều trường hợp rút lui, và nếu các trường hợp rút lui không xảy ra ở giữa khoảng thời gian. Phương pháp Kaplan-Meier được giới thiệu trong phần tiếp theo khắc phục được vấn đề này. Giả định thứ hai là, mặc dù sự sống còn trong một giai đoạn nhất định phụ thuộc vào sự sống còn trong tất cả các giai đoạn trước đó, xác suất sống sót tại một giai đoạn được coi như là độc lập với xác suất sống sót tại các giai đoạn khác. Điều kiện này, mặc dù có thể bị vi phạm phần nào trong nhiều nghiên cứu y học, dường như không gây ra mối quan tâm lớn cho các nhà thống kê sinh học.
PHƯƠNG PHÁP GIỚI HẠN TÍCH KAPLAN-MEIER
Phương pháp ước tính sự sống còn của Kaplan-Meier tương tự như phân tích tính toán bảo hiểm ngoại trừ việc thời gian kể từ khi tham gia nghiên cứu không được chia thành các khoảng để phân tích. Tùy thuộc vào số lượng bệnh nhân đã qua đời, phương pháp giới hạn tích Kaplan-Meier, thường được gọi là đường cong Kaplan-Meier, có thể bao gồm ít tính toán hơn phương pháp tính toán bảo hiểm, chủ yếu là vì sự sống còn được ước tính mỗi khi một bệnh nhân qua đời, do đó các trường hợp rút lui bị bỏ qua. Chúng tôi sẽ minh họa bằng dữ liệu từ Lin và cộng sự (2018) sử dụng cùng một tập hợp con bệnh nhân như với phân tích bảng sống, tức là những bệnh nhân chỉ dùng regorafenib.
Bước đầu tiên là liệt kê các thời điểm xảy ra tử vong hoặc bỏ cuộc, như trong cột “Thời gian biến cố” trong Bảng 9-4. Một bệnh nhân qua đời tại 3,71 tháng và một người khác tại 5,09 tháng, và chúng được liệt kê dưới cột “Số biến cố”. Sau đó, mỗi khi một biến cố hoặc kết cục xảy ra, tỷ lệ tử vong, tỷ lệ sống sót và tỷ lệ sống sót tích lũy được tính toán theo cách tương tự như với phương pháp bảng sống. Nếu bảng được công bố trong một bài báo, nó thường được định dạng ở dạng rút gọn, như trong Bảng 9-5.
Bảng 9-4. Đường cong sống còn Kaplan-Meier chi tiết cho bệnh nhân chỉ dùng regorafenib.
| Thời gian biến cố (T) | Số người chịu rủi ro | Số biến cố | Tỷ lệ tử vong | Tỷ lệ sống sót | Tỷ lệ sống sót tích lũy |
|---|---|---|---|---|---|
| 3.710 | 14 | 1 | 0.071 | 0.929 | 0.929 |
| 5.090 | 13 | 1 | 0.077 | 0.923 | 0.857 |
| 5.550 | 12 | 1 | 0.083 | 0.917 | 0.786 |
| 5.820 | 11 | 1 | 0.091 | 0.909 | 0.714 |
| 8.900 | 10 | 1 | 0.100 | 0.900 | 0.643 |
| 9.000 | 9 | 1 | 0.111 | 0.889 | 0.571 |
| 10.280 | 8 | 1 | 0.125 | 0.875 | 0.500 |
| 10.410 | 7 | 1 | 0.143 | 0.857 | 0.429 |
| 10.550 | 6 | 1 | 0.167 | 0.833 | 0.357 |
| 10.550 | 5 | 1 | 0.200 | 0.800 | 0.286 |
| 10.680 | 4 | 1 | 0.250 | 0.750 | 0.214 |
| 12.160 | 3 | 0 | |||
| 13.170 | 2 | 1 | 0.500 | 0.500 | 0.107 |
| 20.010 | 1 | 0 | |||
| Dữ liệu từ Lin C-Y, và cộng sự (2018). | |||||
Bảng 9-5. Phân tích sống còn cho OSM (số tháng sống còn) ở cả hai nhánh điều trị.
Điều trị = C
| Thời gian | n.risk | n.event | survival | std.err | KTC 95% dưới | KTC 95% trên |
|---|---|---|---|---|---|---|
| 3.52 | 34 | 1 | 0.971 | 0.0290 | 0.915 | 1.000 |
| 3.98 | 33 | 1 | 0.941 | 0.0404 | 0.865 | 1.000 |
| 4.04 | 32 | 1 | 0.912 | 0.0456 | 0.821 | 1.000 |
| 4.30 | 31 | 1 | 0.882 | 0.0553 | 0.780 | 0.998 |
| 4.44 | 30 | 1 | 0.853 | 0.0607 | 0.742 | 0.981 |
| 4.99 | 28 | 1 | 0.822 | 0.0658 | 0.703 | 0.962 |
| 6.83 | 23 | 1 | 0.787 | 0.0720 | 0.658 | 0.941 |
| 7.13 | 22 | 1 | 0.751 | 0.0771 | 0.614 | 0.918 |
| 9.43 | 19 | 1 | 0.711 | 0.0825 | 0.567 | 0.893 |
| 10.61 | 17 | 1 | 0.670 | 0.0876 | 0.518 | 0.865 |
| 11.20 | 16 | 1 | 0.628 | 0.0916 | 0.472 | 0.836 |
| 11.30 | 14 | 1 | 0.583 | 0.0954 | 0.423 | 0.803 |
| 13.54 | 8 | 1 | 0.510 | 0.1078 | 0.337 | 0.772 |
| 20.90 | 2 | 1 | 0.255 | 0.1882 | 0.060 | 1.000 |
Điều trị = R
| Thời gian | n.risk | n.event | survival | std.err | KTC 95% dưới | KTC 95% trên |
|---|---|---|---|---|---|---|
| 2.89 | 27 | 1 | 0.963 | 0.0363 | 0.8943 | 1.000 |
| 3.71 | 26 | 1 | 0.926 | 0.0504 | 0.8322 | 1.000 |
| 4.37 | 25 | 1 | 0.889 | 0.0605 | 0.7779 | 1.000 |
| 4.96 | 24 | 2 | 0.815 | 0.0748 | 0.6807 | 0.975 |
| 5.09 | 22 | 1 | 0.778 | 0.0800 | 0.6358 | 0.952 |
| 5.55 | 18 | 1 | 0.735 | 0.0864 | 0.5833 | 0.925 |
| 5.82 | 16 | 1 | 0.689 | 0.0924 | 0.5294 | 0.896 |
| 6.14 | 15 | 1 | 0.643 | 0.0970 | 0.4782 | 0.864 |
| 8.90 | 12 | 1 | 0.589 | 0.1027 | 0.4187 | 0.829 |
| 9.00 | 11 | 1 | 0.536 | 0.1064 | 0.3629 | 0.791 |
| 10.28 | 10 | 1 | 0.482 | 0.1084 | 0.3102 | 0.749 |
| 10.41 | 9 | 1 | 0.428 | 0.1088 | 0.2605 | 0.705 |
| 10.55 | 8 | 2 | 0.321 | 0.1047 | 0.1697 | 0.609 |
| 10.68 | 6 | 1 | 0.268 | 0.1000 | 0.1288 | 0.557 |
| 13.17 | 2 | 1 | 0.134 | 0.1071 | 0.0279 | 0.642 |
| Điều trị: C, điều trị kết hợp; R, regorafenib đơn độc. Dữ liệu từ Lin C-Y, và cộng sự (2018). | ||||||
Lưu ý rằng phương pháp Kaplan-Meier cho tỷ lệ sống còn chính xác vì nó sử dụng thời gian sống còn chính xác; phương pháp tính toán bảo hiểm cho các giá trị gần đúng vì nó nhóm các thời gian sống còn thành các khoảng. Trước khi máy tính được sử dụng rộng rãi, phương pháp tính toán bảo hiểm dễ sử dụng hơn nhiều đối với một số lượng lớn các quan sát.
Thông thường, khi khoảng thời gian từ lúc tham gia nghiên cứu trở nên dài hơn, số lượng bệnh nhân còn lại trong nghiên cứu ngày càng nhỏ đi. Điều này có nghĩa là độ lệch chuẩn của ước tính tỷ lệ sống sót ngày càng lớn hơn theo thời gian. Đôi khi, số lượng bệnh nhân còn lại trong nghiên cứu được in dưới trục thời gian. Một số tác giả cung cấp các biểu đồ với các đường đứt nét ở hai bên của đường cong sống còn đại diện cho khoảng tin cậy 95% cho đường cong. Các giới hạn tin cậy trở nên rộng hơn khi thời gian trôi qua, phản ánh sự giảm sút độ tin cậy trong ước tính tỷ lệ khi cỡ mẫu giảm. Những thực hành này là mong muốn, nhưng không phải tất cả các chương trình máy tính đều cung cấp chúng.
Để minh họa các khoảng tin cậy, chúng tôi phân tích sự sống còn thực tế của tất cả bệnh nhân trong cả hai nhánh điều trị. Quy trình để có được các khoảng tin cậy sử dụng sai số chuẩn của ước tính sống còn tích lũy .
Ví dụ, tại tháng thứ 4, 13 bệnh nhân dùng liệu pháp kết hợp vẫn còn trong nghiên cứu và 1 bệnh nhân đã qua đời, vì vậy:
và sai số chuẩn là:
Các tính toán còn lại cho cả hai nhánh điều trị được đưa ra trong Bảng 9-5.
Hình 9-4 là một biểu đồ của đường cong giới hạn tích Kaplan-Meier cho tất cả bệnh nhân chỉ dùng regorafenib minh họa các khoảng tin cậy 95%. Trong biểu đồ này, đường cong có dạng bậc thang vì tỷ lệ bệnh nhân sống sót thay đổi chính xác tại các thời điểm một đối tượng qua đời.
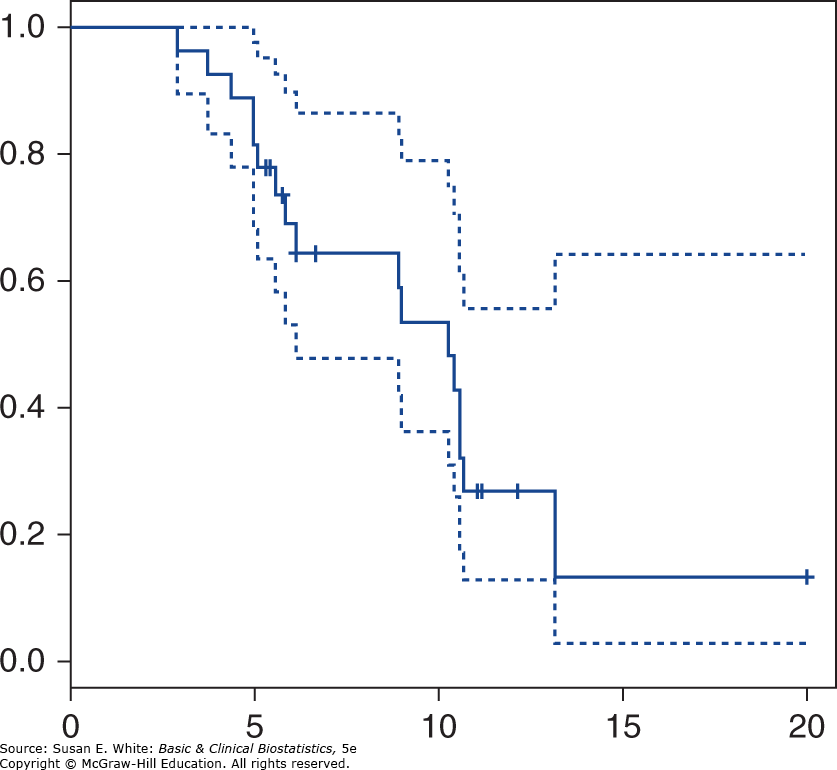
Hình 9-4. Đường cong Kaplan-Meier với giới hạn tin cậy 95% cho bệnh nhân chỉ dùng regorafenib.
SO SÁNH HAI ĐƯỜNG CONG SỐNG CÒN
Mặc dù một số bài báo khoa học chỉ báo cáo sự sống còn cho một nhóm, các nhà điều tra thường muốn so sánh hai hoặc nhiều mẫu bệnh nhân. Bảng 9-6 chứa phân tích sống còn cho toàn bộ mẫu 61 bệnh nhân, phân chia theo từng nhánh điều trị (Lin và cộng sự, 2018).
Bảng 9-6. Thống kê Logrank cho sự sống còn.
| Tháng | Số người chịu rủi ro (C) | Số người chịu rủi ro (R) | Tổng | Số ca tử vong quan sát (C) | Số ca tử vong quan sát (R) | Tổng | Số ca tử vong kỳ vọng (C) | Số ca tử vong kỳ vọng (R) | Tổng |
|---|---|---|---|---|---|---|---|---|---|
| 2.89 | 34 | 27 | 61 | 0 | 1 | 1 | 0.557 | 0.443 | 1 |
| 3.52 | 34 | 26 | 60 | 1 | 0 | 1 | 0.567 | 0.433 | 1 |
| 3.71 | 33 | 26 | 59 | 0 | 1 | 1 | 0.559 | 0.441 | 1 |
| 3.98 | 33 | 25 | 58 | 1 | 0 | 1 | 0.569 | 0.431 | 1 |
| 4.04 | 32 | 25 | 57 | 1 | 0 | 1 | 0.561 | 0.439 | 1 |
| 4.30 | 31 | 25 | 56 | 1 | 0 | 1 | 0.554 | 0.446 | 1 |
| 4.37 | 30 | 25 | 55 | 0 | 1 | 1 | 0.545 | 0.455 | 1 |
| 4.44 | 30 | 24 | 54 | 1 | 0 | 1 | 0.556 | 0.444 | 1 |
| 4.96 | 29 | 24 | 53 | 0 | 2 | 2 | 1.094 | 0.906 | 2 |
| 4.99 | 28 | 22 | 50 | 1 | 0 | 1 | 0.560 | 0.440 | 1 |
| 5.09 | 27 | 22 | 49 | 0 | 1 | 1 | 0.551 | 0.449 | 1 |
| 5.55 | 26 | 18 | 44 | 0 | 1 | 1 | 0.591 | 0.409 | 1 |
| 5.82 | 26 | 16 | 42 | 0 | 1 | 1 | 0.619 | 0.381 | 1 |
| 6.14 | 25 | 15 | 40 | 0 | 1 | 1 | 0.625 | 0.375 | 1 |
| 6.83 | 23 | 12 | 35 | 1 | 0 | 1 | 0.657 | 0.343 | 1 |
| 7.13 | 22 | 12 | 34 | 1 | 0 | 1 | 0.647 | 0.353 | 1 |
| 8.90 | 21 | 12 | 33 | 0 | 1 | 1 | 0.636 | 0.364 | 1 |
| 9.00 | 21 | 11 | 32 | 0 | 1 | 1 | 0.656 | 0.344 | 1 |
| 9.43 | 19 | 10 | 29 | 1 | 0 | 1 | 0.655 | 0.345 | 1 |
| 10.28 | 17 | 10 | 27 | 0 | 1 | 1 | 0.630 | 0.370 | 1 |
| 10.41 | 17 | 9 | 26 | 0 | 1 | 1 | 0.654 | 0.346 | 1 |
| 10.55 | 17 | 8 | 25 | 0 | 2 | 2 | 1.360 | 0.640 | 2 |
| 10.61 | 17 | 6 | 23 | 1 | 0 | 1 | 0.739 | 0.261 | 1 |
| 10.68 | 16 | 6 | 22 | 0 | 1 | 1 | 0.727 | 0.273 | 1 |
| 11.20 | 16 | 3 | 19 | 1 | 0 | 1 | 0.842 | 0.158 | 1 |
| 11.30 | 14 | 3 | 17 | 1 | 0 | 1 | 0.824 | 0.176 | 1 |
| 13.17 | 8 | 2 | 10 | 0 | 1 | 1 | 0.800 | 0.200 | 1 |
| 13.54 | 8 | 1 | 9 | 1 | 0 | 1 | 0.889 | 0.111 | 1 |
| 20.90 | 2 | 0 | 2 | 1 | 0 | 1 | 1.000 | 1 | |
| Tổng cộng | 14 | 17 | 31 | 20.225 | 10.775 |
Tính toán thống kê logrank
| O-E | Tổng | p-value | |||
|---|---|---|---|---|---|
| C | (6.23) | 38.75 | 1.92 | 5.51 | 0.018882 |
| R | 6.23 | 38.75 | 3.60 | ||
| Dữ liệu từ Lin C-Y, và cộng sự (2018). | |||||
Các đường cong sống còn Kaplan-Meier cho cả hai nhánh điều trị được đưa ra trong Hình 9-5. Rất khó để biết bằng mắt thường liệu hai đường cong có khác biệt đáng kể hay không. Chúng ta không thể đưa ra nhận định chỉ dựa trên khoảng cách giữa hai đường; một sự khác biệt nhỏ có thể có ý nghĩa thống kê nếu cỡ mẫu lớn, và một sự khác biệt lớn có thể không có ý nghĩa nếu cỡ mẫu nhỏ. Như bạn có thể đoán, chúng ta cần thực hiện một kiểm định thống kê để đánh giá mức độ của bất kỳ sự khác biệt nào.
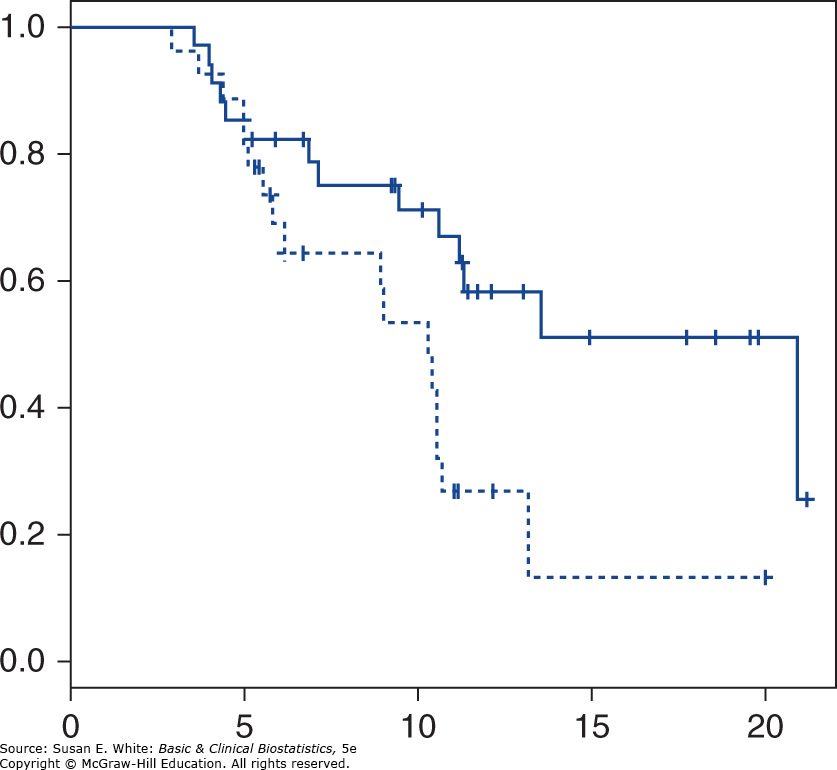
Hình 9-5. Đường cong sống còn Kaplan-Meier của bệnh nhân trong cả hai nhánh điều trị.
Chúng ta cần các phương pháp đặc biệt để so sánh các phân phối sống còn. Nếu không có quan sát bị kiểm duyệt nào xảy ra, kiểm định tổng hạng Wilcoxon được giới thiệu trong Chương 6 là phù hợp để so sánh các hạng của thời gian sống còn. Kiểm định t cho các nhóm độc lập không phù hợp vì thời gian sống còn không tuân theo phân phối chuẩn và có xu hướng lệch dương (trong một số trường hợp là rất lệch).
Nếu một số quan sát bị kiểm duyệt, có thể sử dụng một số phương pháp để so sánh các đường cong sống còn. Hầu hết các bài báo trong y văn báo cáo so sánh các đường cong sống còn bằng cách sử dụng thống kê logrank hoặc thống kê chi-bình phương Mantel-Haenszel. Các tính toán cho tất cả các phương pháp đều rất tốn thời gian, và các chương trình máy tính có sẵn. Chúng tôi sẽ minh họa các phương pháp logrank và Mantel-Haenszel; cả hai phương pháp đều đơn giản, mặc dù tính toán nặng nề, và hữu ích trong việc giúp chúng ta hiểu logic đằng sau phương pháp. Trong bối cảnh của thống kê logrank, chúng tôi minh họa tỷ số nguy cơ (hazard ratio), một thống kê mô tả hữu ích để so sánh hai nhóm có nguy cơ.
Phép kiểm Logrank
Một số dạng của thống kê logrank đã được các nhà thống kê sinh học khác nhau công bố, vì vậy nó được gọi bằng nhiều tên khác nhau trong y văn: thống kê logrank Mantel, thống kê logrank Cox-Mantel, và đơn giản là thống kê logrank. Phép kiểm logrank so sánh số ca tử vong quan sát được trong mỗi nhóm với số ca tử vong được kỳ vọng dựa trên số ca tử vong trong các nhóm kết hợp, tức là, nếu tư cách thành viên nhóm không quan trọng. Một phép kiểm chi-bình phương gần đúng được sử dụng để kiểm tra ý nghĩa của một biểu thức toán học liên quan đến số ca tử vong quan sát và kỳ vọng.
Để minh họa phép kiểm logrank, chúng tôi tiếp tục sử dụng dữ liệu từ Lin và cộng sự (2018). Chúng tôi đã nhóm dữ liệu cho toàn bộ mẫu 61 bệnh nhân trong nghiên cứu sử dụng cùng các nhóm đã được trình bày trước đó trong bảng sống ở Bảng 9-3; các bước để tính toán thống kê logrank như sau.
- Tạo các hàng cho mỗi khoảng thời gian có một bệnh nhân qua đời ở một trong hai phương pháp điều trị. Cột thứ hai và thứ ba chứa số lượng bệnh nhân trong mỗi nhóm có nguy cơ tử vong trong khoảng thời gian đó. Mỗi hàng sẽ được giảm đi số lượng đối tượng tử vong cũng như số lượng người rút lui hoặc bị kiểm duyệt.
- Trong các cột từ 5 đến 7, số lượng bệnh nhân trong mỗi nhóm đã qua đời trong khoảng thời gian đó và tổng số được liệt kê. Tính toán này tiếp tục qua tất cả các giai đoạn.
- Ba cột cuối cùng chứa số ca tử vong kỳ vọng cho mỗi nhóm và tổng số tại mỗi giai đoạn. Số ca tử vong kỳ vọng cho một nhóm nhất định được tìm thấy bằng cách nhân tổng số ca tử vong trong một giai đoạn nhất định với tỷ lệ bệnh nhân trong nhóm đó. Ví dụ, tại 9 tháng, 21 bệnh nhân vẫn còn trong nhóm C và 11 trong nhóm R, tổng cộng là 32. Một ca tử vong được ghi nhận; vì vậy là số ca tử vong kỳ vọng xảy ra trong nhóm C, và là số ca tử vong kỳ vọng trong nhóm R. Tính toán này được thực hiện cho tất cả các giai đoạn.
- Tổng số được tính cho mỗi cột.
Biểu thức sau có thể được sử dụng để kiểm tra giả thuyết không rằng các phân phối sống còn là như nhau trong hai nhóm:
trong đó là tổng số ca tử vong quan sát được trong nhóm C, là tổng số ca tử vong kỳ vọng trong nhóm C, và cứ thế tiếp tục. Thống kê tuân theo một phân phối chi-bình phương gần đúng với 1 bậc tự do. Trong ví dụ của chúng ta, tính được:
Phân phối chi-bình phương với 1 bậc tự do trong Bảng A-5 chỉ ra rằng giá trị tới hạn là 3,841 là cần thiết để có ý nghĩa ở mức 0,05. Do đó, chúng tôi kết luận rằng có một sự khác biệt có ý nghĩa thống kê trong các phân phối thời gian sống còn toàn bộ của bệnh nhân trải qua hai phác đồ điều trị.
Tỷ số nguy cơ (Hazard Ratio)
Một lợi ích của việc tính toán thống kê logrank là tỷ số nguy cơ có thể dễ dàng được tính toán từ thông tin được cung cấp trong Bảng 9-6.
Nó được ước tính bằng công thức:
Trong ví dụ của chúng ta, tỷ số nguy cơ, hay nguy cơ tử vong ở bệnh nhân chỉ được điều trị bằng regorafenib so với điều trị kết hợp là:
Tỷ số nguy cơ 2,28 có thể được diễn giải theo cách tương tự như tỷ số chênh: Nguy cơ tử vong tại bất kỳ thời điểm nào trong nhóm chỉ dùng phác đồ regorafenib cao hơn khoảng hai lần so với nguy cơ trong nhóm điều trị kết hợp. Việc sử dụng tỷ số nguy cơ giả định rằng nguy cơ tử vong là như nhau trong suốt thời gian nghiên cứu; chúng ta sẽ thảo luận lại về khái niệm nguy cơ trong chương tiếp theo.
Thống kê Chi-bình phương Mantel-Haenszel
Một phương pháp khác để so sánh các phân phối sống còn là một ước tính của tỷ số chênh được phát triển bởi Mantel và Haenszel, tuân theo (gần đúng) một phân phối chi-bình phương với 1 bậc tự do. Phép kiểm Mantel-Haenszel kết hợp một loạt các bảng được hình thành tại các thời điểm sống còn khác nhau thành một phép kiểm tổng thể về ý nghĩa của các đường cong sống còn. Thống kê Mantel-Haenszel rất hữu ích vì nó có thể được sử dụng để so sánh bất kỳ phân phối nào, không chỉ riêng đường cong sống còn.
Chúng tôi lại sử dụng dữ liệu từ Lin và cộng sự (2018) để minh họa việc tính toán thống kê Mantel-Haenszel (Bảng 9-7). Bước đầu tiên là chọn các khoảng thời gian để hình thành các bảng ; chúng tôi sử dụng các khoảng 5 tháng như được hiển thị trong ví dụ bảng sống. Đối với mỗi khoảng, số bệnh nhân còn sống và số người qua đời là các hàng, và số bệnh nhân trong mỗi nhóm là các cột của các bảng .
Bảng 9-7. Minh họa Mantel-Haenszel sử dụng toàn bộ mẫu.
| Khoảng thời gian | Tình trạng | Nhóm C | Nhóm R | Tổng | Tỷ số chênh () | Tỷ số chênh () | Quan sát | Kỳ vọng | Phương sai |
|---|---|---|---|---|---|---|---|---|---|
| 0-5 | Còn sống | 28 | 19 | 47 | 3.672131 | 1.868852 | 28 | 26.19672 | 2.705563 |
| Đã mất | 6 | 8 | 14 | ||||||
| Tổng | 34 | 27 | 61 | ||||||
| 6-10 | Còn sống | 22 | 12 | 34 | 1.65 | 0.9 | 22 | 21.25 | 1.225962 |
| Đã mất | 3 | 3 | 6 | ||||||
| Tổng | 25 | 15 | 40 | ||||||
| 11-15 | Còn sống | 13 | 2 | 15 | 0.684211 | 0.315789 | 13 | 12.63158 | 0.443213 |
| Đã mất | 3 | 1 | 4 | ||||||
| Tổng | 16 | 3 | 19 | ||||||
| Tổng | 6.006342 | 3.084642 | 63 | 60.0783 | 4.374738 | ||||
| Mantel-Haenszel | 1.951278 |
Cũng như phép kiểm logrank, phép kiểm Mantel-Haenszel rất nặng về tính toán. Bước đầu tiên ước tính một tỷ số chênh gộp, hữu ích cho mục đích mô tả nhưng không cần thiết cho chính phép kiểm thống kê.
Tỷ số chênh gộp là:
trong đó a, b, c, d, và n được định nghĩa như trong bảng ở Bảng 6-9. Tử số và mẫu số được tính trong các cột dưới tiêu đề “Tỷ số chênh”. Đối với khoảng thời gian đầu tiên, ad/n là hay 3,67. Tổng các số hạng trong tử số là 6,00 và trong mẫu số là 3,08. Do đó, ước tính của tỷ số chênh bằng cách sử dụng phương pháp Mantel-Haenszel là 6,00/3,08 = 1,95. Giả thuyết cần kiểm tra là liệu 1,95 có khác biệt đáng kể so với 1 hay không.
Các tính toán còn lại tập trung vào ô (1, 1) của bảng; chúng ta trước tiên tìm giá trị kỳ vọng và phương sai của nó cho mỗi bảng . Ví dụ, từ 6 đến 10 tháng, trong số 25 bệnh nhân dùng liệu pháp kết hợp còn sống và đã tham gia nghiên cứu ít nhất 6 tháng, 22 người vẫn sống và 3 người qua đời trong giai đoạn đó. Trong số 15 người chỉ dùng liệu pháp regorafenib, 12 người vẫn sống và 3 người qua đời. Các giá trị kỳ vọng được tìm thấy theo cách tương tự như trong phép kiểm chi-bình phương đã thảo luận trong Chương 5 và 6. Ví dụ, giá trị kỳ vọng của ô (1, 1) trong giai đoạn này là tổng hàng nhân với tổng cột chia cho tổng chung:
Ngoài ra, phương sai của ô (1, 1) được tính. Sử dụng ký hiệu từ Bảng 6-9, phương sai ước tính là:
Đối với giai đoạn này, phương sai, với làm tròn, là:
Sau khi giá trị kỳ vọng và phương sai được tìm thấy cho mỗi bảng , các giá trị được cộng lại, cùng với số bệnh nhân quan sát được trong ô (1, 1) trong mỗi bảng. Ba tổng là 63, 60,08, và 4,37, như bạn có thể thấy trong Bảng 9-7. Phép kiểm Mantel-Haenszel là bình phương của hiệu số giữa tổng số quan sát và tổng số kỳ vọng, tất cả chia cho tổng các phương sai:
Giá trị này nhỏ hơn giá trị chúng ta tìm thấy cho phép kiểm logrank, và nó không còn có ý nghĩa thống kê. Nhớ lại rằng giá trị tới hạn cho thống kê chi-bình phương với một bậc tự do là 3,841 ở mức 0,05. Chúng ta nên sử dụng thống kê nào? Đó không phải là một lựa chọn đơn giản. Chúng tôi sẽ đưa ra một số hướng dẫn chung trong phần tiếp theo.
Tóm tắt các Quy trình để So sánh các Phân phối Sống còn
Các thống kê logrank được sử dụng rất thường xuyên trong y văn. Một số phương pháp logrank được thấy trong y văn, chẳng hạn như phương pháp được phát triển bởi Peto và Peto (1972). Quy trình logrank gán trọng số như nhau cho tất cả các tính toán, bất kể thời điểm xảy ra một biến cố. Ngược lại, phép kiểm logrank Peto gán trọng số cho các số hạng (quan sát trừ kỳ vọng) bằng số bệnh nhân có nguy cơ tại thời điểm đó, do đó gán nhiều trọng số hơn cho các biến cố sớm khi số bệnh nhân có nguy cơ lớn. Một số nhà thống kê sinh học chọn phương pháp này vì họ tin rằng các tính toán dựa trên cỡ mẫu lớn hơn nên nhận được nhiều trọng số hơn các tính toán dựa trên cỡ mẫu nhỏ hơn xảy ra sau này. Nếu mô hình tử vong tương tự theo thời gian, thống kê logrank Peto và thống kê logrank chúng tôi đã minh họa trước đó thường dẫn đến cùng một kết luận. Tuy nhiên, nếu một tỷ lệ tử vong cao hơn xảy ra trong một khoảng thời gian, chẳng hạn như đôi khi xảy ra sớm trong đường cong sống còn, phép kiểm logrank Peto và phép kiểm logrank có thể khác nhau.
Thực tế, thông tin có sẵn để hướng dẫn các nhà điều tra quyết định quy trình nào là phù hợp trong bất kỳ ứng dụng nào là khá phức tạp, và trong một số tình huống, độc giả của các bài báo khoa học không thể xác định quy trình nào thực sự đã được sử dụng. Thật không may là nhiều quy trình thống kê được sử dụng để so sánh các phân phối sống còn được gọi bằng nhiều tên khác nhau. Một phần của sự nhầm lẫn đã xảy ra vì cùng một các nhà thống kê sinh học (ví dụ: Mantel, Gehan, Cox, Peto và Peto, Haenszel) là hoặc đã là những nhà nghiên cứu hàng đầu đã phát triển một số phép kiểm thống kê. Một nguồn nhầm lẫn khác là nghiên cứu về các phương pháp thống kê sinh học để phân tích dữ liệu sống còn vẫn đang được tiến hành; kết quả là, quy trình Mantel và quy trình logrank Peto chỉ mới được chứng minh là tương đương gần đây.
Phép kiểm chi-bình phương Mantel-Haenszel đôi khi được gọi là phép kiểm logrank trong một số văn bản, và mặc dù về mặt kỹ thuật nó khác biệt, trong nhiều trường hợp nó dẫn đến cùng một kết luận. Thống kê này thực sự có thể được coi là một sự mở rộng của phép kiểm logrank vì nó có thể được sử dụng trong các tình huống tổng quát hơn.
Ví dụ, phép kiểm chi-bình phương Mantel-Haenszel có thể được sử dụng để kết hợp hai hoặc nhiều bảng trong các tình huống khác, chẳng hạn như một bảng cho nam và một bảng cho nữ. Quy trình này tương tự như các phương pháp khác để kiểm soát các yếu tố gây nhiễu, các chủ đề được thảo luận trong Chương 10.
Tóm lại, tất cả các phép kiểm logrank, bất kể chúng được gọi là gì, và phép kiểm chi-bình phương Mantel-Haenszel có thể được coi là các quy trình tương tự. Tuy nhiên, các phép kiểm Gehan và Wilcoxon về mặt khái niệm là khác nhau. Phép kiểm Gehan, hay Wilcoxon tổng quát, là một sự mở rộng của phép kiểm tổng hạng Wilcoxon được minh họa trong Chương 6 được sửa đổi để nó có thể được sử dụng với các quan sát bị kiểm duyệt (Gehan, 1965). Phép kiểm này cũng được gọi trong y văn là phép kiểm Breslow hoặc phép kiểm Kruskal-Wallis tổng quát để so sánh nhiều hơn hai mẫu (Kalbfleisch và Prentice, 2002). Cũng như phép kiểm logrank Peto, phép kiểm Wilcoxon tổng quát sử dụng số bệnh nhân có nguy cơ làm trọng số và, do đó, tính các tổn thất xảy ra sớm trong phân phối sống còn nặng hơn các tổn thất xảy ra muộn.
Một sự khác biệt khác giữa hai họ phép kiểm này là thống kê logrank giả định rằng tỷ lệ của các tỷ lệ nguy cơ trong hai nhóm không đổi trong suốt giai đoạn quan tâm. Khi không thể giả định một tỷ lệ nguy cơ không đổi, quy trình Wilcoxon tổng quát được ưu tiên hơn. Trong tình huống đặc biệt mà các tỷ lệ nguy cơ là tỷ lệ thuận, một phương pháp gọi là mô hình nguy cơ tỷ lệ thuận của Cox có thể được sử dụng; nó ngày càng được sử dụng nhiều trong y văn vì nó cho phép các nhà điều tra kiểm soát các biến gây nhiễu (xem Chương 10).
Như bạn có thể thấy, vấn đề này rất phức tạp và minh họa cho sự cần thiết của việc tham khảo ý kiến một nhà thống kê nếu thực hiện một phân tích sống còn. Quay trở lại câu hỏi của chúng ta trong phần trước khi so sánh bệnh nhân trên hai phác đồ điều trị ung thư ruột kết di căn, chúng ta nên chấp nhận kết quả từ phép kiểm logrank, có ý nghĩa thống kê, hay phép kiểm Mantel-Haenszel, không có ý nghĩa? Nhìn vào sự phân bố của tỷ lệ tử vong qua các giai đoạn thời gian trong Bảng 9-6, một nguy cơ không đổi dường như là một giả định hợp lý. Do đó, chúng tôi sẽ chọn thống kê logrank và kết luận các phương pháp điều trị là khác nhau ở như Lin và cộng sự (2018) đã làm.
HÀM NGUY CƠ TRONG PHÂN TÍCH SỐNG CÒN
Trong phần giới thiệu của chương này, chúng tôi đã nêu rằng việc tính toán thời gian sống còn trung bình thường không hữu ích, và sau đó chúng tôi đã minh họa cách giá trị của nó phụ thuộc vào thời điểm dữ liệu được phân tích. Tuy nhiên, các ước tính về thời gian sống còn trung bình hợp lý có thể thu được khi cỡ mẫu khá lớn. Quy trình này phụ thuộc vào hàm nguy cơ (hazard function), là xác suất một người qua đời trong khoảng thời gian i đến , với điều kiện người đó đã sống sót cho đến thời điểm i. Hàm nguy cơ còn được gọi là tỷ lệ thất bại có điều kiện (conditional failure rate); trong dịch tễ học, thuật ngữ lực tử vong (force of mortality) được sử dụng.
Mặc dù phân phối xác suất mũ không được thảo luận trong Chương 4 khi chúng tôi giới thiệu các phân phối xác suất khác (tức là, phân phối chuẩn, nhị thức, và Poisson), nhiều đường cong sống còn tuân theo một phân phối mũ. Đó là một phân phối liên tục liên quan đến logarit tự nhiên, ln, và nó phụ thuộc vào một hằng số (xác định hình dạng của đường cong) và vào thời gian. Nó cung cấp một mô hình để mô tả các quá trình như phân rã phóng xạ.
Nếu một phân phối mũ là một giả định hợp lý cho hình dạng của một đường cong sống còn, thì công thức sau có thể được sử dụng để ước tính tỷ lệ nguy cơ, được ký hiệu bằng chữ H, khi có các quan sát bị kiểm duyệt xảy ra:
trong đó d là số ca tử vong, là tổng thời gian thất bại, và là tổng thời gian bị kiểm duyệt. Việc tính toán tỷ lệ nguy cơ đòi hỏi chúng ta phải cộng tất cả các thời gian thất bại và thời gian bị kiểm duyệt.
Một lý do mà tỷ lệ nguy cơ được quan tâm là vì nghịch đảo của nó là một ước tính của thời gian sống còn trung bình. Các công thức rất phức tạp, và may mắn thay, các chương trình máy tính tính toán hàm nguy cơ và khoảng tin cậy 95% của nó như một phần của phân tích Kaplan-Meier.
NGUYÊN TẮC PHÂN TÍCH THEO Ý ĐỊNH ĐIỀU TRỊ (INTENTION-TO-TREAT)
Trong phần phương pháp của các bài báo khoa học báo cáo kết quả thử nghiệm lâm sàng, các nhà điều tra thường tuyên bố rằng họ đã phân tích dữ liệu trên cơ sở phân tích theo ý định điều trị (intention-to-treat – ITT). Ví dụ, trong một nghiên cứu về hiệu quả của một chương trình phòng chống tiểu đường 16 tuần (DPP), Ciemins và cộng sự (2018) đã sử dụng phương pháp phân tích theo ý định điều trị. Các biến kết cục chính trong nghiên cứu này là giảm cân, đạt được mục tiêu hoạt động thể chất, và đạt được mục tiêu gram chất béo hàng ngày.
Trong phần phương pháp, các nhà nghiên cứu tuyên bố: “Mục tiêu chính của phân tích ITT này là để xác định xem một can thiệp được cung cấp đồng thời cho nhiều cộng đồng qua telehealth có mang lại kết quả lâm sàng tương đương với một can thiệp được cung cấp trực tiếp hay không. Là một phân tích ITT, tất cả các bệnh nhân được ghi danh vào nghiên cứu đều được bao gồm trong phân tích, bất kể sự tham dự…” Tuyên bố này có nghĩa là kết quả của mỗi bệnh nhân tham gia thử nghiệm đã được bao gồm trong phân tích của nhóm mà bệnh nhân được phân ngẫu nhiên, bất kể các sự kiện xảy ra sau đó. Trong nghiên cứu của Ciemens và đồng nghiệp (2018), việc phân ngẫu nhiên dựa trên vị trí nông thôn hoặc thành thị của các đối tượng.
Phân tích dữ liệu trên cơ sở ý định điều trị là phù hợp vì nhiều lý do. Thứ nhất là vấn đề bỏ cuộc, như trong nghiên cứu của Ciemens và đồng nghiệp (2018). Cách tiếp cận ITT là phù hợp cho nghiên cứu này vì việc người tham gia các chương trình DPP bỏ cuộc tại một thời điểm nào đó là điều tự nhiên và do đó ITT cũng đánh giá tác động của những người bỏ cuộc. Có khả năng những bệnh nhân bỏ cuộc khỏi nhóm điều trị có một số đặc điểm mà, độc lập với việc điều trị, có thể ảnh hưởng đến kết quả không? Giả sử, ví dụ, những đối tượng bỏ cuộc khỏi nghiên cứu có chỉ số BMI cao hơn những người ở lại nghiên cứu. Những đối tượng có chỉ số BMI ban đầu cao hơn có thể có tiềm năng giảm cân nhiều hơn trong chương trình. Nếu những bệnh nhân này bị bỏ qua khỏi phân tích, kết quả có thể có vẻ tốt hơn cho nhóm nông thôn hoặc thành thị so với thực tế; tức là, kết quả bị sai lệch. Mặc dù không có dấu hiệu nào cho thấy điều này đã xảy ra trong nghiên cứu này, nhưng dễ dàng thấy được các sự kiện như vậy có thể ảnh hưởng đến kết luận như thế nào, và các nhà điều tra này đã đúng khi phân tích dữ liệu trên cơ sở ý định điều trị.
Nguyên tắc ý định điều trị cũng quan trọng trong các nghiên cứu mà bệnh nhân chuyển đổi (cross over) từ nhóm điều trị này sang nhóm điều trị khác. Ví dụ, Nghiên cứu Phẫu thuật Động mạch Vành (CASS, 1983) kinh điển là một thử nghiệm ngẫu nhiên về phẫu thuật bắc cầu động mạch vành. Bệnh nhân được phân vào nhóm điều trị nội khoa hoặc can thiệp phẫu thuật để đánh giá hiệu quả của việc điều trị đối với các kết cục của bệnh nhân mắc bệnh động mạch vành. Như trong nhiều nghiên cứu so sánh một phương pháp điều trị bảo tồn với một can thiệp tích cực hơn, một số bệnh nhân trong nghiên cứu CASS được phân ngẫu nhiên vào nhóm điều trị nội khoa sau đó đã trải qua phẫu thuật. Và, một số bệnh nhân được phân ngẫu nhiên vào nhóm phẫu thuật lại được điều trị nội khoa.
Vấn đề với các nghiên cứu mà bệnh nhân chuyển đổi từ một phương pháp điều trị sang phương pháp khác là chúng ta không biết tại sao sự chuyển đổi lại xảy ra. Có phải một số bệnh nhân ban đầu được phân vào nhóm điều trị nội khoa đã cải thiện đến mức họ trở thành ứng cử viên cho phẫu thuật không? Nếu vậy, điều này có thể làm cho kết quả trong nhóm phẫu thuật có vẻ tốt hơn so với thực tế (bởi vì những bệnh nhân “khỏe mạnh hơn” đã được loại bỏ khỏi nhóm nội khoa và chuyển sang nhóm phẫu thuật). Mặt khác, có lẽ tình trạng của những bệnh nhân ban đầu được phân vào nhóm điều trị nội khoa đã xấu đi đến mức bệnh nhân hoặc gia đình nhất quyết yêu cầu phẫu thuật. Nếu vậy, điều này có thể làm cho kết quả của nhóm phẫu thuật có vẻ tồi tệ hơn so với thực tế (bởi vì những bệnh nhân “bệnh nặng hơn” đã được chuyển từ nhóm nội khoa sang nhóm phẫu thuật). Vấn đề là, chúng ta không biết tại sao bệnh nhân lại chuyển đổi, và các nhà điều tra cũng vậy.
Trong quá khứ, một số nhà điều tra trình bày các nghiên cứu với tình huống như vậy đã phân tích bệnh nhân theo nhóm họ thuộc về vào cuối nghiên cứu. Các nhà nghiên cứu khác đã loại bỏ khỏi phân tích bất kỳ bệnh nhân nào đã chuyển đổi. Dễ dàng thấy tại sao cả hai cách tiếp cận này đều có khả năng gây sai lệch. Cách tiếp cận tốt nhất, được các nhà thống kê sinh học và những người ủng hộ y học dựa trên bằng chứng khuyến nghị, là thực hiện tất cả các phân tích trên các nhóm ban đầu mà bệnh nhân đã được phân ngẫu nhiên. Nghiên cứu CASS đã diễn ra vài năm trước, và vào thời điểm đó không có sự đồng thuận nào về cách tốt nhất để phân tích các phát hiện. Do đó, các nhà điều tra CASS đã thực hiện các phân tích theo nhiều cách: theo nhóm ban đầu (ý định điều trị), theo các nhóm cuối cùng của nghiên cứu, và bằng cách loại bỏ tất cả các trường hợp chuyển đổi khỏi phân tích. Tất cả các phương pháp này đều cho cùng một kết quả, cụ thể là không có sự khác biệt về tỷ lệ sống còn, mặc dù các nghiên cứu sau này đã cho thấy sự khác biệt về các chỉ số chất lượng cuộc sống.
Nguyên tắc ý định điều trị áp dụng cho các nghiên cứu khác ngoài những nghiên cứu có sự sống còn là kết cục. Tuy nhiên, chúng tôi đã bao gồm chủ đề này ở đây vì nó rất phù hợp với các nghiên cứu sống còn.
TÓM TẮT
Cần có các phương pháp đặc biệt để phân tích dữ liệu từ các nghiên cứu về thời gian sống còn vì các quan sát bị kiểm duyệt xảy ra khi bệnh nhân tham gia vào các thời điểm khác nhau và ở lại trong một nghiên cứu trong các khoảng thời gian khác nhau. Nếu không, các nhà điều tra sẽ phải đợi cho đến khi tất cả các đối tượng đã tham gia nghiên cứu trong một khoảng thời gian nhất định trước khi phân tích dữ liệu. Trong y học, các đường cong sống còn thường được vẽ bằng phương pháp giới hạn tích Kaplan-Meier và, ít thường xuyên hơn, là phương pháp tính toán bảo hiểm (bảng sống).
Trong nghiên cứu của Lin và cộng sự (2018), có sự khác biệt thống kê trong đường cong sống còn toàn bộ () đối với bệnh nhân chỉ dùng regorafenib so với điều trị kết hợp. Sự khác biệt này cùng với các đường cong Kaplan-Meier đã được báo cáo trong bài báo.
Chúng tôi đã minh họa các phương pháp Kaplan-Meier và tính toán bảo hiểm cho thời gian sống còn. Phương pháp Kaplan-Meier tính toán sự sống còn mỗi khi một bệnh nhân qua đời và cung cấp các ước tính chính xác. Mặc dù thường tốn nhiều thời gian hơn để tính toán, việc sử dụng rộng rãi máy tính đã làm cho đường cong Kaplan-Meier trở thành quy trình được lựa chọn.
Chúng tôi đã kết thúc chương với một cuộc thảo luận về nguyên tắc quan trọng của phân tích theo ý định điều trị, theo đó bệnh nhân được phân tích trong nhóm mà họ đã được phân công ban đầu. Chúng tôi đã mô tả một số vấn đề trong việc giải thích kết quả khi nguyên tắc này không được tuân thủ, và chúng tôi đã chỉ ra khả năng áp dụng của nguyên tắc ý định điều trị cho bất kỳ nghiên cứu nào, bất kể kết cục là sự sống còn hay một biến số khác.
BÀI TẬP THỰC HÀNH
- Một bác sĩ phẫu thuật ghép thận đã so sánh hai nhóm bệnh nhân được ghép thận. Một nhóm đã trải qua cấy ghép và nhận azathioprine để làm chậm quá trình thải ghép của cơ quan được cấy ghép. Nhóm còn lại được điều trị bằng cyclosporine, một chất điều hòa miễn dịch. Dữ liệu về hai nhóm này được cung cấp trong Bảng 9-8 và Bảng 9-9. a. Thực hiện các tính toán cho đường cong sống còn Kaplan-Meier. b. Vẽ các đường cong sống còn. Bạn có nghĩ rằng các đường cong sống còn khác biệt đáng kể không? c. Thực hiện phép kiểm logrank và giải thích kết quả.
- Kasurinen và cộng sự (2018) muốn xác định xem mức độ MMP-14 huyết thanh có ảnh hưởng đến sự sống còn của bệnh nhân ung thư dạ dày hay không. Sử dụng dữ liệu để so sánh sự sống còn của bệnh nhân có MMP-14 huyết thanh lớn hơn 0,0729 (được các tác giả coi là cao) với những người có mức MMP-14 thấp hơn. a. Mức MMP-14 huyết thanh nào dẫn đến thời gian sống còn dài hơn? Liệu sự sống còn dài hơn có được duy trì trong một thời gian dài không? b. Giá trị của thống kê logrank là bao nhiêu? Bạn kết luận gì từ giá trị này? c. Các sai lệch tiềm ẩn trong việc đưa ra kết luận về phương pháp điều trị trong nghiên cứu này là gì?
- Tham khảo Hình 9-5, minh họa các đường cong sống còn cho bệnh nhân được phân loại theo phương pháp điều trị (Lin và cộng sự, 2018). Có thể tìm thấy thời gian sống còn trung vị cho hai nhóm không? Nếu có, thời gian sống còn trung vị là bao nhiêu?
- Kasurinen và cộng sự (2018) cũng phân loại bệnh nhân theo phân loại Laurén (1 = ruột, 2 = lan tỏa). Sử dụng cùng bệnh nhân có giá trị MMP-14 được sử dụng trong Bài tập 2. a. Sử dụng dữ liệu đã tải xuống trước đó về các đường cong Kaplan-Meier cho số năm sống còn của bệnh nhân ung thư dạng ruột và lan tỏa. b. Dựa trên biểu đồ, bạn sẽ kết luận gì về phân loại nguy cơ được sử dụng trong nghiên cứu?
- Tham khảo nghiên cứu MRFIT đã được thảo luận trong Chương 8 và được sử dụng làm bài tập nhóm trong chương đó. Tham khảo Hình 9-2 trong nghiên cứu: bệnh tim mạch vành tích lũy và tỷ lệ tử vong toàn bộ cho hai nhóm. Phương pháp thống kê nào là tối ưu để xác định xem hai nhóm có khác nhau ở một trong hai kết cục này không?
- Kết quả trong một đoàn hệ bệnh nhân đã phẫu thuật bắc cầu động mạch vành 20 năm trước đã được Lawrie và đồng nghiệp (1991) mô tả. Các hoạt động theo dõi bao gồm các cuộc hẹn với bác sĩ, bảng câu hỏi và các cuộc phỏng vấn qua điện thoại định kỳ. Dữ liệu có sẵn trên 92% bệnh nhân 20 năm sau phẫu thuật. Các nhà điều tra đã kiểm tra sự sống còn cho một số phân nhóm và sử dụng sự sống còn kỳ vọng cho dân số được điều chỉnh theo tuổi và giới tính từ điều tra dân số Hoa Kỳ để cung cấp một đường cơ sở. Các đường cong được tính toán bằng phương pháp Kaplan-Meier; các nhóm được xác định bởi mạch máu liên quan được đưa ra trong Hình 9-6. Điều quan trọng cần nhận ra là các quy trình phẫu thuật bắc cầu động mạch vành đã thay đổi rất nhiều kể từ thời điểm của nghiên cứu này, và bệnh nhân ngày nay có kết quả dài hạn thuận lợi hơn. a. Nhóm nào có tỷ lệ sống còn tốt nhất? b. Nhóm nào có tỷ lệ tử vong cao nhất? c. Thời gian sống còn trung vị gần đúng trong mỗi nhóm là bao nhiêu?
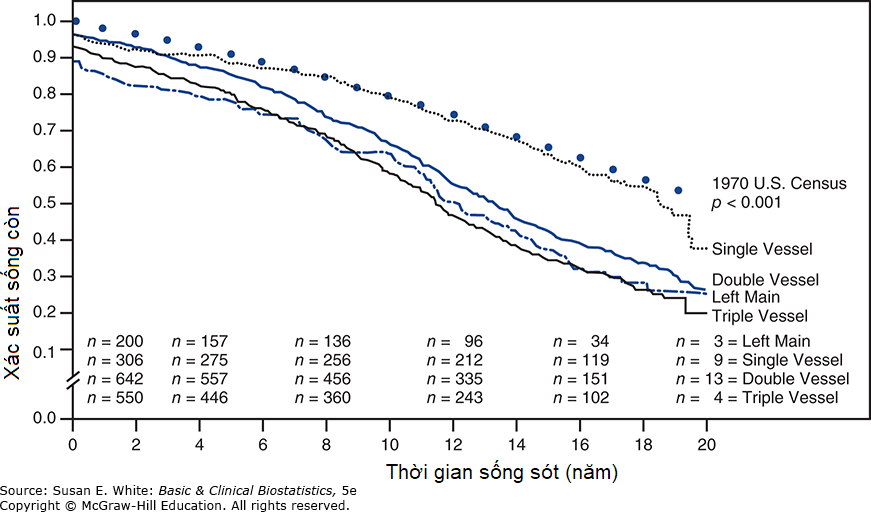
Hình 9-6. Xác suất sống còn cho 1698 bệnh nhân theo mức độ bệnh động mạch vành trước phẫu thuật.
Bảng 9-8. Sự sống còn của thận ở bệnh nhân được ghép và nhận azathioprine.
| Bệnh nhân | Ngày ghép | Số tháng trong nghiên cứu | Thất bại (1=có, 0=kiểm duyệt) |
|---|---|---|---|
| 1 | 11-1-1978 | 2 | 1 |
| 2 | 18-1-1978 | 23 | 0 |
| 3 | 29-1-1978 | 23 | 0 |
| 4 | 4-4-1978 | 1 | 1 |
| 5 | 19-4-1978 | 20 | 0 |
| 6 | 10-5-1978 | 19 | 0 |
| 7 | 14-5-1978 | 3 | 1 |
| 8 | 21-5-1978 | 5 | 1 |
| 9 | 6-6-1978 | 17 | 1 |
| 10 | 17-6-1978 | 18 | 0 |
| 11 | 21-6-1978 | 18 | 0 |
| 12 | 22-7-1978 | 3 | 1 |
| 13 | 27-9-1978 | 15 | 0 |
| 14 | 5-10-1978 | 3 | 1 |
| 15 | 22-10-1978 | 14 | 0 |
| 16 | 15-11-1978 | 13 | 0 |
| 17 | 6-12-1978 | 12 | 0 |
| 18 | 12-12-1978 | 12 | 0 |
| 19 | 1-2-1979 | 10 | 0 |
| 20 | 16-2-1979 | 10 | 0 |
| 21 | 8-4-1979 | 8 | 0 |
| 22 | 11-4-1979 | 8 | 0 |
| 23 | 18-4-1979 | 8 | 0 |
| 24 | 26-6-1979 | 1 | 1 |
| 25 | 3-7-1979 | 5 | 0 |
| 26 | 12-7-1979 | 5 | 0 |
| 27 | 18-7-1979 | 1 | 1 |
| 28 | 23-8-1979 | 4 | 0 |
| 29 | 16-10-1979 | 2 | 0 |
| 30 | 12-12-1979 | 1 | 0 |
| 31 | 24-12-1979 | 1 | 0 |
| Dữ liệu từ Dr. A. Birtch. | |||
Bảng 9-9. Sự sống còn của thận ở bệnh nhân được ghép và nhận cyclosporine.
| Bệnh nhân | Ngày ghép | Số tháng trong nghiên cứu | Thất bại (1=có, 0=kiểm duyệt) |
|---|---|---|---|
| 1 | 8-2-1984 | 22 | 0 |
| 2 | 22-2-1984 | 22 | 0 |
| 3 | 25-2-1984 | 22 | 0 |
| 4 | 29-2-1984 | 8 | 1 |
| 5 | 12-3-1984 | 21 | 0 |
| 6 | 22-3-1984 | 1 | 1 |
| 7 | 26-4-1984 | 20 | 0 |
| 8 | 2-5-1984 | 19 | 0 |
| 9 | 9-5-1984 | 19 | 0 |
| 10 | 6-6-1984 | 18 | 0 |
| 11 | 11-7-1984 | 17 | 0 |
| 12 | 20-7-1984 | 17 | 0 |
| 13 | 18-8-1984 | 16 | 0 |
| 14 | 5-9-1984 | 15 | 0 |
| 15 | 15-9-1984 | 15 | 0 |
| 16 | 3-10-1984 | 14 | 0 |
| 17 | 9-11-1984 | 13 | 0 |
| 18 | 27-11-1984 | 6 | 1 |
| 19 | 5-12-1984 | 12 |
0 |
| 20 | 6-12-1984 | 12 | 0 |
| 21 | 19-12-1984 | 12 | 0 |
| Dữ liệu từ Dr. A. Birtch. | |||
Bảng Chú giải Thuật ngữ Thống kê Anh – Việt (Chương 9)
| STT | Thuật ngữ tiếng Anh |
Phiên âm |
Nghĩa tiếng Việt |
|---|---|---|---|
| 1 | Survival | /sərˈvaɪvəl/ | Sự sống còn, Thời gian sống còn |
| 2 | Recurrence | /rɪˈkɜːrəns/ | Sự tái phát |
| 3 | Outcome | /ˈaʊtkʌm/ | Kết cục (Kết quả cuối cùng của một bệnh hoặc điều trị) |
| 4 | Censored | /ˈsensərd/ | Bị kiểm duyệt (Dữ liệu chưa hoàn chỉnh, ví dụ: bệnh nhân vẫn còn sống khi kết thúc nghiên cứu) |
| 5 | Doubly censored | /ˈdʌbli ˈsensərd/ | Bị kiểm duyệt kép (Bệnh nhân tham gia và kết thúc nghiên cứu tại các thời điểm khác nhau) |
| 6 | Life table methods | /laɪf ˈteɪbəl ˈmeθədz/ | Phương pháp bảng sống |
| 7 | Actuarial methods | /ˌækʧuˈeriəl ˈmeθədz/ | Phương pháp tính toán bảo hiểm |
| 8 | Survival curves | /sərˈvaɪvəl kɜːrvz/ | Đường cong sống còn |
| 9 | Kaplan-Meier curves | /ˈkæplən ˈmaɪər kɜːrvz/ | Đường cong Kaplan-Meier |
| 10 | Survival analysis | /sərˈvaɪvəl əˈnæləsɪs/ | Phân tích sống còn |
| 11 | Logrank statistic | /ˈlɔːɡræŋk stəˈtɪstɪk/ | Thống kê Logrank |
| 12 | Hazard ratio | /ˈhæzərd ˈreɪʃiəʊ/ | Tỷ số nguy cơ |
| 13 | Odds ratio | /ɒdz ˈreɪʃiəʊ/ | Tỷ số chênh |
| 14 | Mantel-Haenszel statistic | /ˈmæntəl ˈhɛnzəl stəˈtɪstɪk/ | Thống kê Mantel-Haenszel |
| 15 | Hazard function | /ˈhæzərd ˈfʌŋkʃən/ | Hàm nguy cơ |
| 16 | Intention-to-treat principle | /ɪnˈtenʃən tu triːt ˈprɪnsəpəl/ | Nguyên tắc phân tích theo ý định điều trị (ITT) |
| 17 | Mortality | /mɔːrˈtæləti/ | Tỷ lệ tử vong |
| 18 | Morbidity | /mɔːrˈbɪdəti/ | Tỷ lệ mắc bệnh |
| 19 | Censored observations | /ˈsensərd ˌɒbzərˈveɪʃənz/ | Các quan sát bị kiểm duyệt |
| 20 | Progressively censored | /prəˈɡresɪvli ˈsensərd/ | Bị kiểm duyệt lũy tiến |
| 21 | Actuarial analysis | /ˌækʧuˈeriəl əˈnæləsɪs/ | Phân tích tính toán bảo hiểm |
| 22 | Life table analysis | /laɪf ˈteɪbəl əˈnæləsɪs/ | Phân tích bảng sống |
| 23 | Cross-sectional data | /krɒs ˈsekʃənəl ˈdeɪtə/ | Dữ liệu cắt ngang |
| 24 | Current life table | /ˈkɜːrənt laɪf ˈteɪbəl/ | Bảng sống hiện tại |
| 25 | Cohort life tables | /ˈkəʊhɔːrt laɪf ˈteɪbəlz/ | Bảng sống đoàn hệ |
| 26 | Cohort studies | /ˈkəʊhɔːrt ˈstʌdiz/ | Nghiên cứu đoàn hệ |
| 27 | Prospective | /prəˈspektɪv/ | Tiến cứu |
| 28 | Historical (Retrospective) | /hɪˈstɒrɪkəl/ | Hồi cứu |
| 29 | Clinical trials | /ˈklɪnɪkəl ˈtraɪəlz/ | Thử nghiệm lâm sàng |
| 30 | Mean length of time | /miːn leŋθ əv taɪm/ | Thời gian trung bình |
| 31 | Mean survival time | /miːn sərˈvaɪvəl taɪm/ | Thời gian sống còn trung bình |
| 32 | Median length of survival | /ˈmiːdiən leŋθ əv sərˈvaɪvəl/ | Thời gian sống còn trung vị |
| 33 | Person-years of observation | /ˈpɜːrsən jɪərz əv ˌɒbzərˈveɪʃən/ | Người-năm quan sát |
| 34 | Mortality rates | /mɔːrˈtæləti reɪts/ | Tỷ suất tử vong |
| 35 | 3- and 5-year survival | /θriː ənd faɪv jɪər sərˈvaɪvəl/ | Tỷ lệ sống còn 3 năm và 5 năm |
| 36 | Cutler-Ederer method | /ˈkʌtlər ˈiːdərər ˈmeθəd/ | Phương pháp Cutler-Ederer |
| 37 | Time intervals | /taɪm ˈɪntərvəlz/ | Các khoảng thời gian |
| 38 | Terminal event | /ˈtɜːrmɪnəl ɪˈvent/ | Biến cố kết thúc (thường là tử vong) |
| 39 | Withdrawals | /wɪðˈdrɔːəlz/ | Các trường hợp rút lui |
| 40 | Number exposed to risk | /ˈnʌmbər ɪkˈspoʊzd tu rɪsk/ | Số người chịu rủi ro |
| 41 | Proportion terminating | /prəˈpɔːrʃən ˈtɜːrmɪneɪtɪŋ/ | Tỷ lệ kết thúc |
| 42 | Proportion surviving | /prəˈpɔːrʃən sərˈvaɪvɪŋ/ | Tỷ lệ sống sót |
| 43 | Cumulative proportion survival | /ˈkjuːmjələtɪv prəˈpɔːrʃən sərˈvaɪvəl/ | Tỷ lệ sống sót tích lũy |
| 44 | Conditional probability | /kənˈdɪʃənəl ˌprɒbəˈbɪləti/ | Xác suất có điều kiện |
| 45 | Survival function | /sərˈvaɪvəl ˈfʌŋkʃən/ | Hàm sống còn |
| 46 | Kaplan-Meier product limit method | /ˈkæplən ˈmaɪər ˈprɒdʌkt ˈlɪmɪt ˈmeθəd/ | Phương pháp giới hạn tích Kaplan-Meier |
| 47 | Event Time | /ɪˈvent taɪm/ | Thời gian xảy ra biến cố |
| 48 | Number at Risk | /ˈnʌmbər æt rɪsk/ | Số người có nguy cơ |
| 49 | Number of Events | /ˈnʌmbər əv ɪˈvents/ | Số biến cố |
| 50 | Standard deviation | /ˈstændərd ˌdiːviˈeɪʃən/ | Độ lệch chuẩn |
| 51 | Confidence bands | /ˈkɒnfɪdəns bændz/ | Dải tin cậy (Khoảng tin cậy cho toàn bộ đường cong) |
| 52 | Standard error | /ˈstændərd ˈerər/ | Sai số chuẩn |
| 53 | Cumulative survival estimate | /ˈkjuːmjələtɪv sərˈvaɪvəl ˈestɪmət/ | Ước tính sống còn tích lũy |
| 54 | Comparing two survival curves | /kəmˈperɪŋ tuː sərˈvaɪvəl kɜːrvz/ | So sánh hai đường cong sống còn |
| 55 | Wilcoxon rank sum test | /wɪlˈkɒksən ræŋk sʌm test/ | Phép kiểm tổng hạng Wilcoxon |
| 56 | Independent-groups t-test | /ˌɪndɪˈpendənt ɡruːps ˈtiː test/ | Phép kiểm t cho các nhóm độc lập |
| 57 | Normally distributed | /ˈnɔːrməli dɪˈstrɪbjuːtɪd/ | Phân phối chuẩn |
| 58 | Positively skewed | /ˈpɒzətɪvli skjuːd/ | Lệch dương (Lệch phải) |
| 59 | Observed deaths | /əbˈzɜːrvd deθs/ | Số ca tử vong quan sát được |
| 60 | Expected deaths | /ɪkˈspektɪd deθs/ | Số ca tử vong kỳ vọng |
| 61 | Combined groups | /kəmˈbaɪnd ɡruːps/ | Các nhóm kết hợp |
| 62 | Chi-square test | /kaɪ skwer test/ | Phép kiểm Chi-bình phương |
| 63 | Significance | /sɪɡˈnɪfɪkəns/ | Mức ý nghĩa (thống kê) |
| 64 | Null hypothesis | /nʌl haɪˈpɒθəsɪs/ | Giả thuyết không |
| 65 | Survival distributions | /sərˈvaɪvəl ˌdɪstrɪˈbjuːʃənz/ | Các phân phối sống còn |
| 66 | Degrees of freedom | /dɪˈɡriːz əv ˈfriːdəm/ | Bậc tự do |
| 67 | Critical value | /ˈkrɪtɪkəl ˈvæljuː/ | Giá trị tới hạn |
| 68 | Statistically significant | /stəˈtɪstɪkli sɪɡˈnɪfɪkənt/ | Có ý nghĩa thống kê |
| 69 | Risk of mortality | /rɪsk əv mɔːrˈtæləti/ | Nguy cơ tử vong |
| 70 | Pooled odds ratio | /puːld ɒdz ˈreɪʃiəʊ/ | Tỷ số chênh gộp |
| 71 | Expected value | /ɪkˈspektɪd ˈvæljuː/ | Giá trị kỳ vọng |
| 72 | Variance | /ˈveriəns/ | Phương sai |
| 73 | Peto logrank test | /ˈpiːtoʊ ˈlɔːɡræŋk test/ | Phép kiểm logrank Peto |
| 74 | Gehan test | /ˈɡiːən test/ | Phép kiểm Gehan |
| 75 | Generalized Wilcoxon test | /ˈdʒenərəlaɪzd wɪlˈkɒksən test/ | Phép kiểm Wilcoxon tổng quát |
| 76 | Breslow test | /ˈbrezloʊ test/ | Phép kiểm Breslow |
| 77 | Generalized Kruskal-Wallis test | /ˈdʒenərəlaɪzd ˌkrʌskəl ˈwɒlɪs test/ | Phép kiểm Kruskal-Wallis tổng quát |
| 78 | Hazard rates | /ˈhæzərd reɪts/ | Tỷ suất nguy cơ |
| 79 | Constant hazard ratio | /ˈkɒnstənt ˈhæzərd ˈreɪʃiəʊ/ | Tỷ số nguy cơ không đổi |
| 80 | Proportional hazard rates | /prəˈpɔːrʃənəl ˈhæzərd reɪts/ | Tỷ suất nguy cơ tỷ lệ thuận |
| 81 | Cox’s proportional hazard model | /kɒksɪz prəˈpɔːrʃənəl ˈhæzərd ˈmɒdəl/ | Mô hình nguy cơ tỷ lệ thuận của Cox |
| 82 | Confounding variables | /kənˈfaʊndɪŋ ˈveriəbəlz/ | Các biến gây nhiễu |
| 83 | Conditional failure rate | /kənˈdɪʃənəl ˈfeɪljər reɪt/ | Tỷ lệ thất bại có điều kiện |
| 84 | Force of mortality | /fɔːrs əv mɔːrˈtæləti/ | Lực tử vong (thuật ngữ dịch tễ học cho hàm nguy cơ) |
| 85 | Exponential probability distribution | /ˌekspəˈnenʃəl ˌprɒbəˈbɪləti ˌdɪstrɪˈbjuːʃən/ | Phân phối xác suất mũ |
| 86 | Continuous distribution | /kənˈtɪnjuəs ˌdɪstrɪˈbjuːʃən/ | Phân phối liên tục |
| 87 | Natural logarithm | /ˈnæʧərəl ˈlɒɡərɪðəm/ | Logarit tự nhiên |
| 88 | Hazard rate | /ˈhæzərd reɪt/ | Tỷ suất nguy cơ |
| 89 | Failure times | /ˈfeɪljər taɪmz/ | Thời gian cho đến khi thất bại (biến cố xảy ra) |
| 90 | Censored times | /ˈsensərd taɪmz/ | Thời gian bị kiểm duyệt |
| 91 | Primary outcomes | /ˈpraɪmeri ˈaʊtkʌmz/ | Các kết cục chính |
| 92 | Randomization | /ˌrændəmaɪˈzeɪʃən/ | Phân nhóm ngẫu nhiên |
| 93 | Dropouts | /ˈdrɒpaʊts/ | Các trường hợp bỏ cuộc |
| 94 | Bias | /ˈbaɪəs/ | Sai lệch, Thiên kiến |
| 95 | Crossover | /ˈkrɒsəʊvər/ | Sự chuyển đổi (bệnh nhân chuyển từ nhóm điều trị này sang nhóm khác) |
| 96 | Randomized trial | /ˈrændəmaɪzd ˈtraɪəl/ | Thử nghiệm ngẫu nhiên |
| 97 | Medical treatment | /ˈmedɪkəl ˈtriːtmənt/ | Điều trị nội khoa |
| 98 | Surgical intervention | /ˈsɜːrdʒɪkəl ˌɪntərˈvenʃən/ | Can thiệp ngoại khoa |
| 99 | Evidence-based medicine | /ˈevɪdəns beɪst ˈmedɪsɪn/ | Y học dựa trên bằng chứng |
| 100 | Endpoints | /ˈendpɔɪnts/ | Các điểm cuối (các kết cục được đo lường trong nghiên cứu) |
